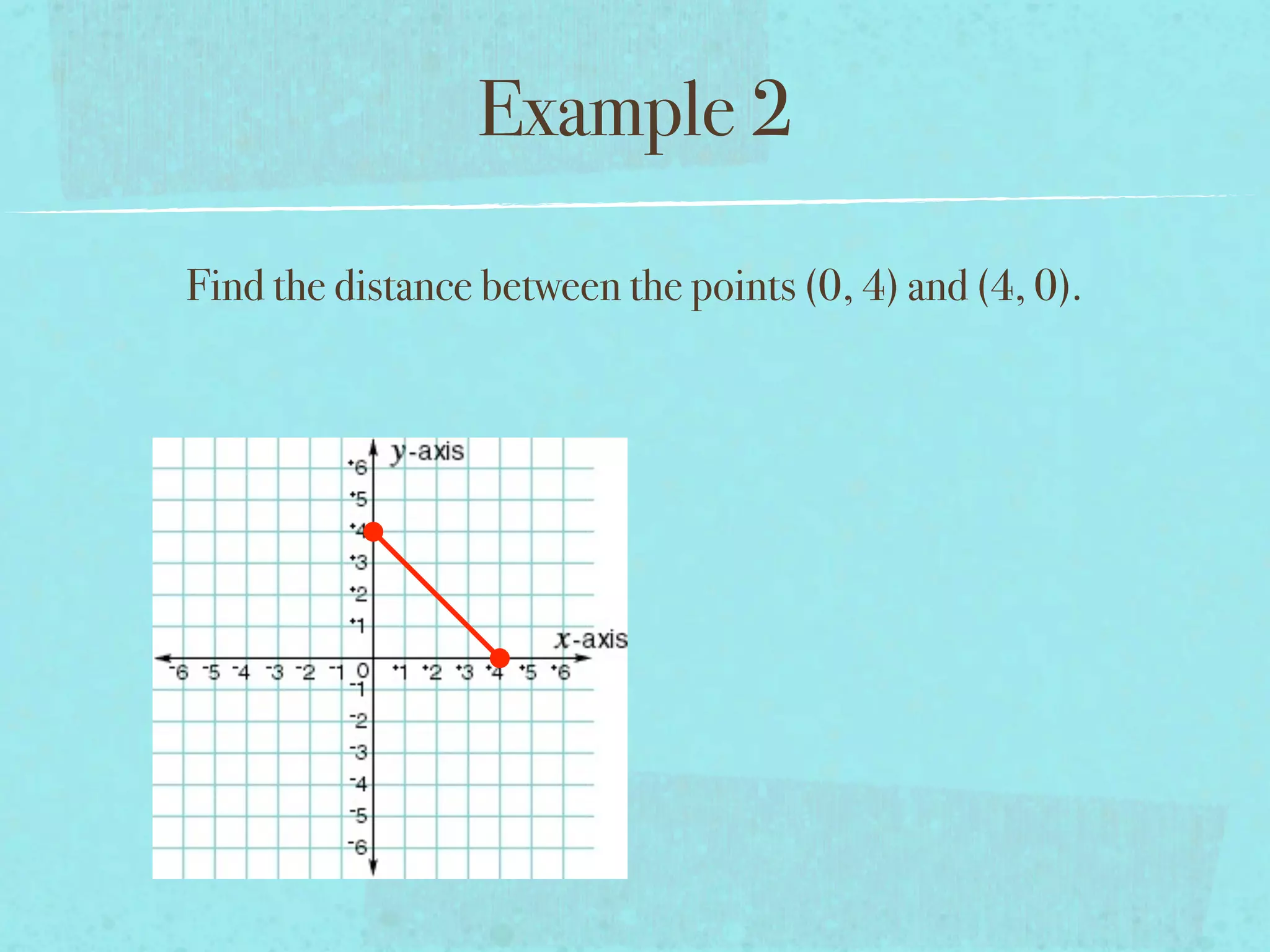
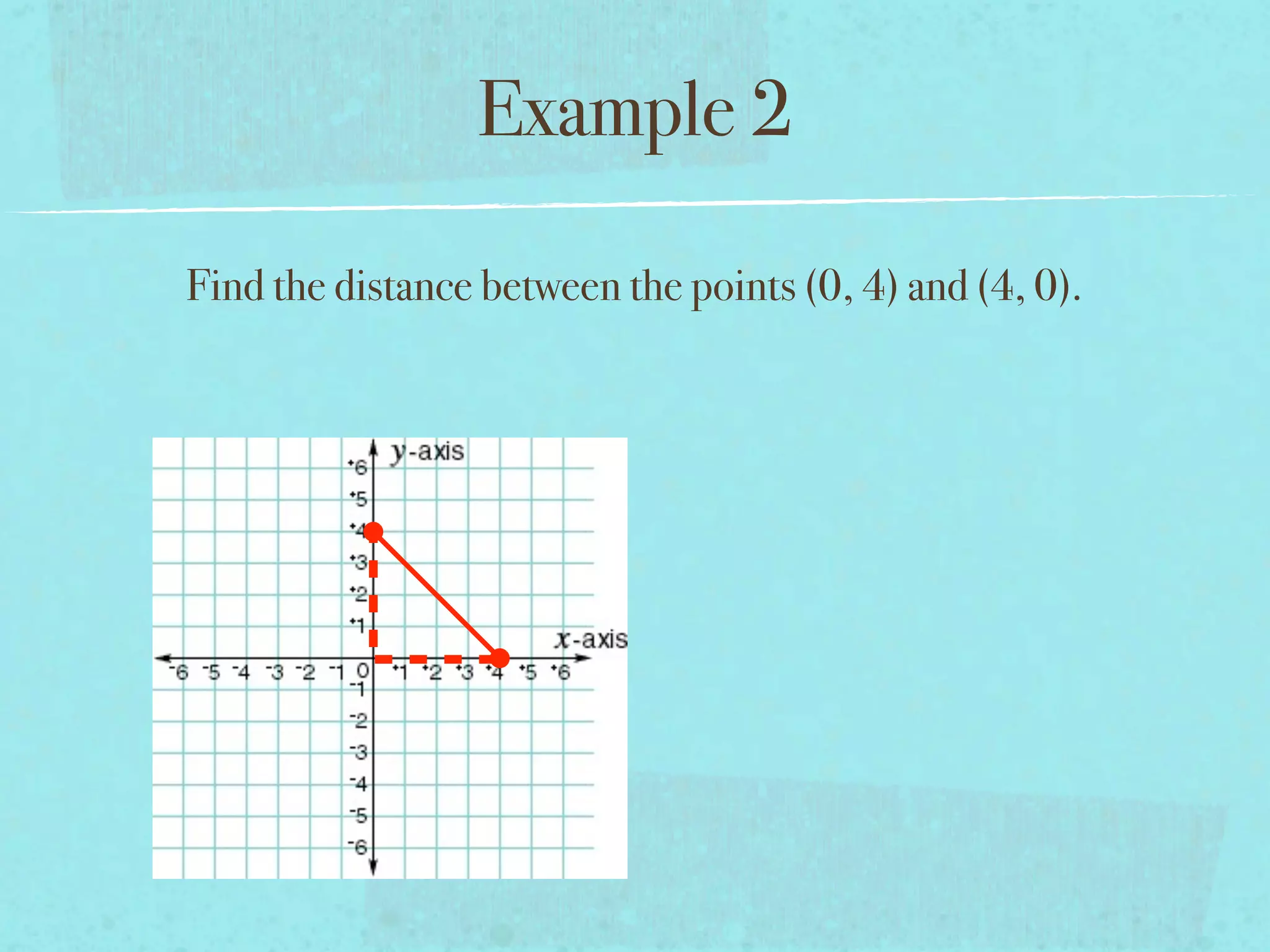
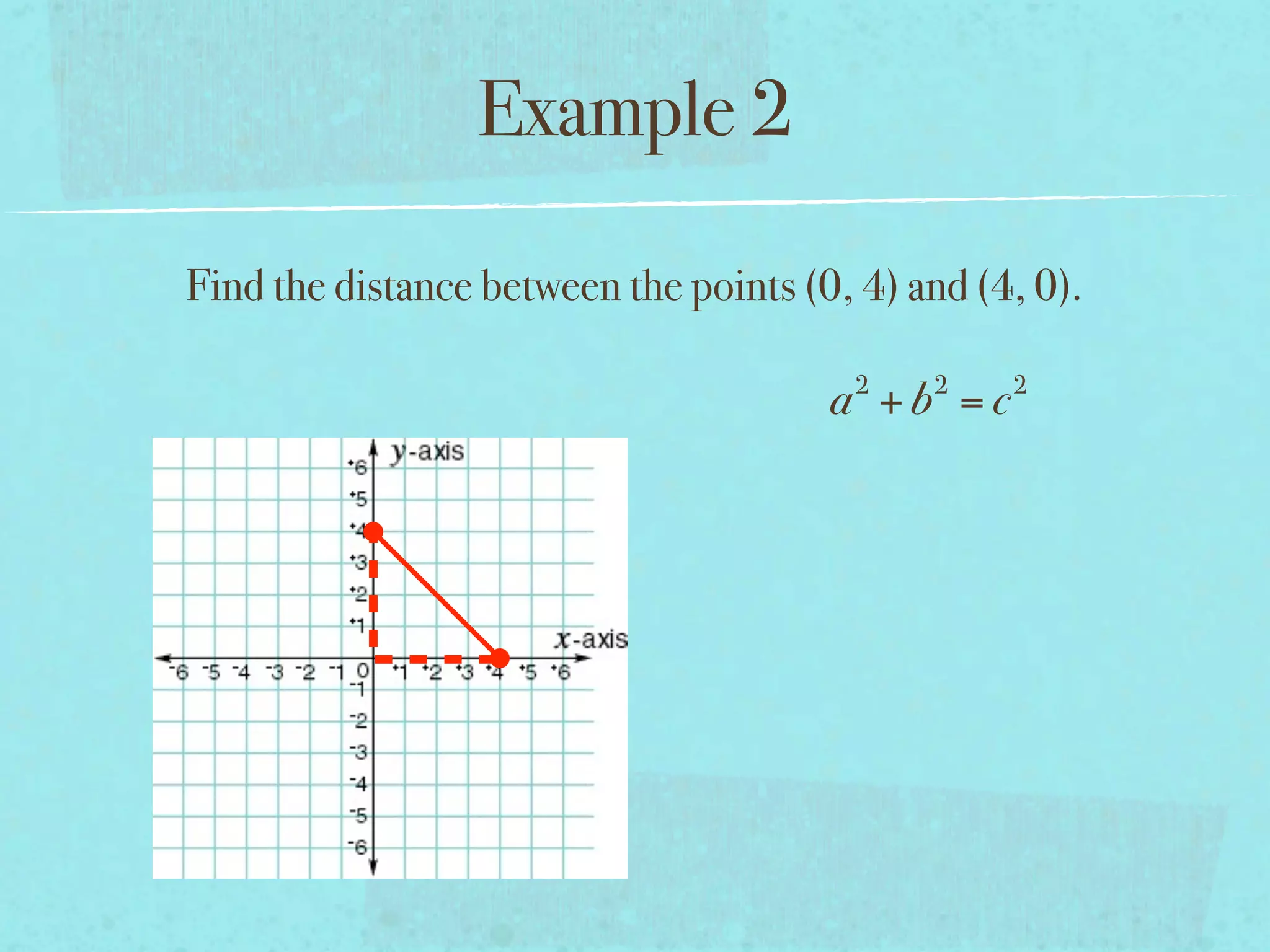
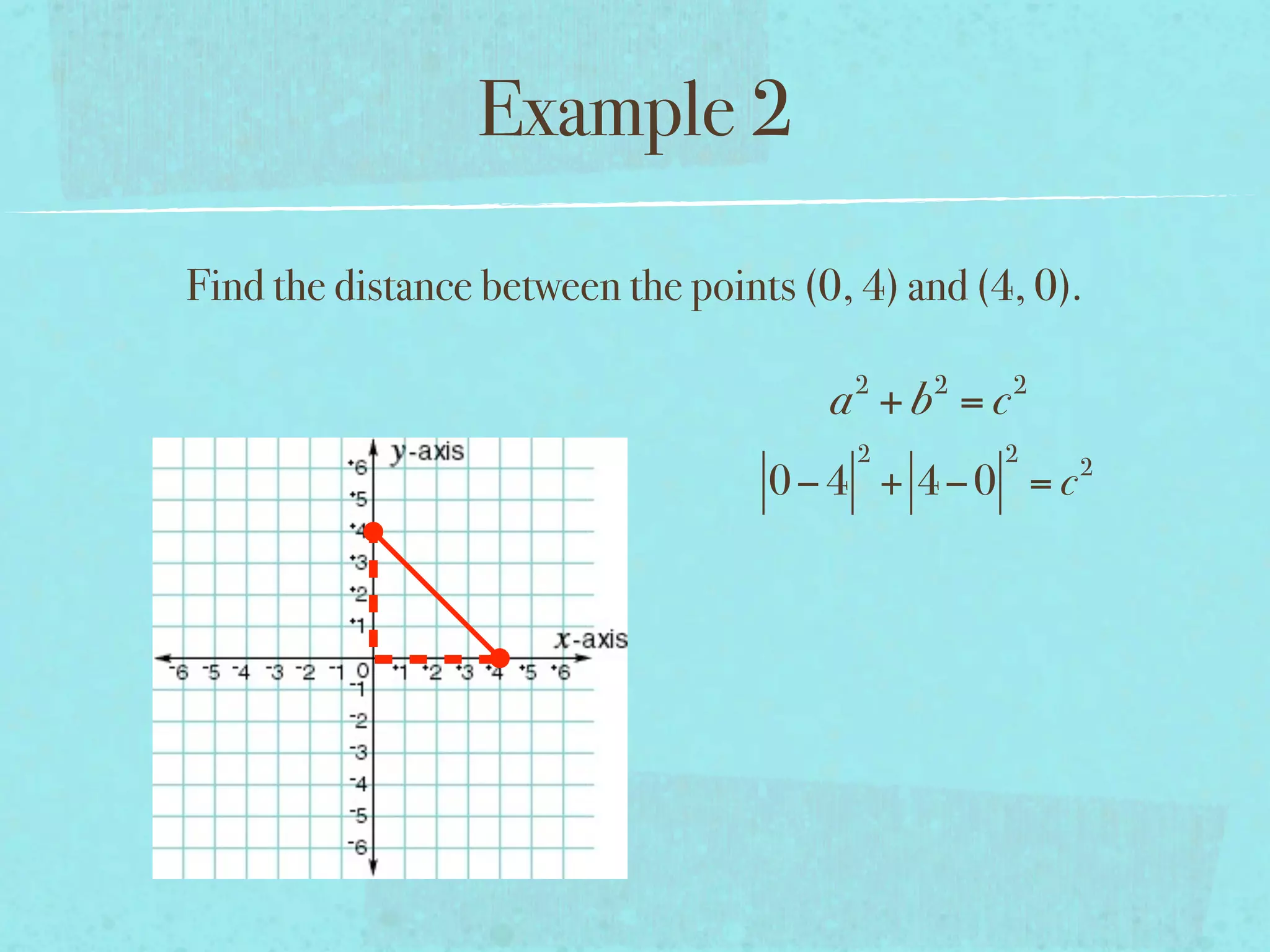
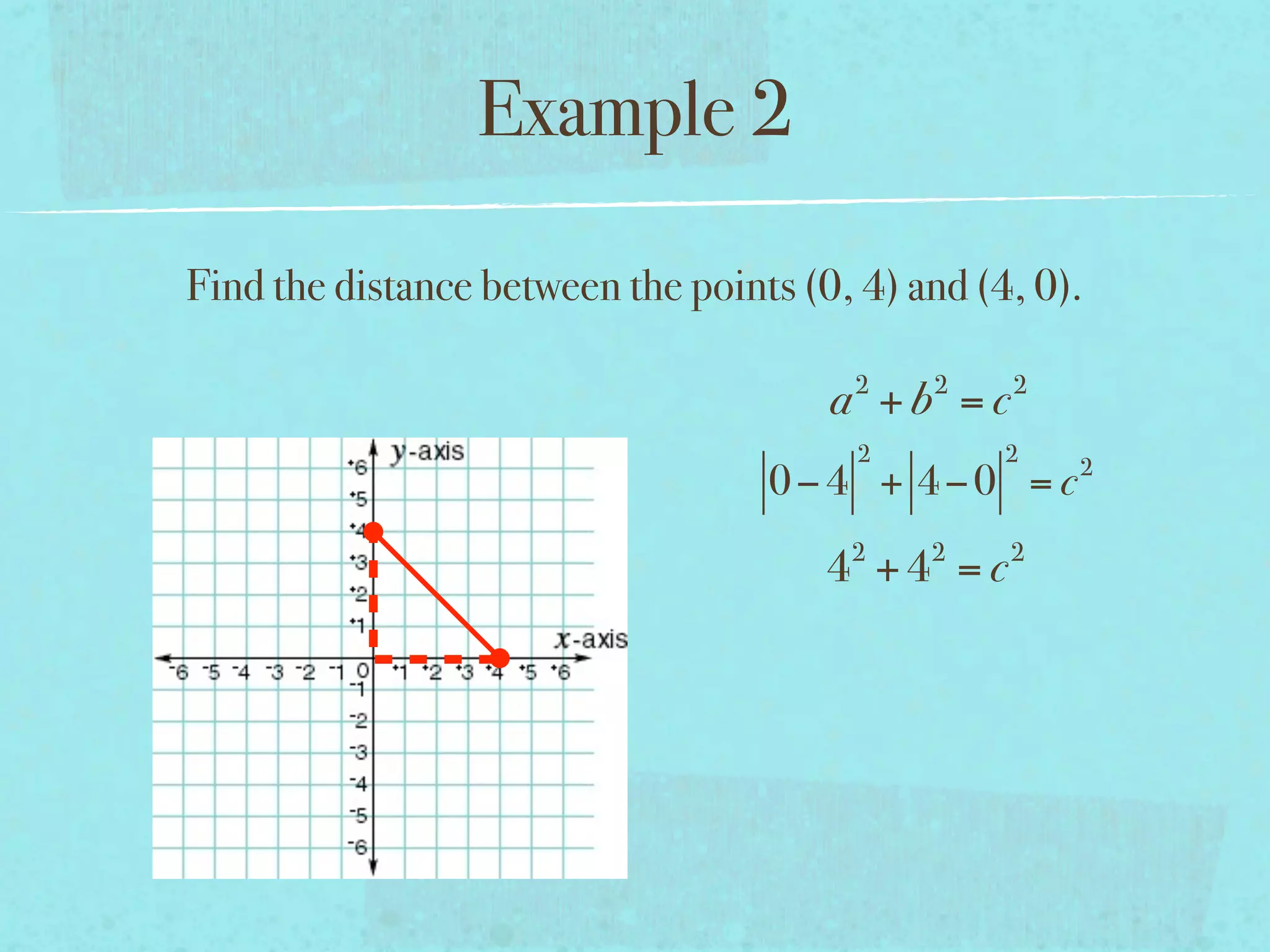
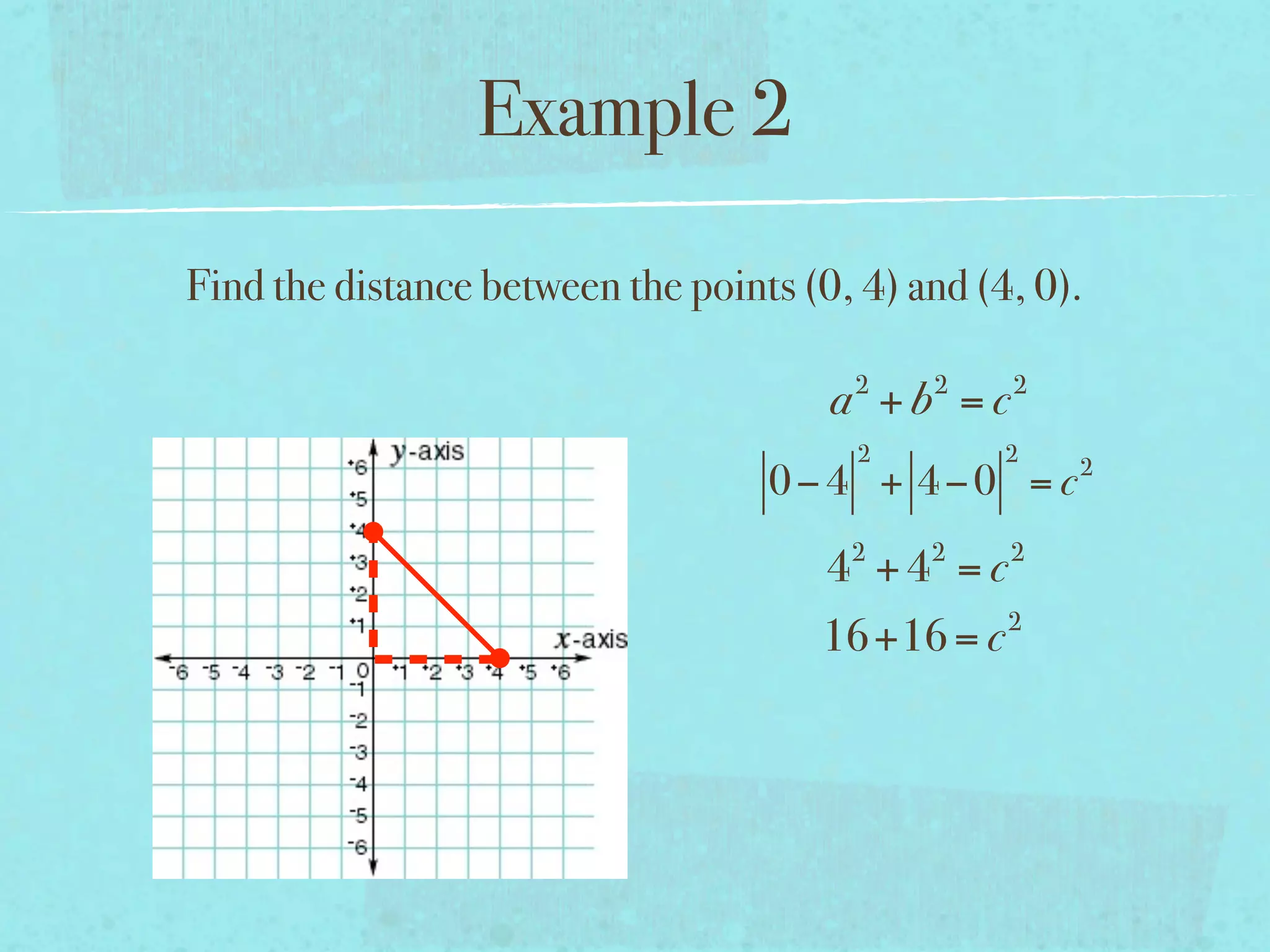
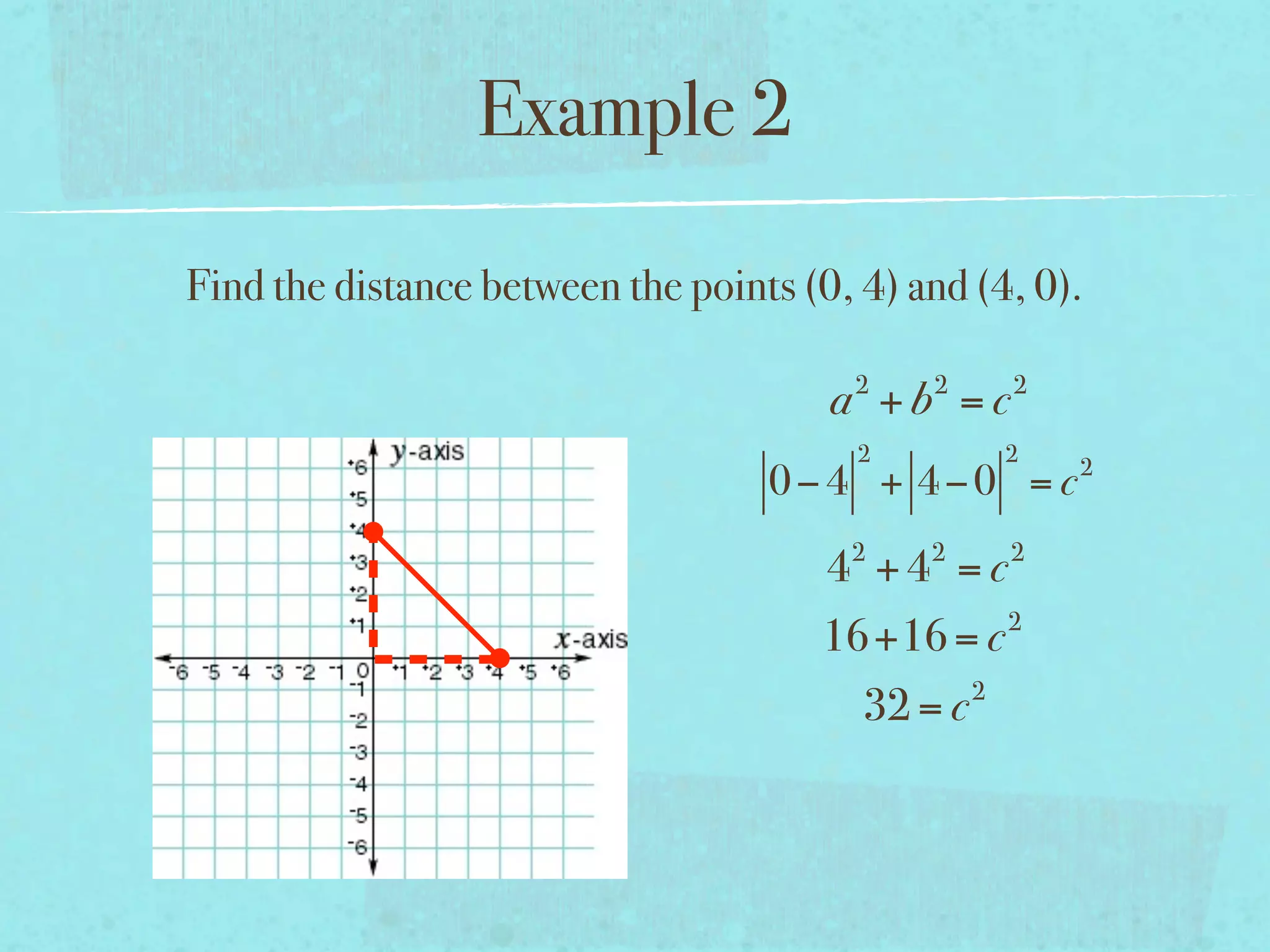
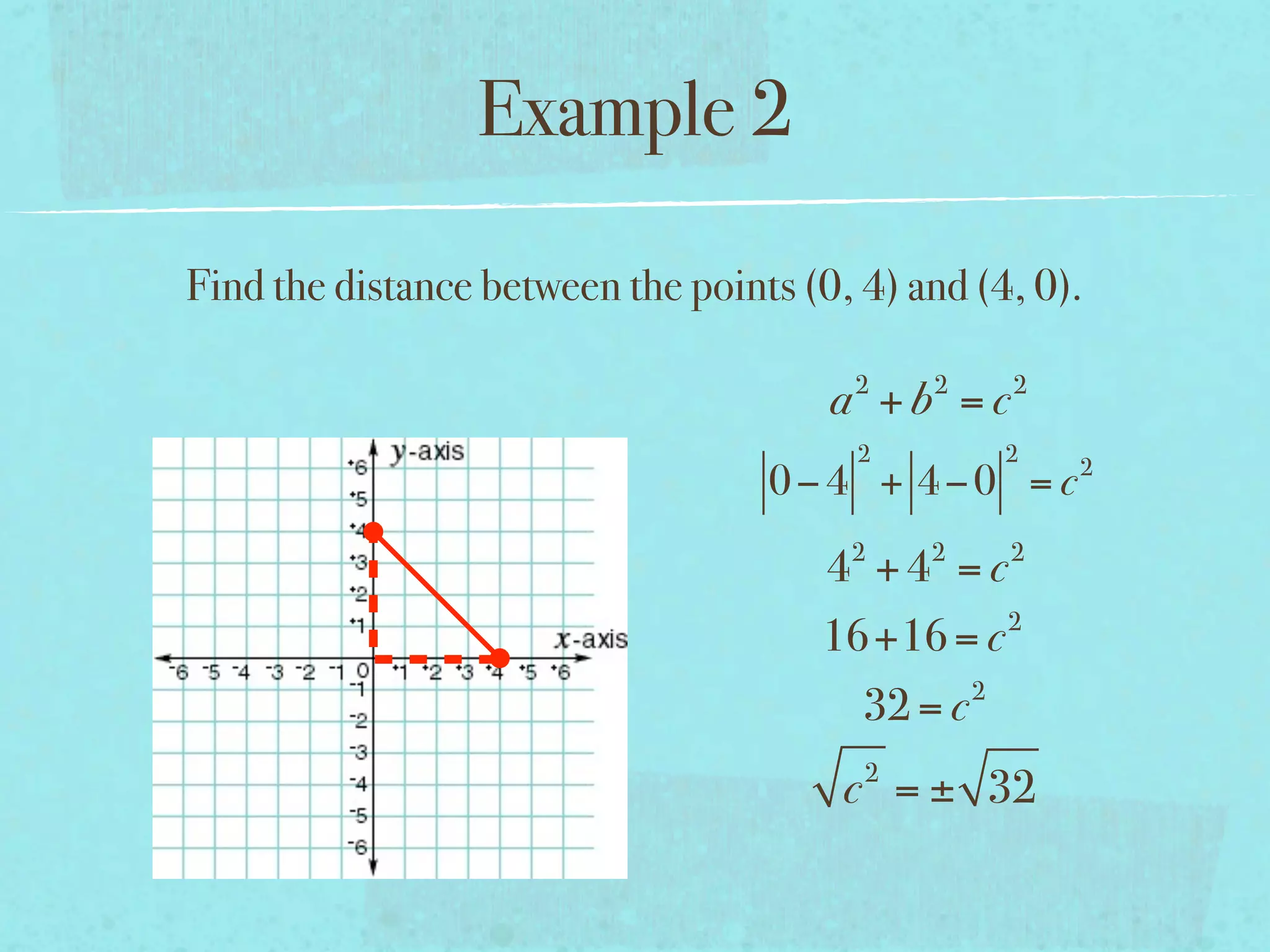
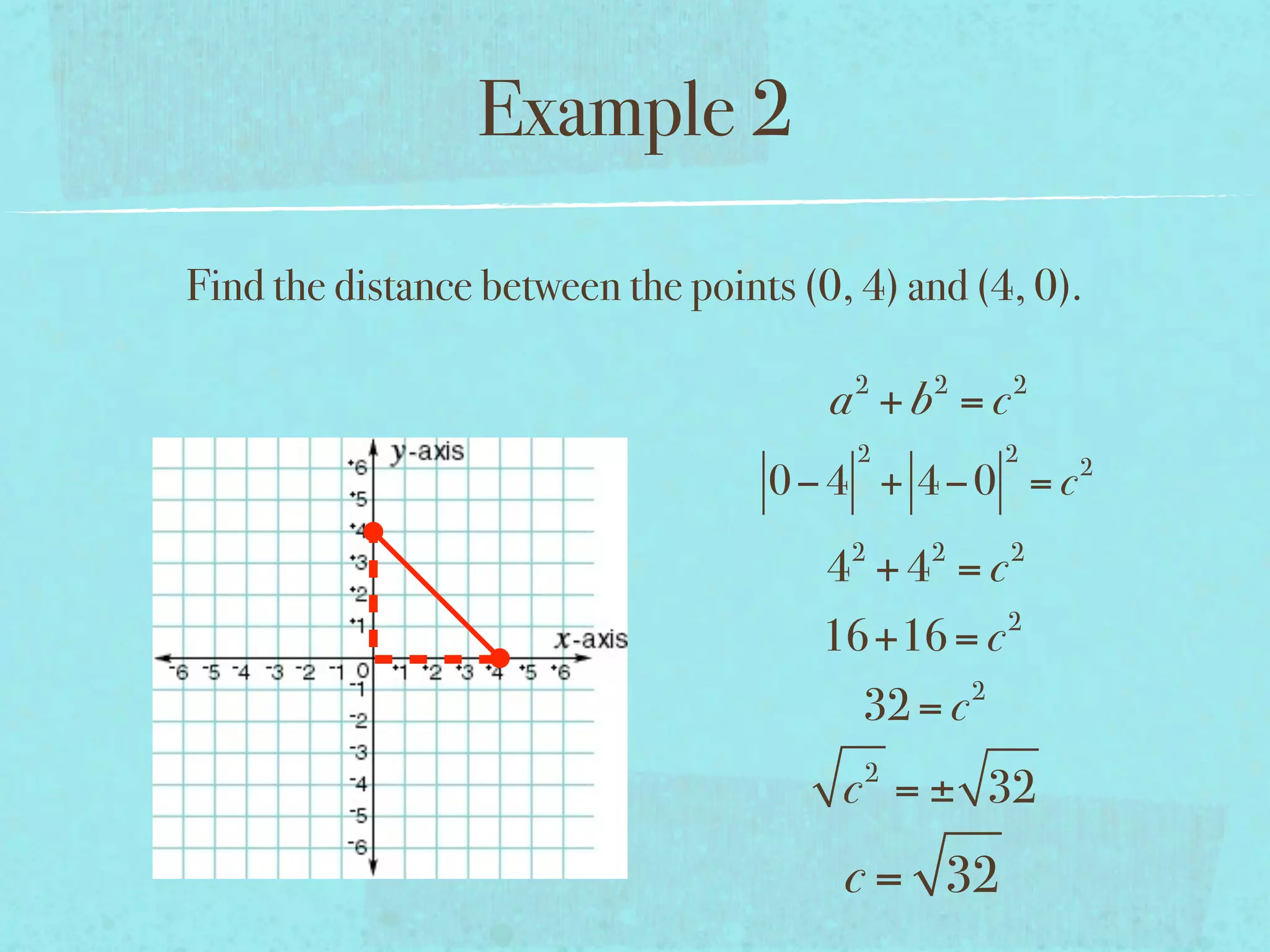
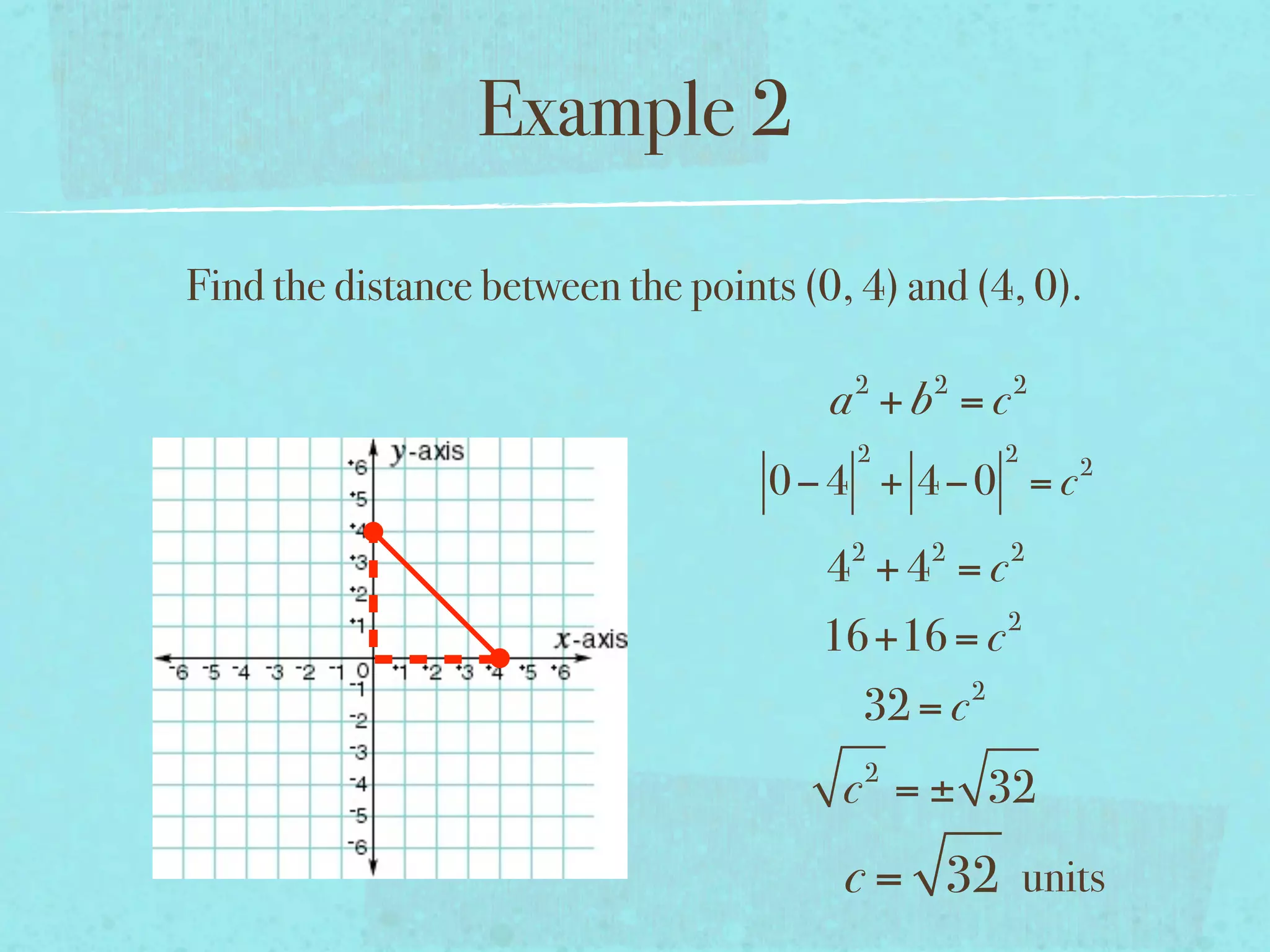
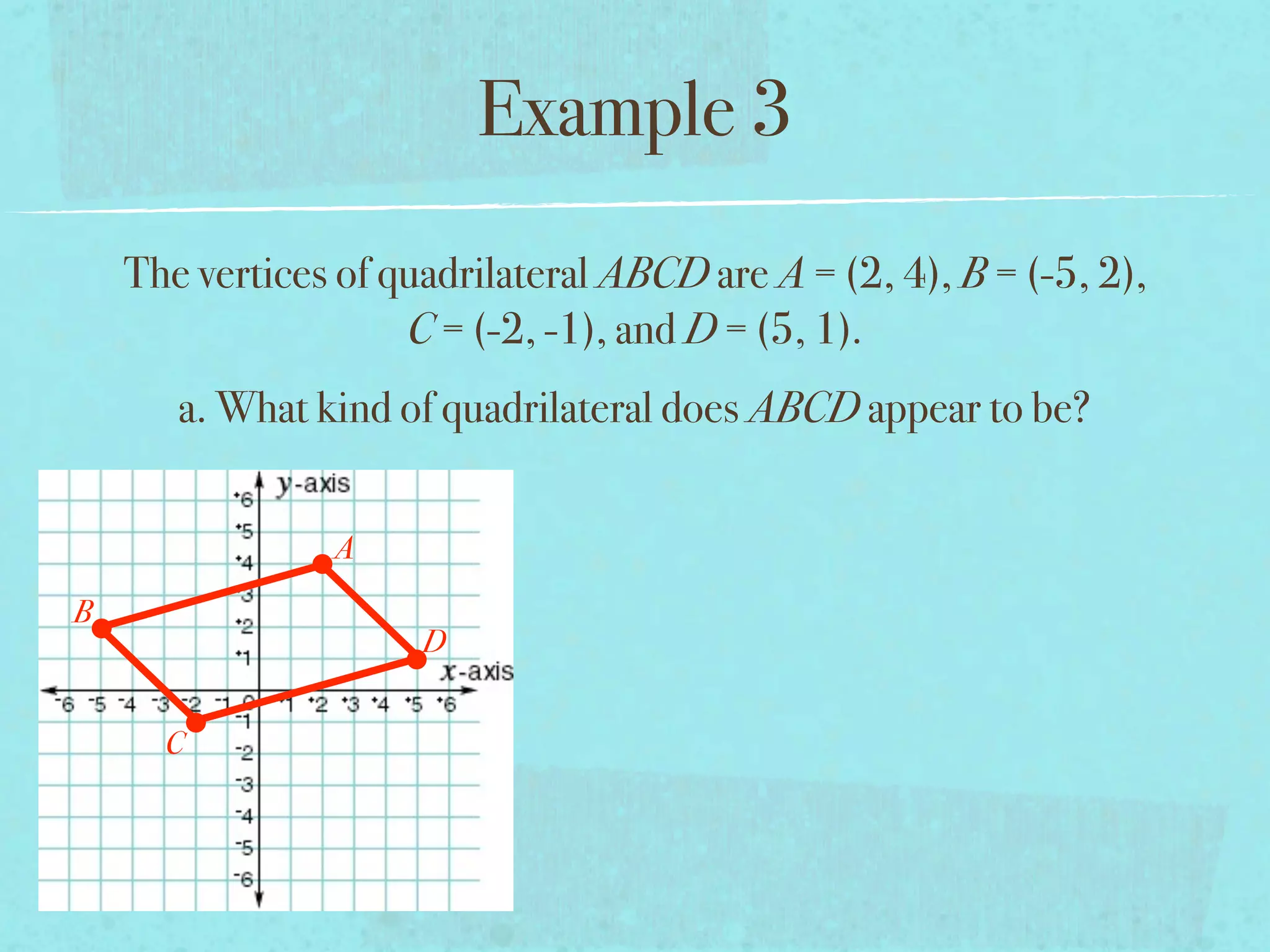
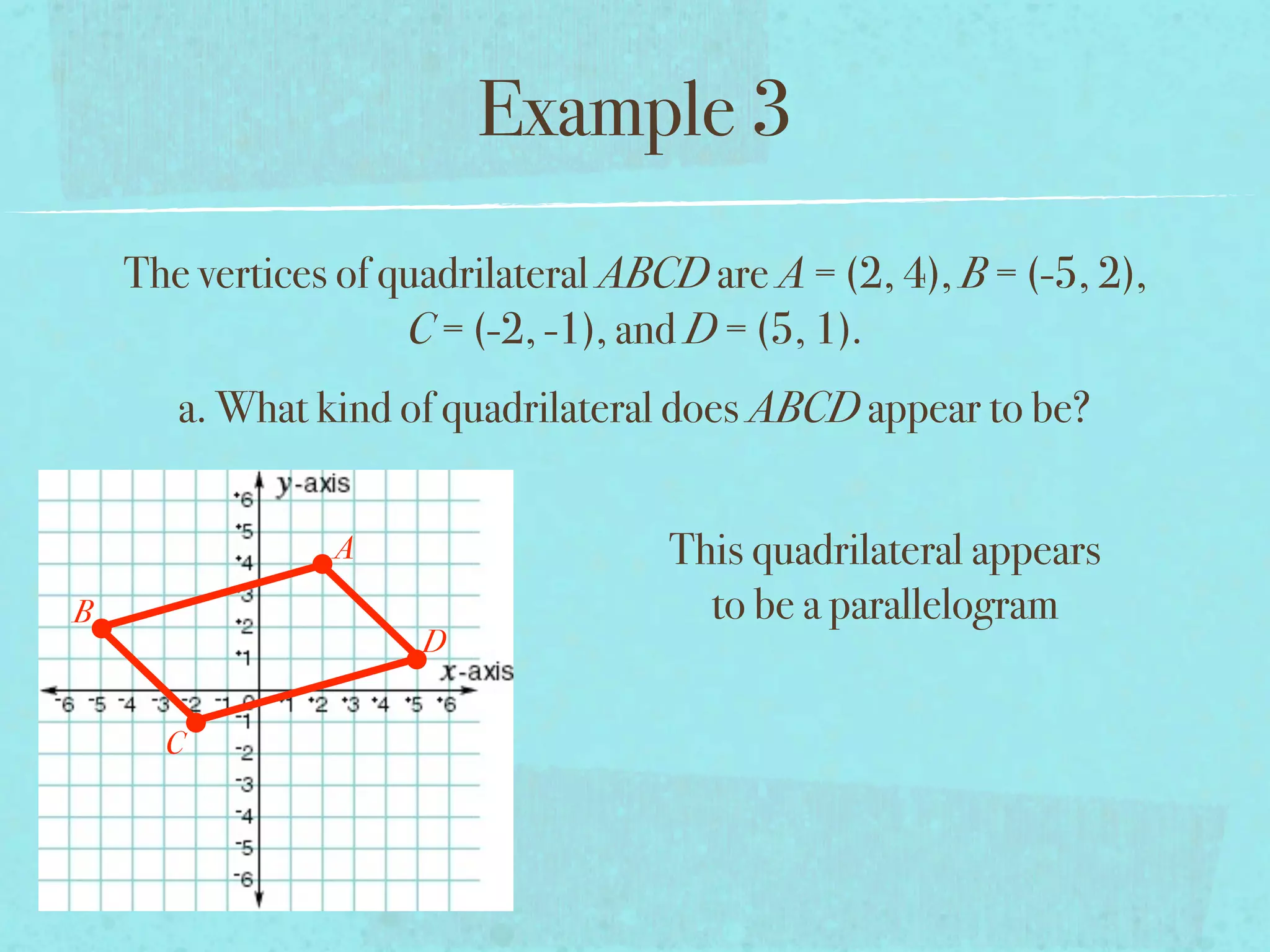
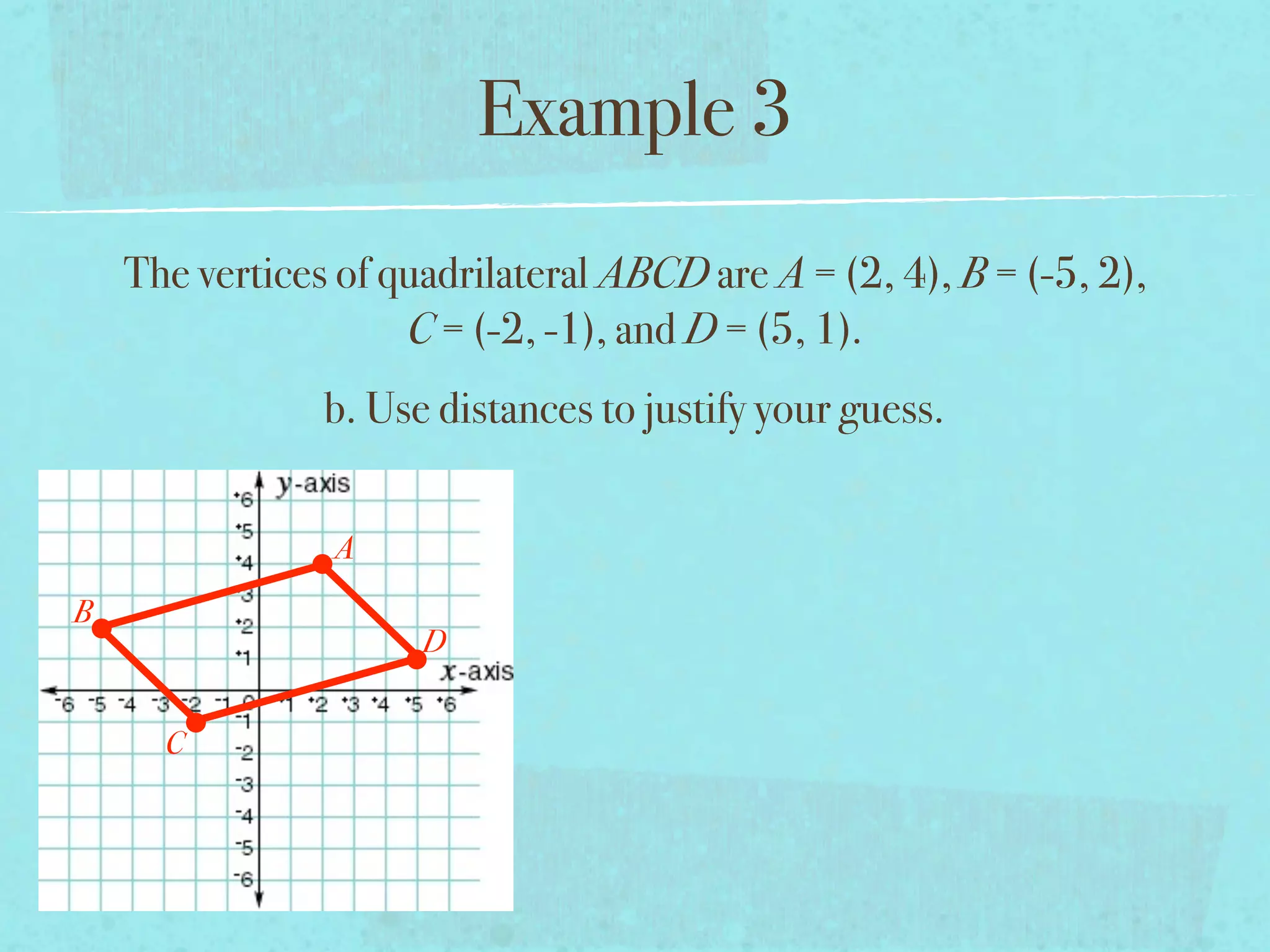
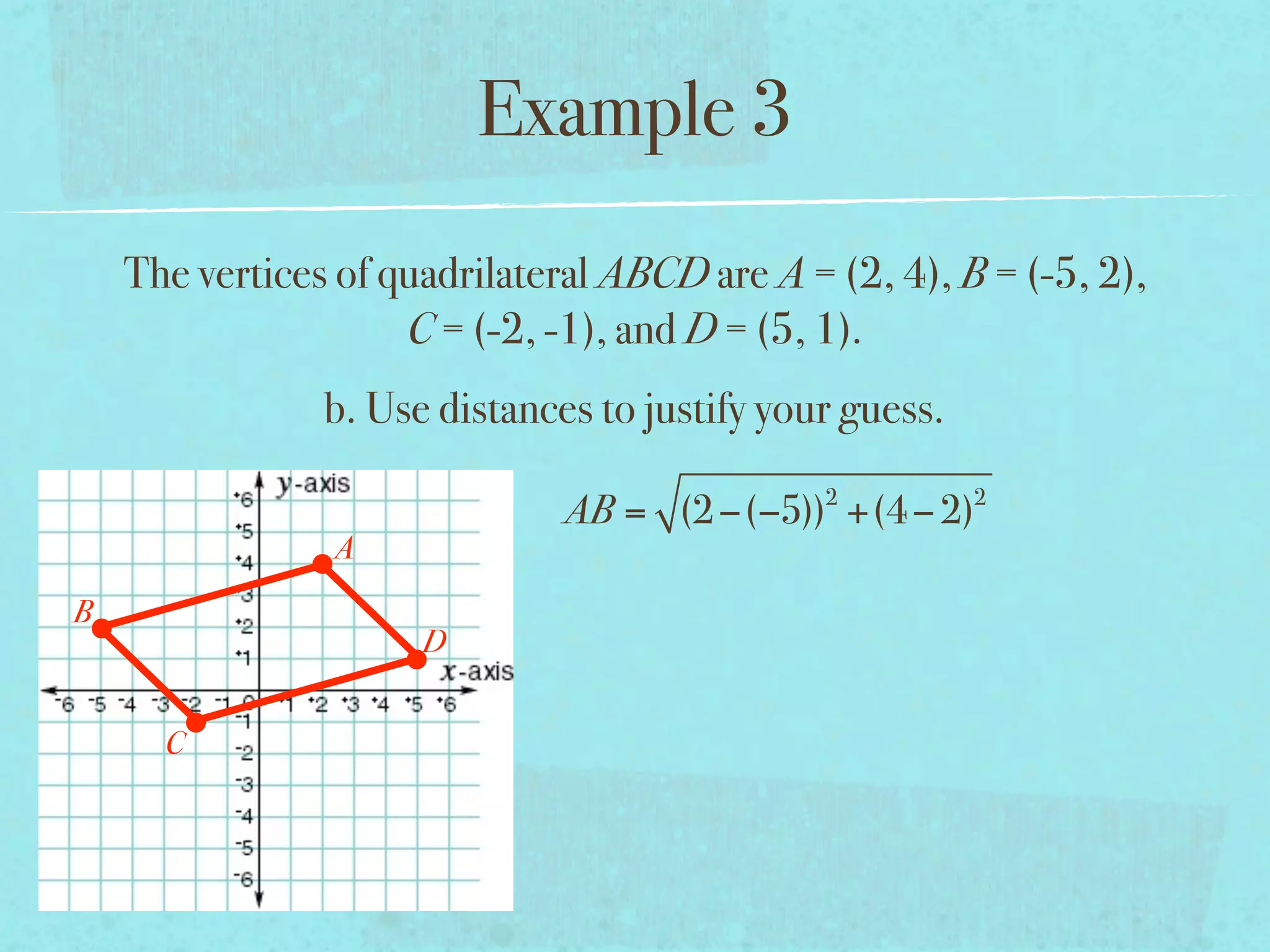
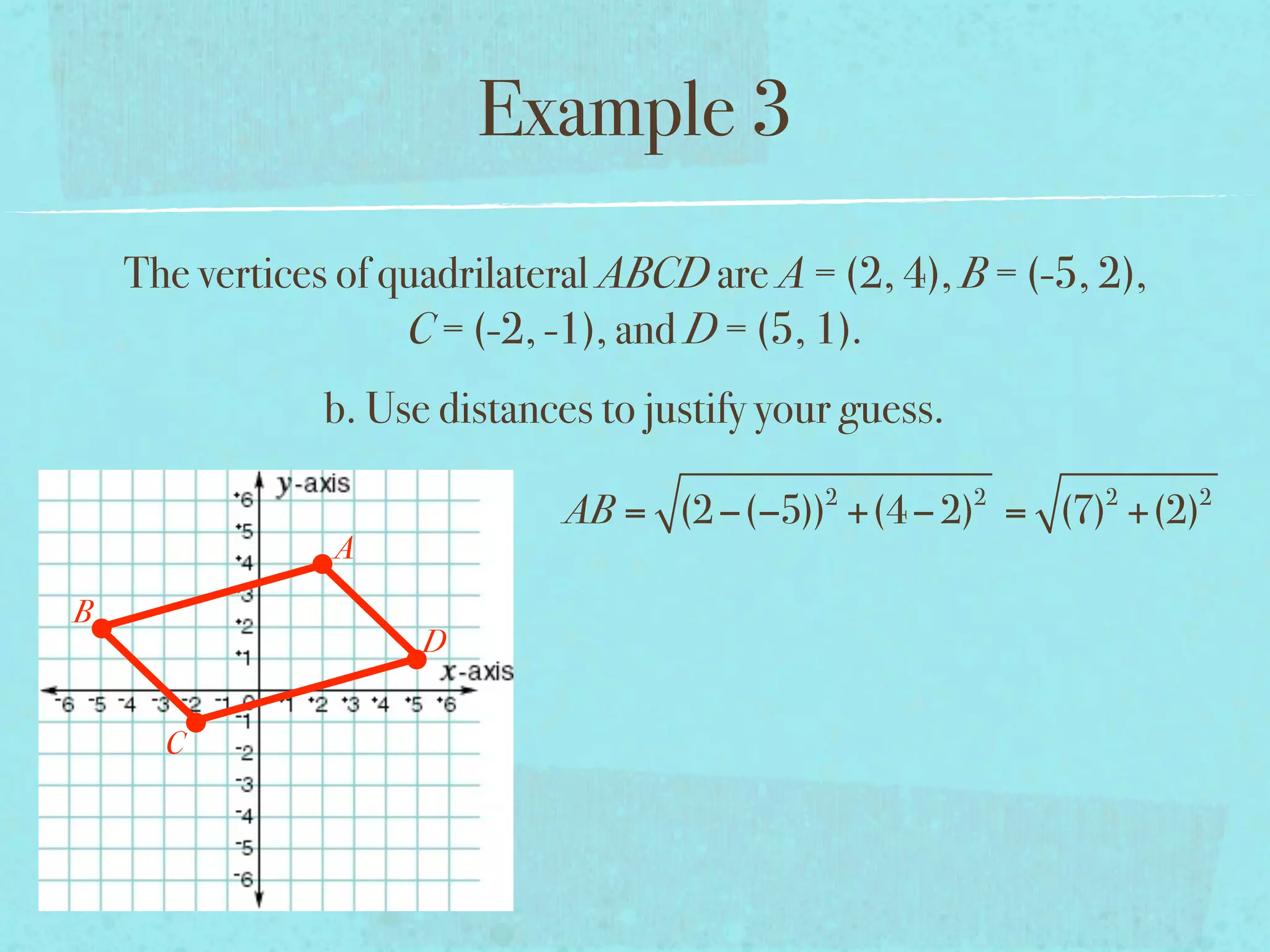
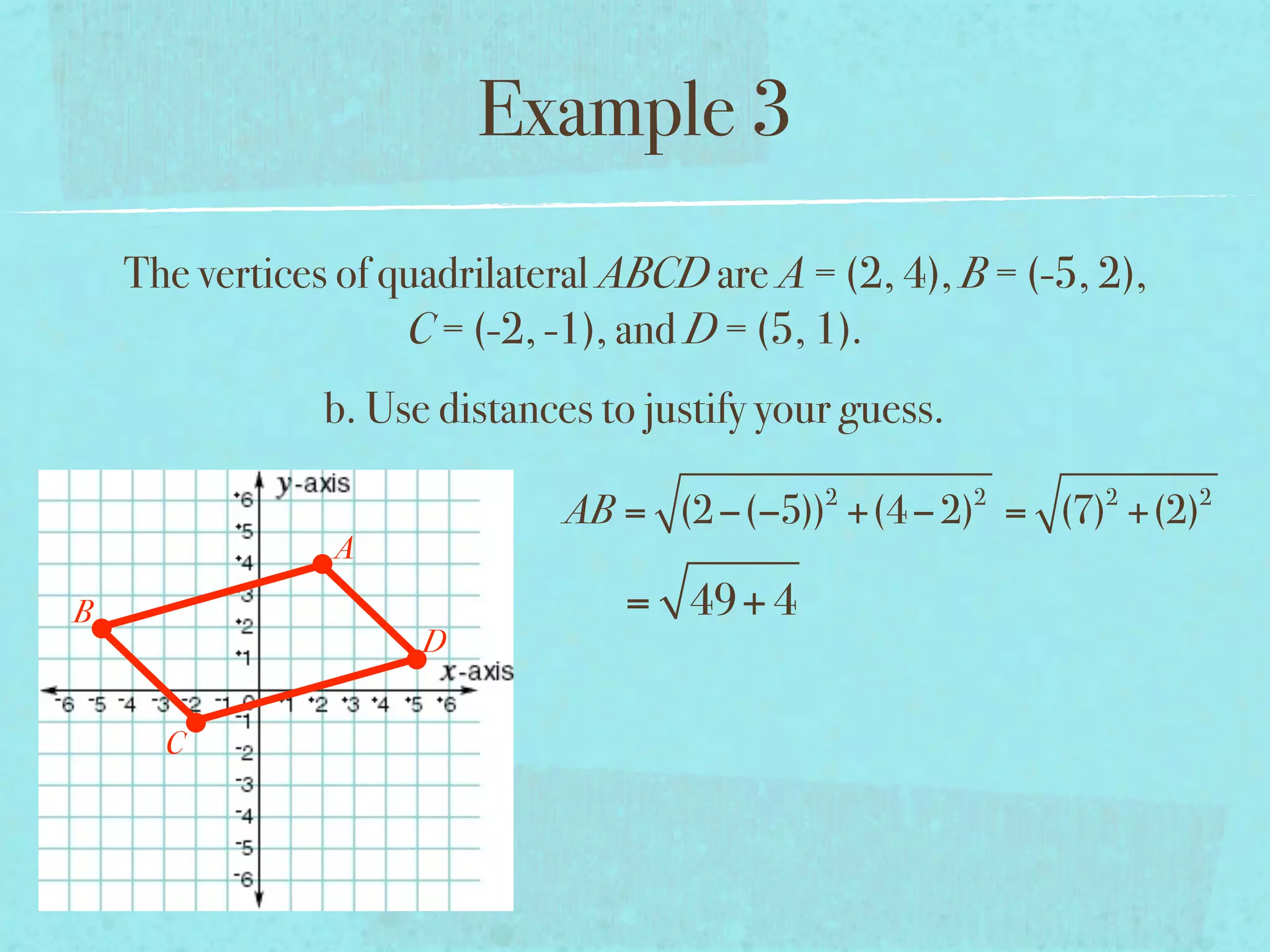
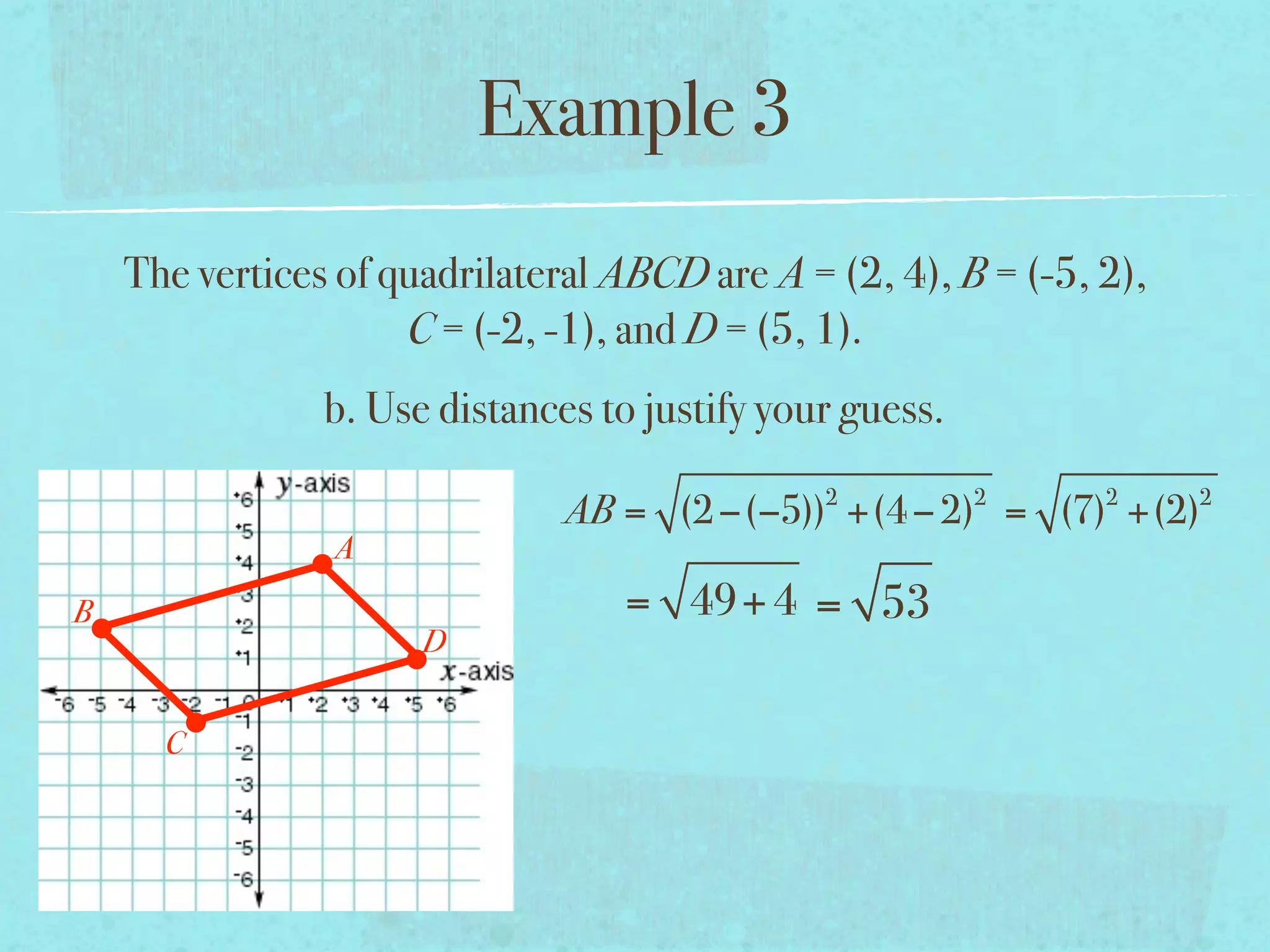
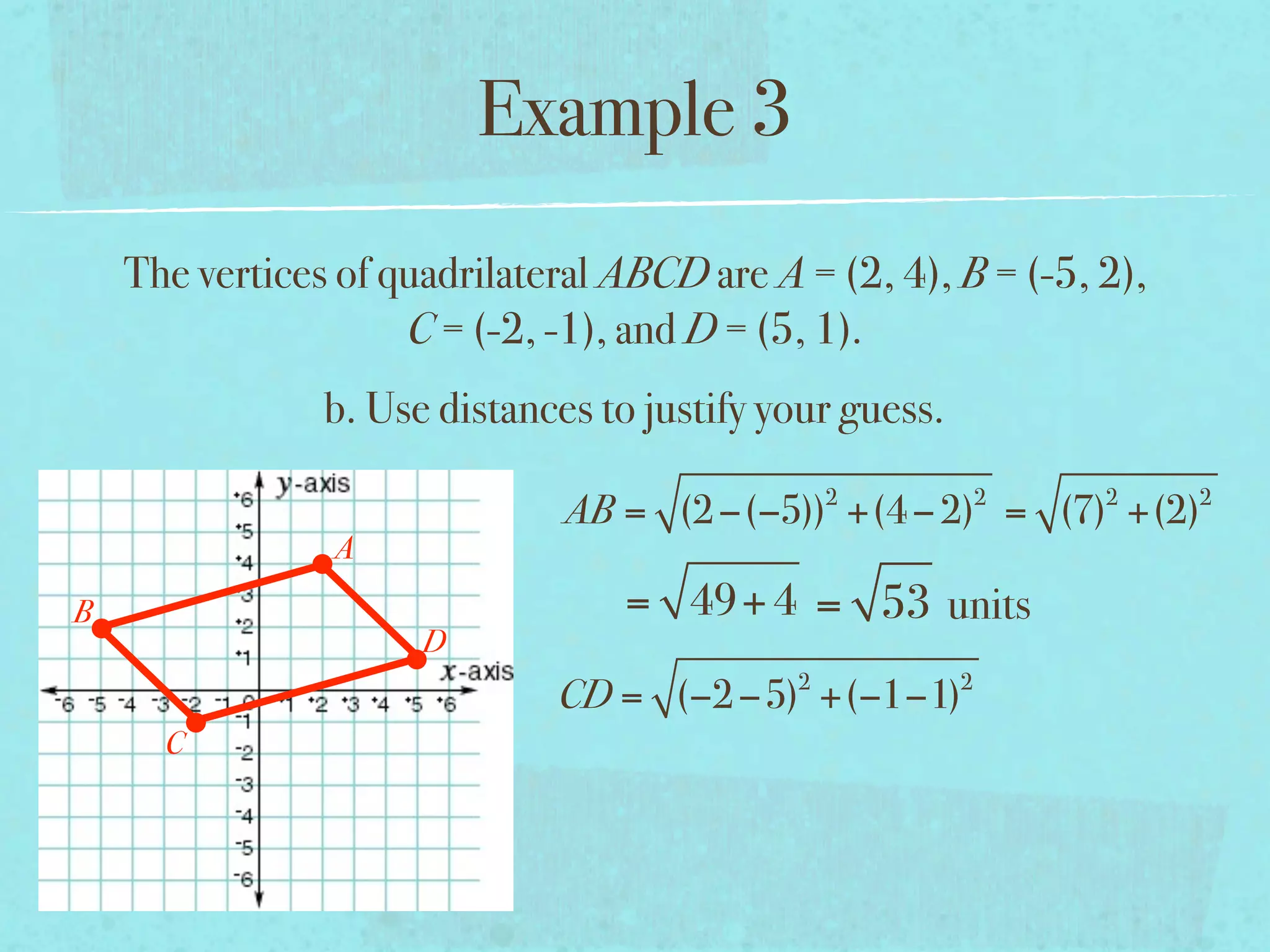
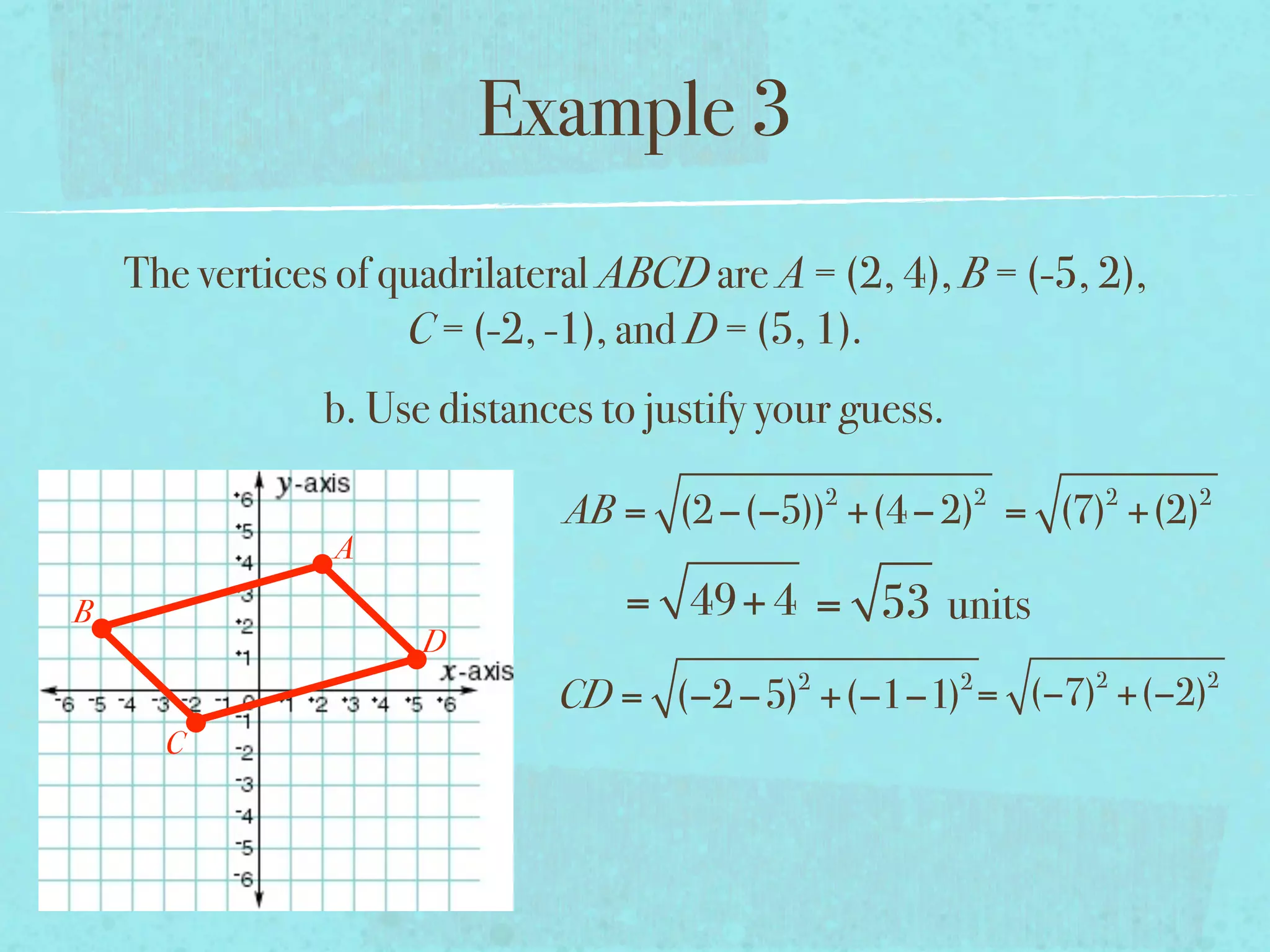
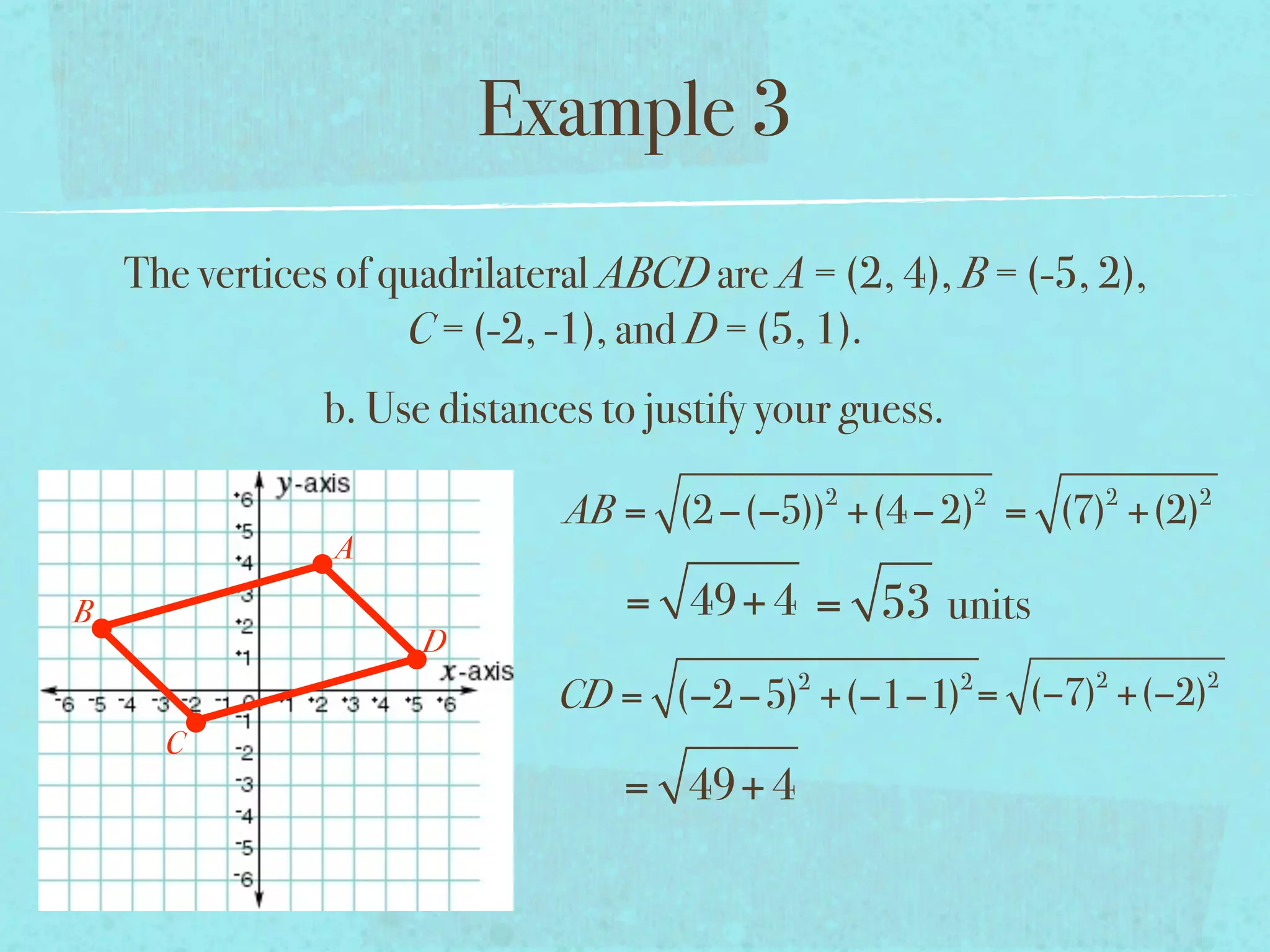
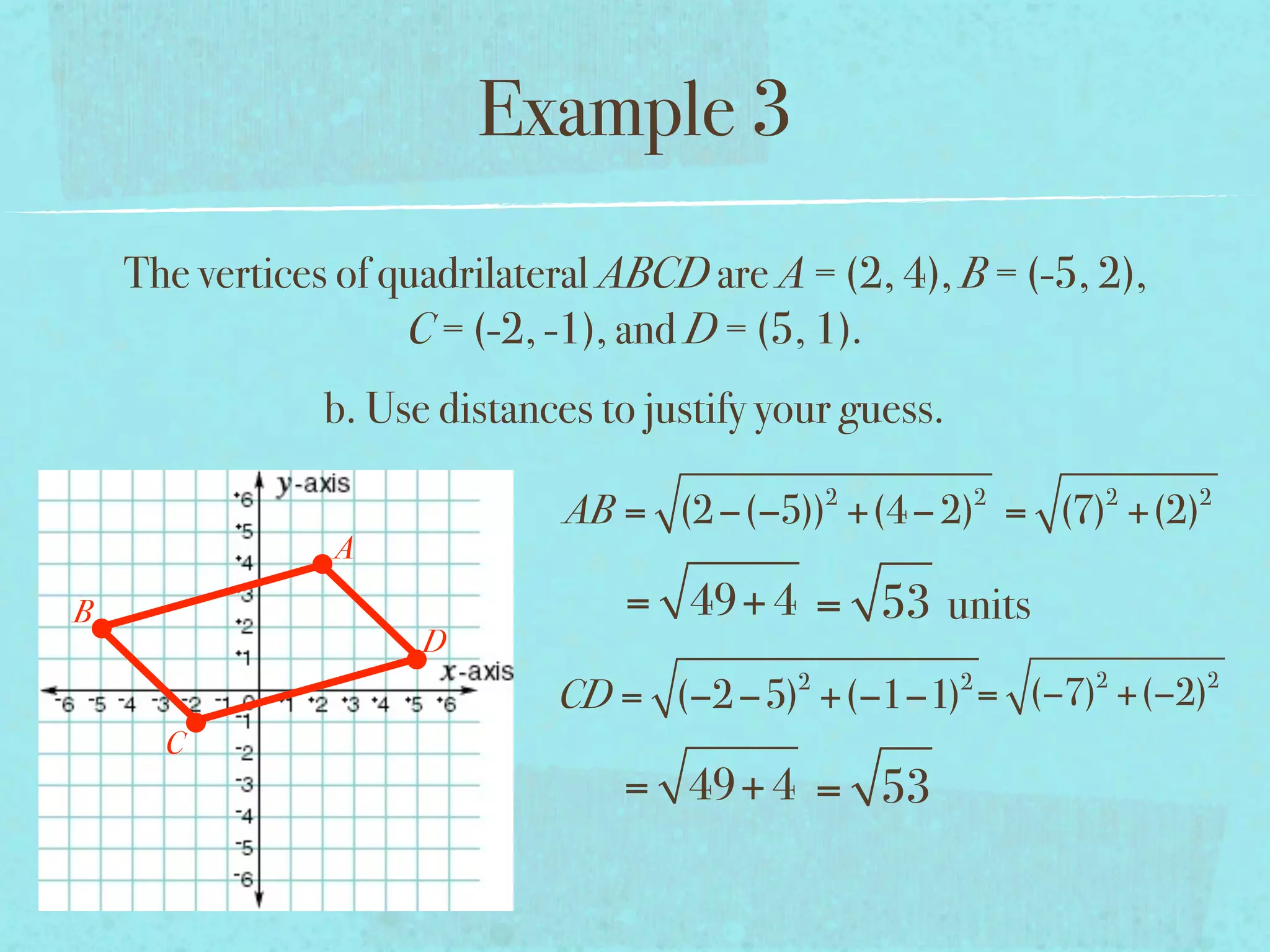
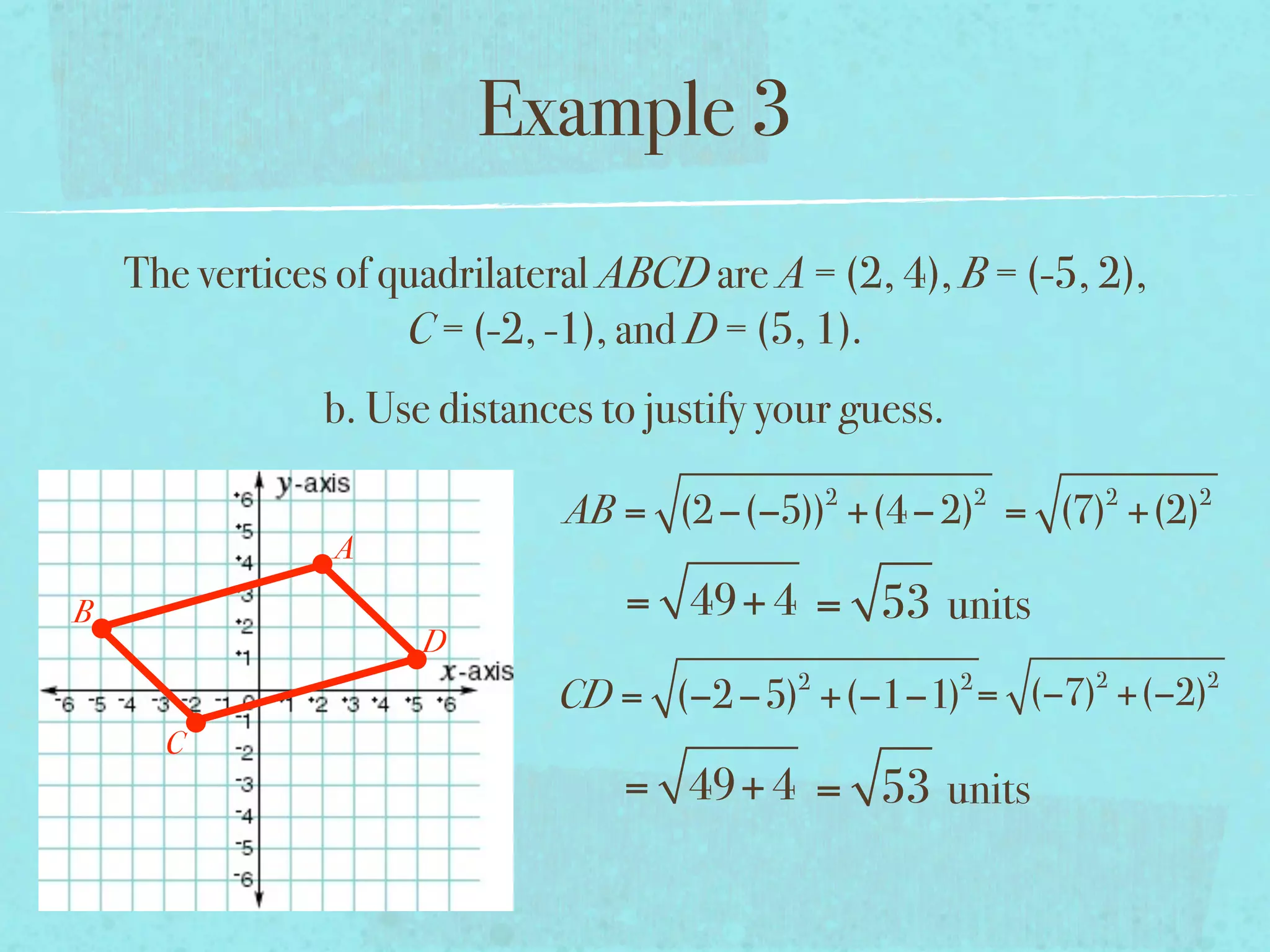
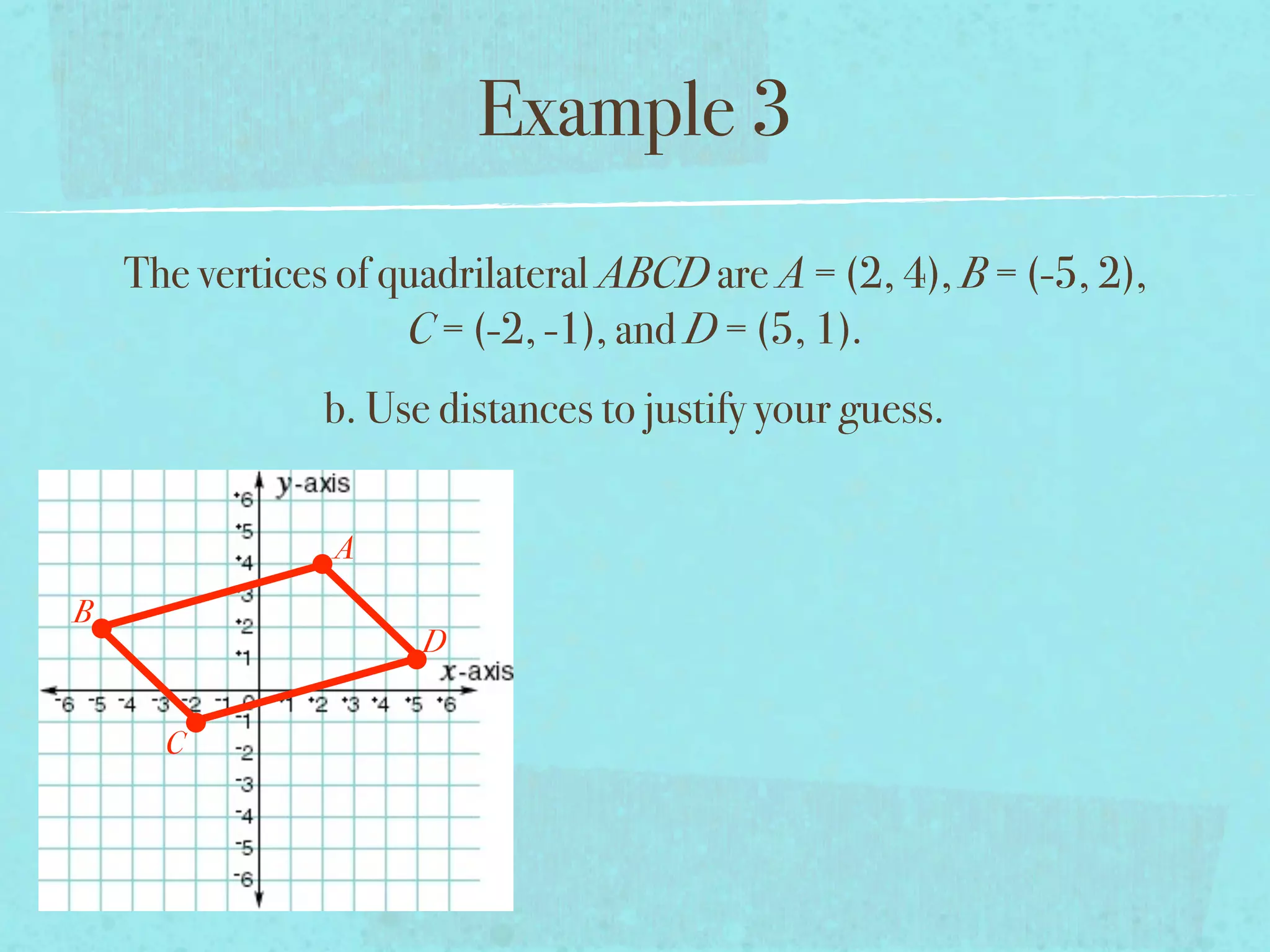
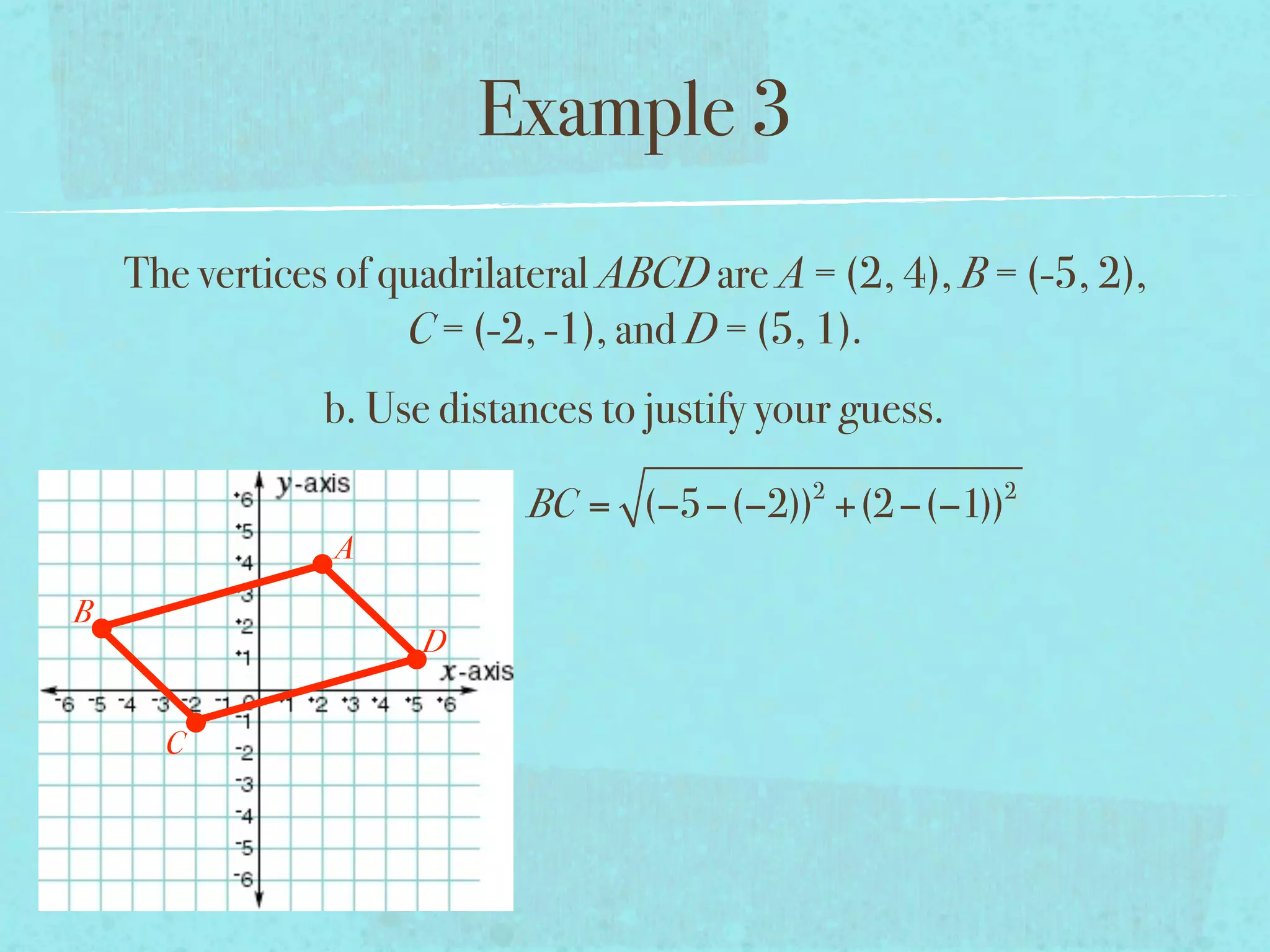
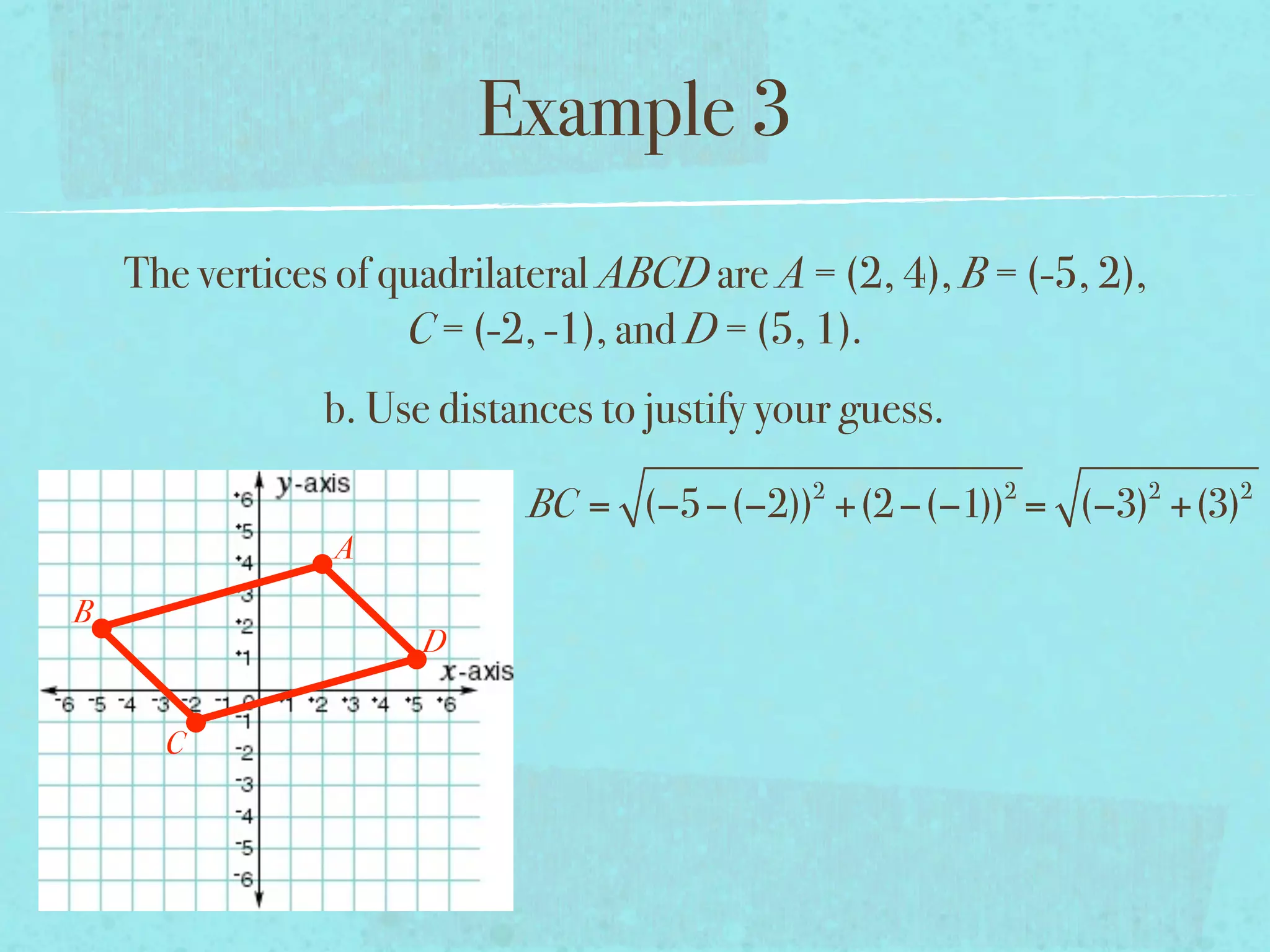
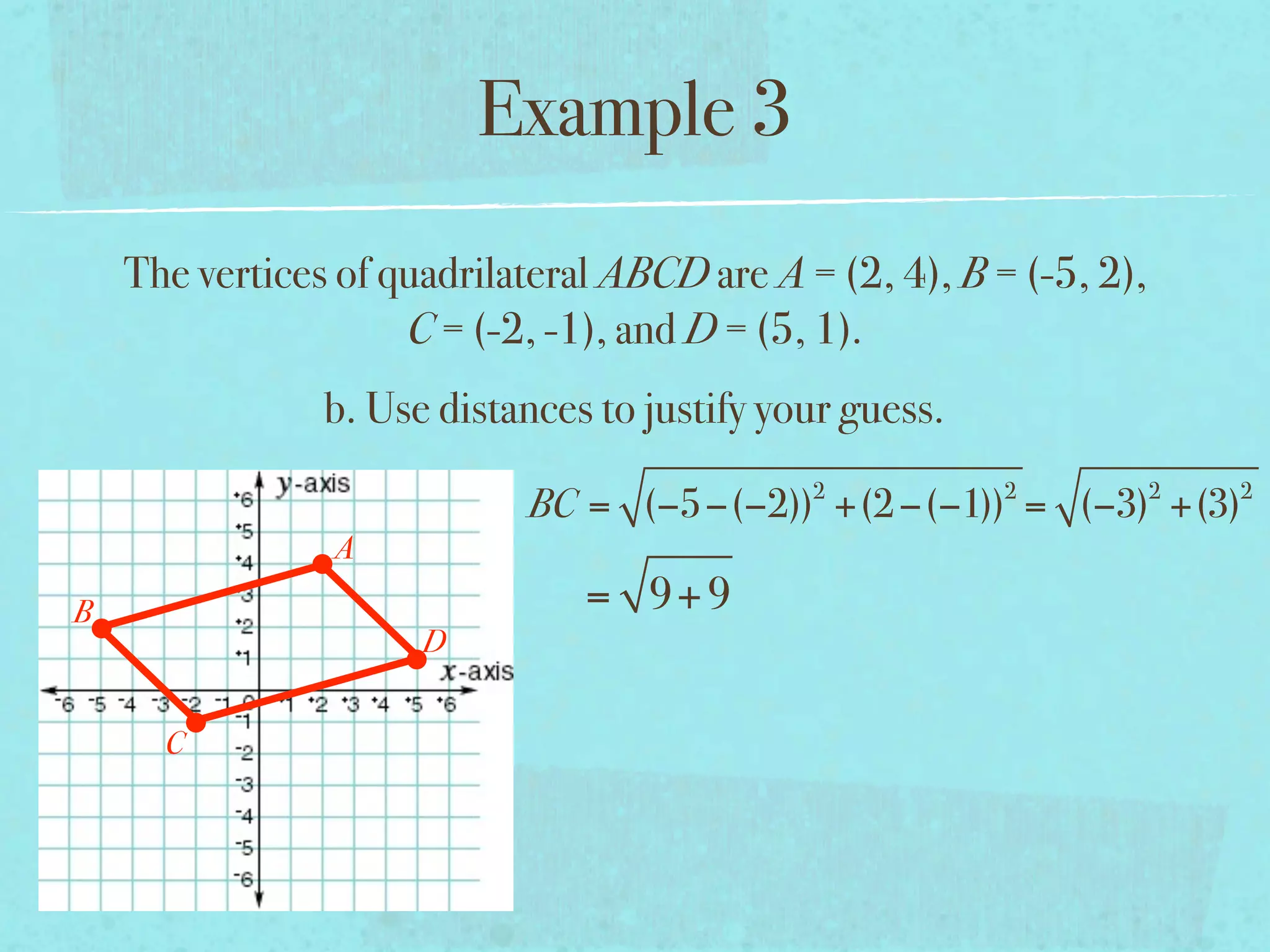
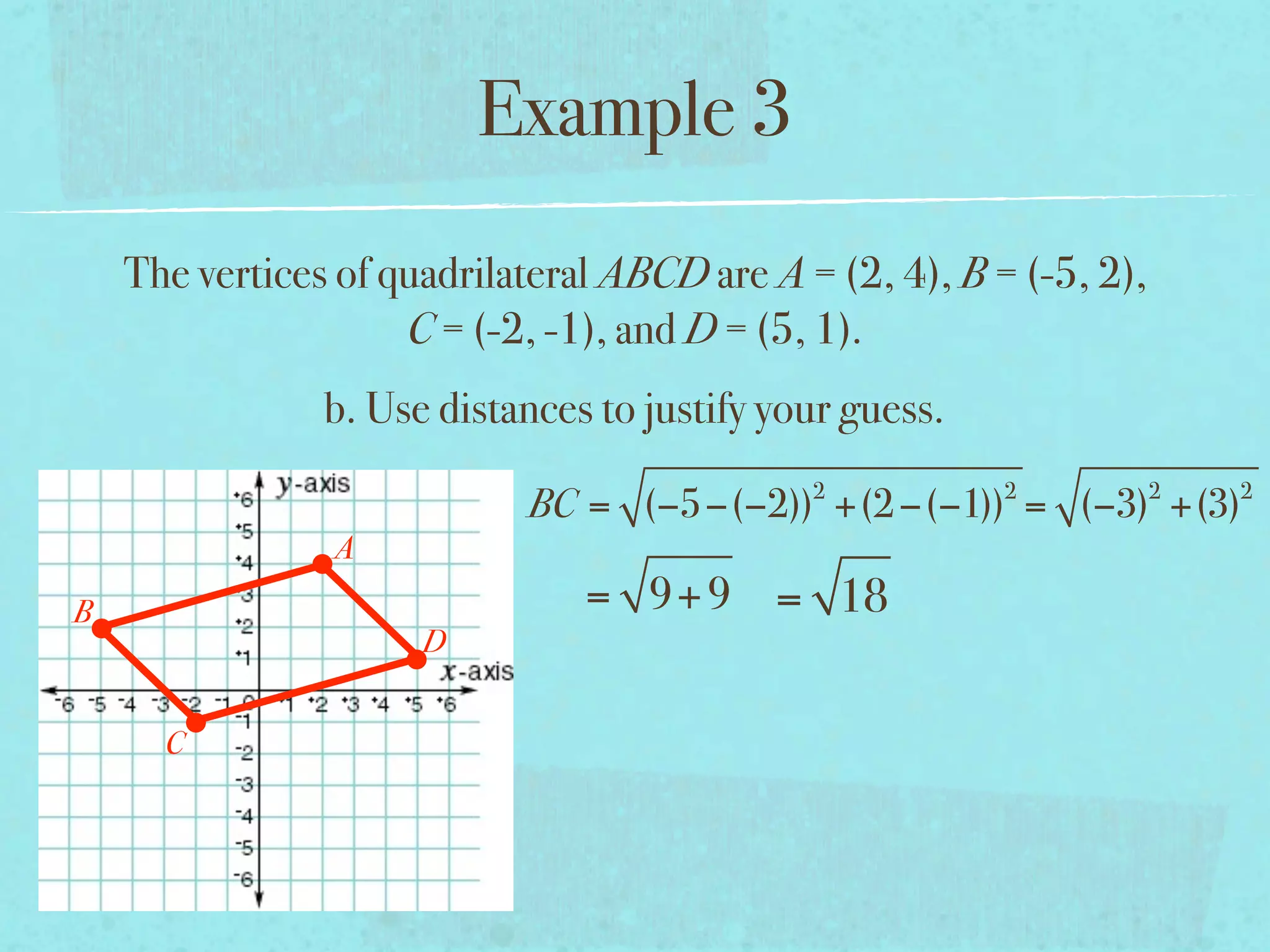
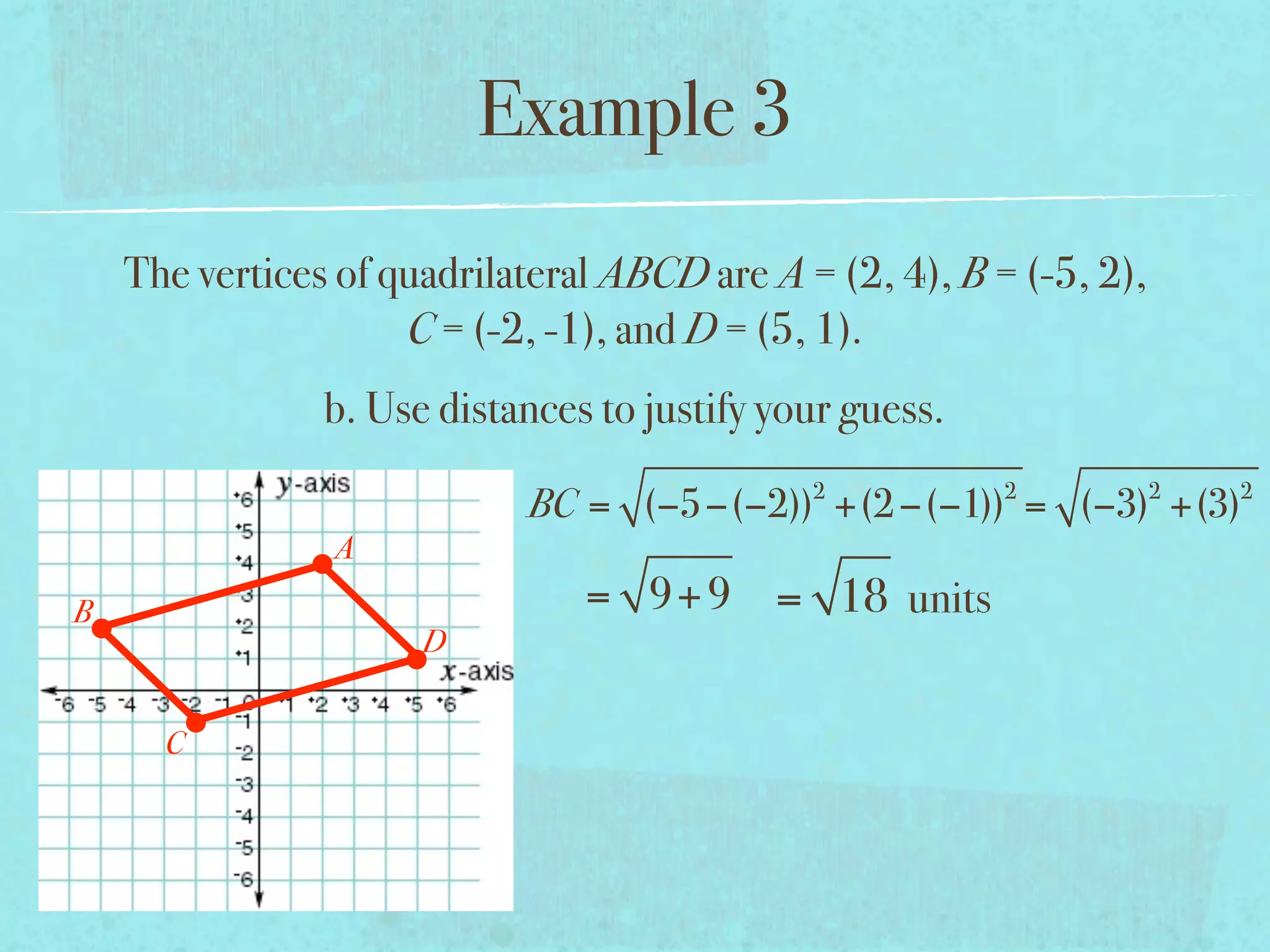
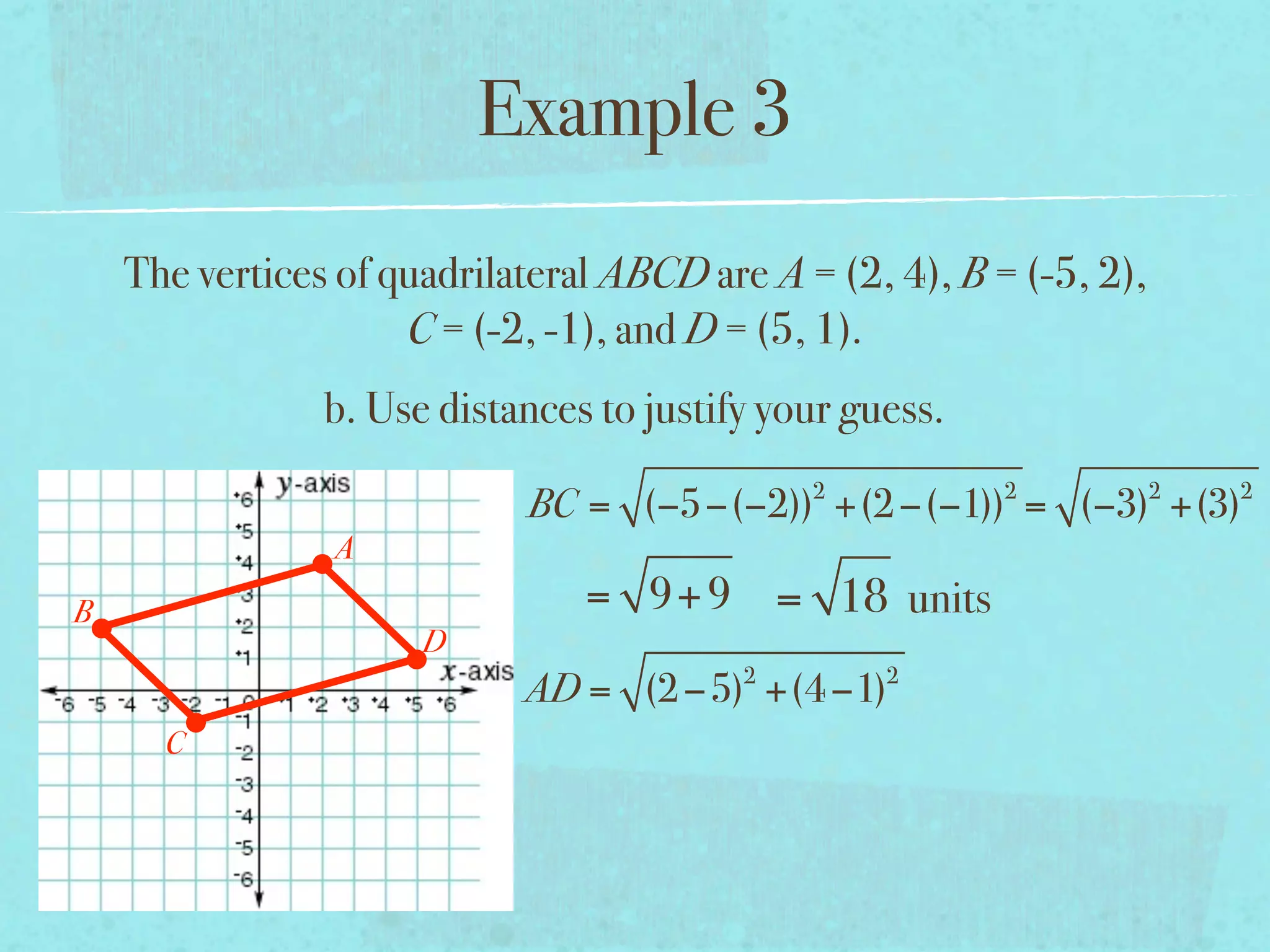
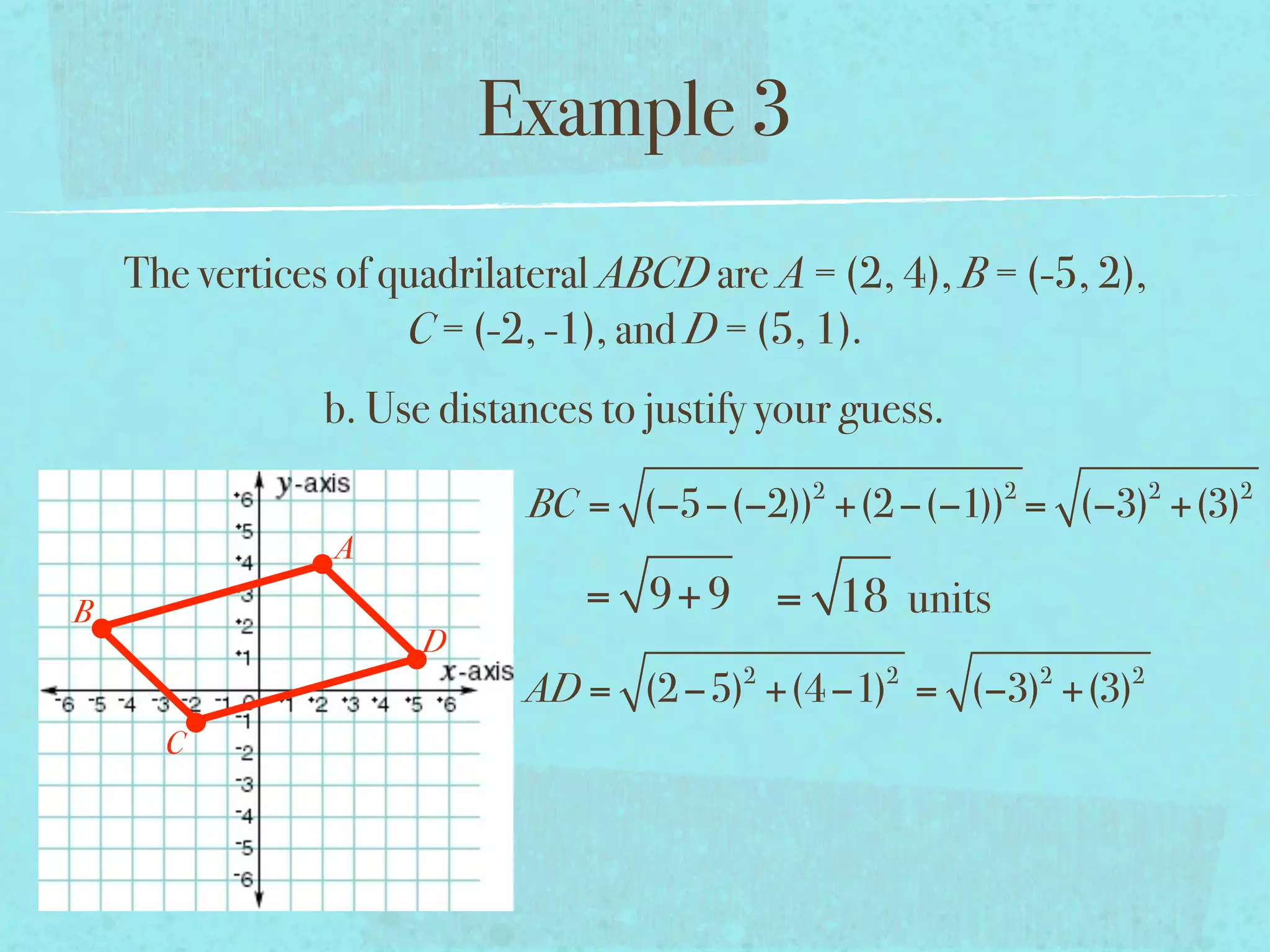
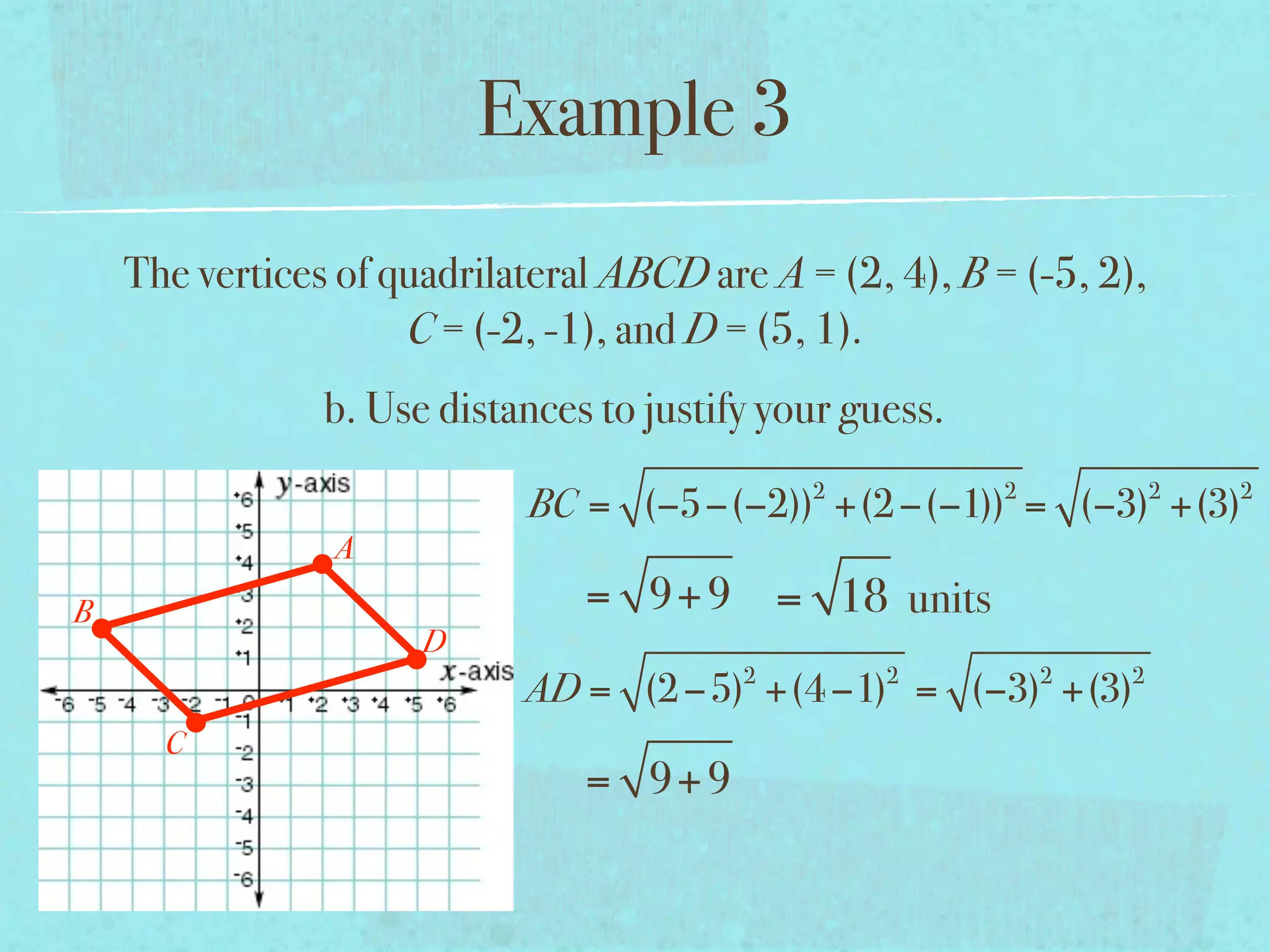
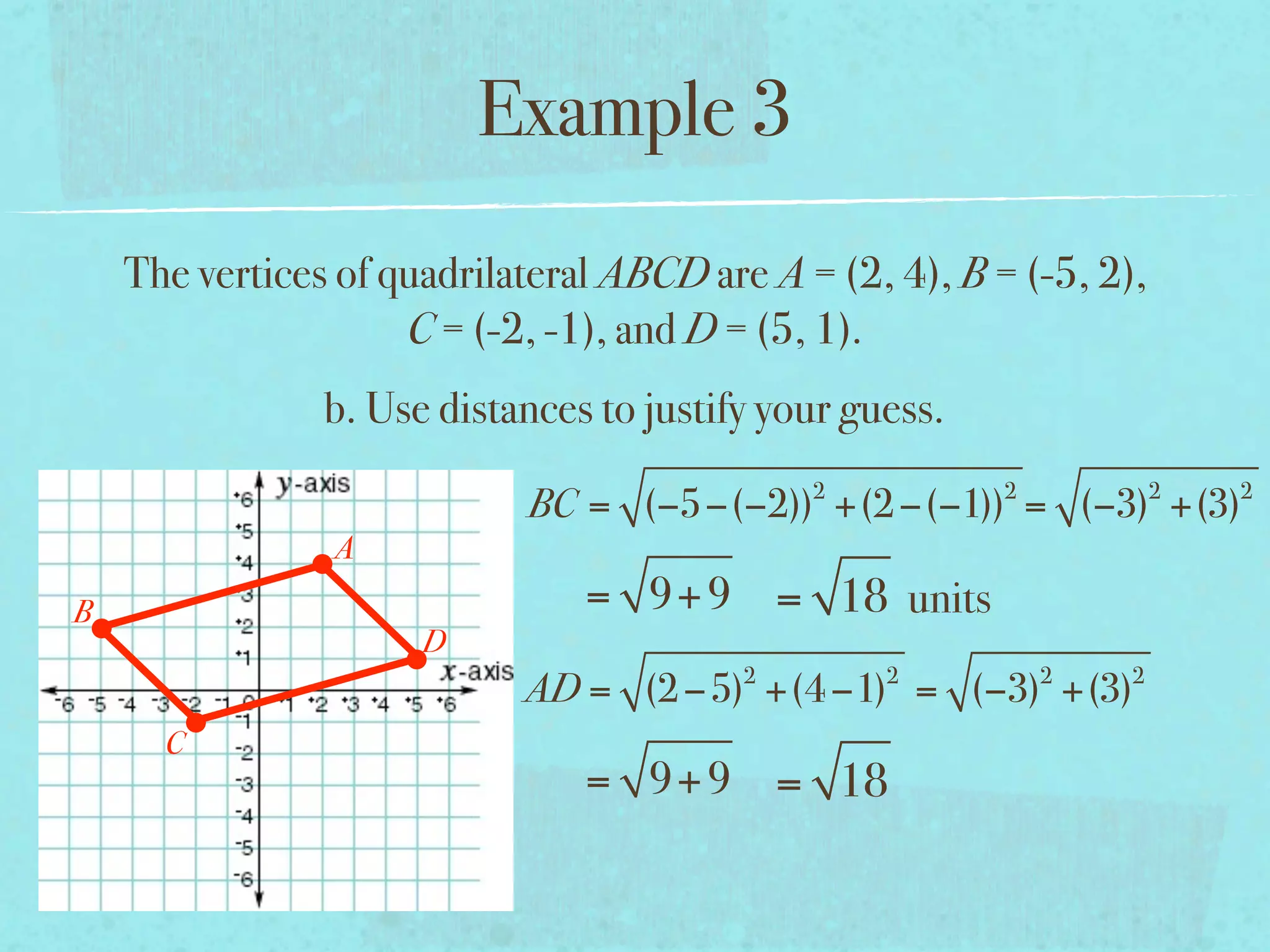
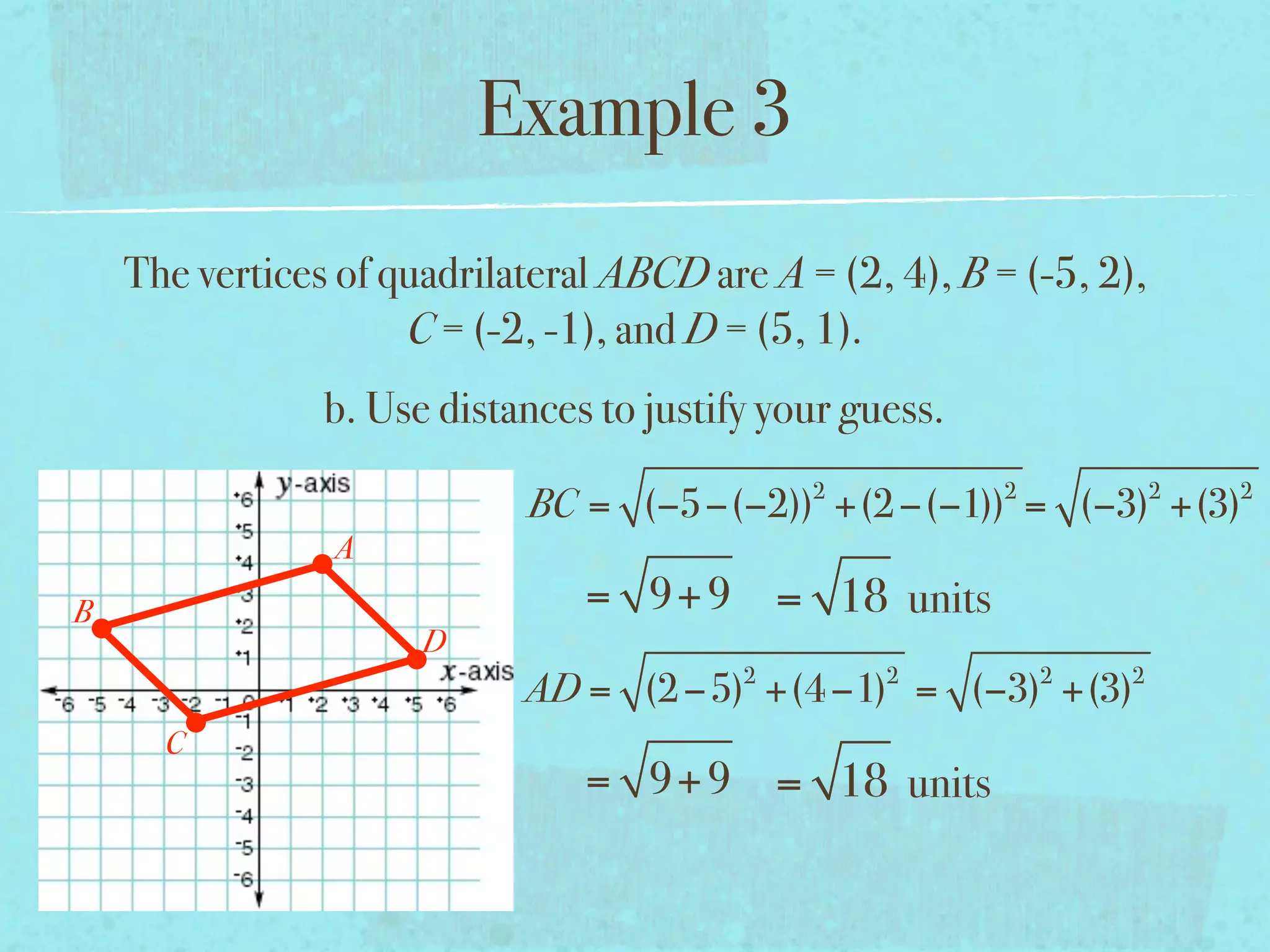
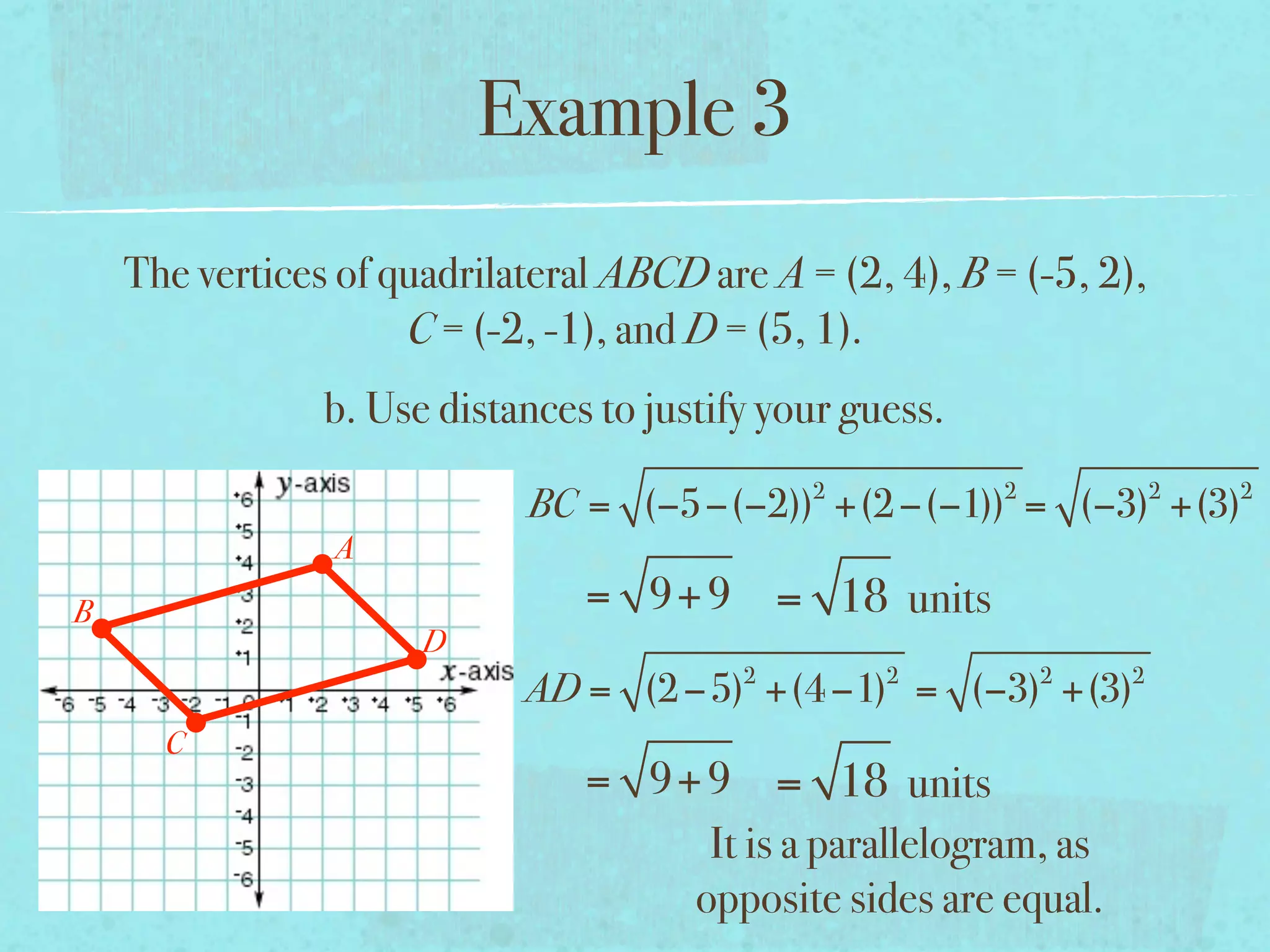
This document provides examples and explanations of key concepts related to graphing functions in the coordinate plane, including the distance and midpoint formulas. It begins by defining important vocabulary like coordinate plane, quadrants, axes and ordered pairs. It then works through two examples calculating the distance between points using the distance formula and finding the midpoint of a quadrilateral using the midpoint formula. The document explains that the distance formula is the Pythagorean theorem solved for the hypotenuse and the midpoint formula averages the x and y coordinates of two points.

1. Chapter 6
Graphing Functions

2. Section 6-1
Distance in the Coordinate Plane

3. Essential Questions
How do you use the distance formula to find the distance
between two points?
How do you use the midpoint formula?
Where you’ll see this:
Geography, market research, community service,
architecture

4. Vocabulary
1. Coordinate Plane:
2. Quadrants:
3. x-axis:
4. y-axis:
5. Ordered Pairs:
6. Origin:

5. Vocabulary
1. Coordinate Plane: Two number lines drawn perpendicular to each
other
2. Quadrants:
3. x-axis:
4. y-axis:
5. Ordered Pairs:
6. Origin:

6. Vocabulary
1. Coordinate Plane: Two number lines drawn perpendicular to each
other; used for graphing points
2. Quadrants:
3. x-axis:
4. y-axis:
5. Ordered Pairs:
6. Origin:

7. Vocabulary
1. Coordinate Plane: Two number lines drawn perpendicular to each
other; used for graphing points
2. Quadrants: Four areas created by the coordinate plane
3. x-axis:
4. y-axis:
5. Ordered Pairs:
6. Origin:

8. Vocabulary
1. Coordinate Plane: Two number lines drawn perpendicular to each
other; used for graphing points
2. Quadrants: Four areas created by the coordinate plane
3. x-axis: The horizontal axis on the coordinate plane
4. y-axis:
5. Ordered Pairs:
6. Origin:

9. Vocabulary
1. Coordinate Plane: Two number lines drawn perpendicular to each
other; used for graphing points
2. Quadrants: Four areas created by the coordinate plane
3. x-axis: The horizontal axis on the coordinate plane
4. y-axis: The vertical axis on the coordinate plane
5. Ordered Pairs:
6. Origin:

10. Vocabulary
1. Coordinate Plane: Two number lines drawn perpendicular to each
other; used for graphing points
2. Quadrants: Four areas created by the coordinate plane
3. x-axis: The horizontal axis on the coordinate plane
4. y-axis: The vertical axis on the coordinate plane
5. Ordered Pairs: Give us points in the form (x, y)
6. Origin:

11. Vocabulary
1. Coordinate Plane: Two number lines drawn perpendicular to each
other; used for graphing points
2. Quadrants: Four areas created by the coordinate plane
3. x-axis: The horizontal axis on the coordinate plane
4. y-axis: The vertical axis on the coordinate plane
5. Ordered Pairs: Give us points in the form (x, y)
6. Origin: The point (0, 0), which is where the x-axis and y-axis meet

12. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.

13. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
A

14. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
A B

15. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
C
A B

16. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
D C
A B

17. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
D C
A B

18. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
D C
AB = 4 −(−2)
A B

19. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
D C
AB = 4 −(−2) = 4 + 2
A B

20. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
D C
AB = 4 −(−2) = 4 + 2 = 6
A B

21. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
C
D AB = 4 −(−2) = 4 + 2 = 6 = 6
A B

22. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
C
D AB = 4 −(−2) = 4 + 2 = 6 = 6
AD = 5−(−2)
A B

23. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
C
D AB = 4 −(−2) = 4 + 2 = 6 = 6
AD = 5−(−2) = 5+ 2
A B

24. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
C
D AB = 4 −(−2) = 4 + 2 = 6 = 6
AD = 5−(−2) = 5+ 2 = 7
A B

25. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
C
D AB = 4 −(−2) = 4 + 2 = 6 = 6
AD = 5−(−2) = 5+ 2 = 7 = 7
A B

26. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
C
D AB = 4 −(−2) = 4 + 2 = 6 = 6
AD = 5−(−2) = 5+ 2 = 7 = 7
A B Area = lw

27. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
C
D AB = 4 −(−2) = 4 + 2 = 6 = 6
AD = 5−(−2) = 5+ 2 = 7 = 7
A B Area = lw = 6(7)

28. Example 1
The vertices of rectangle ABCD are as follows: A = (-2, -2),
B = (4, -2), C = (4, 5), and D = (-2, 5). Find the area of ABCD.
C
D AB = 4 −(−2) = 4 + 2 = 6 = 6
AD = 5−(−2) = 5+ 2 = 7 = 7
A B Area = lw = 6(7) = 42 square units

29. Example 2
Find the distance between the points (0, 4) and (4, 0).

30. Example 2
Find the distance between the points (0, 4) and (4, 0).

31. Example 2
Find the distance between the points (0, 4) and (4, 0).

32. Example 2
Find the distance between the points (0, 4) and (4, 0).

33. Example 2
Find the distance between the points (0, 4) and (4, 0).

34. Example 2
Find the distance between the points (0, 4) and (4, 0).
2 2 2
a +b =c

35. Example 2
Find the distance between the points (0, 4) and (4, 0).
2 2 2
a +b =c
2 2
2
0−4 + 4−0 = c

36. Example 2
Find the distance between the points (0, 4) and (4, 0).
2 2 2
a +b =c
2 2
2
0−4 + 4−0 = c
2 2 2
4 +4 = c

37. Example 2
Find the distance between the points (0, 4) and (4, 0).
2 2 2
a +b =c
2 2
2
0−4 + 4−0 = c
2 2 2
4 +4 = c
2
16+16 = c

38. Example 2
Find the distance between the points (0, 4) and (4, 0).
2 2 2
a +b =c
2 2
2
0−4 + 4−0 = c
2 2 2
4 +4 = c
2
16+16 = c
2
32 = c

39. Example 2
Find the distance between the points (0, 4) and (4, 0).
2 2 2
a +b =c
2 2
2
0−4 + 4−0 = c
2 2 2
4 +4 = c
2
16+16 = c
2
32 = c
2
c = ± 32

40. Example 2
Find the distance between the points (0, 4) and (4, 0).
2 2 2
a +b =c
2 2
2
0−4 + 4−0 = c
2 2 2
4 +4 = c
2
16+16 = c
2
32 = c
2
c = ± 32
c = 32

41. Example 2
Find the distance between the points (0, 4) and (4, 0).
2 2 2
a +b =c
2 2
2
0−4 + 4−0 = c
2 2 2
4 +4 = c
2
16+16 = c
2
32 = c
2
c = ± 32
c = 32 units

42. Distance Formula:
Midpoint Formula:

43. Distance Formula: d = (x1 − x2 )2 +( y1 − y2 )2 , for points (x1 , y1 ),(x2 , y2 )
Midpoint Formula:

44. Distance Formula: d = (x1 − x2 )2 +( y1 − y2 )2 , for points (x1 , y1 ),(x2 , y2 )
This is nothing more than the Pythagorean Formula solved for c.
Midpoint Formula:

45. Distance Formula: d = (x1 − x2 )2 +( y1 − y2 )2 , for points (x1 , y1 ),(x2 , y2 )
This is nothing more than the Pythagorean Formula solved for c.
 x1 + x2 y1 + y2 
Midpoint Formula: M =  ,  , for points (x1 , y1 ),(x2 , y2 )
 2 2 

46. Distance Formula: d = (x1 − x2 )2 +( y1 − y2 )2 , for points (x1 , y1 ),(x2 , y2 )
This is nothing more than the Pythagorean Formula solved for c.
 x1 + x2 y1 + y2 
Midpoint Formula: M =  ,  , for points (x1 , y1 ),(x2 , y2 )
 2 2 
This is nothing more than averaging the x and y coordinates.

47. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
a. What kind of quadrilateral does ABCD appear to be?

48. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
a. What kind of quadrilateral does ABCD appear to be?
A

49. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
a. What kind of quadrilateral does ABCD appear to be?
A
B

50. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
a. What kind of quadrilateral does ABCD appear to be?
A
B
C

51. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
a. What kind of quadrilateral does ABCD appear to be?
A
B
D
C

52. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
a. What kind of quadrilateral does ABCD appear to be?
A
B
D
C

53. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
a. What kind of quadrilateral does ABCD appear to be?
A This quadrilateral appears
B to be a parallelogram
D
C

54. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
A
B
D
C

55. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2
AB = (2 −(−5)) +(4 − 2)
A
B
D
C

56. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
AB = (2 −(−5)) +(4 − 2) = (7) +(2)
A
B
D
C

57. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
AB = (2 −(−5)) +(4 − 2) = (7) +(2)
A
B = 49+ 4
D
C

58. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
AB = (2 −(−5)) +(4 − 2) = (7) +(2)
A
B = 49+ 4 = 53
D
C

59. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
AB = (2 −(−5)) +(4 − 2) = (7) +(2)
A
B = 49+ 4 = 53 units
D
C

60. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
AB = (2 −(−5)) +(4 − 2) = (7) +(2)
A
B = 49+ 4 = 53 units
D
CD = (−2 −5)2 +(−1−1)2
C

61. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
AB = (2 −(−5)) +(4 − 2) = (7) +(2)
A
B = 49+ 4 = 53 units
D
2 2 2 2
CD = (−2 −5) +(−1−1) = (−7) +(−2)
C

62. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
AB = (2 −(−5)) +(4 − 2) = (7) +(2)
A
B = 49+ 4 = 53 units
D
2 2 2 2
CD = (−2 −5) +(−1−1) = (−7) +(−2)
C
= 49+ 4

63. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
AB = (2 −(−5)) +(4 − 2) = (7) +(2)
A
B = 49+ 4 = 53 units
D
2 2 2 2
CD = (−2 −5) +(−1−1) = (−7) +(−2)
C
= 49+ 4 = 53

64. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
AB = (2 −(−5)) +(4 − 2) = (7) +(2)
A
B = 49+ 4 = 53 units
D
2 2 2 2
CD = (−2 −5) +(−1−1) = (−7) +(−2)
C
= 49+ 4 = 53 units

65. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
A
B
D
C

66. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2
BC = (−5−(−2)) +(2 −(−1))
A
B
D
C

67. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
BC = (−5−(−2)) +(2 −(−1)) = (−3) +(3)
A
B
D
C

68. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
BC = (−5−(−2)) +(2 −(−1)) = (−3) +(3)
A
B = 9+ 9
D
C

69. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
BC = (−5−(−2)) +(2 −(−1)) = (−3) +(3)
A
B = 9+ 9 = 18
D
C

70. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
BC = (−5−(−2)) +(2 −(−1)) = (−3) +(3)
A
B = 9+ 9 = 18 units
D
C

71. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
BC = (−5−(−2)) +(2 −(−1)) = (−3) +(3)
A
B = 9+ 9 = 18 units
D
2 2
AD = (2 −5) +(4 −1)
C

72. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
BC = (−5−(−2)) +(2 −(−1)) = (−3) +(3)
A
B = 9+ 9 = 18 units
D
2 2 2 2
AD = (2 −5) +(4 −1) = (−3) +(3)
C

73. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
BC = (−5−(−2)) +(2 −(−1)) = (−3) +(3)
A
B = 9+ 9 = 18 units
D
2 2 2 2
AD = (2 −5) +(4 −1) = (−3) +(3)
C
= 9+ 9

74. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
BC = (−5−(−2)) +(2 −(−1)) = (−3) +(3)
A
B = 9+ 9 = 18 units
D
2 2 2 2
AD = (2 −5) +(4 −1) = (−3) +(3)
C
= 9+ 9 = 18

75. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
BC = (−5−(−2)) +(2 −(−1)) = (−3) +(3)
A
B = 9+ 9 = 18 units
D
2 2 2 2
AD = (2 −5) +(4 −1) = (−3) +(3)
C
= 9+ 9 = 18 units

76. Example 3
The vertices of quadrilateral ABCD are A = (2, 4), B = (-5, 2),
C = (-2, -1), and D = (5, 1).
b. Use distances to justify your guess.
2 2 2 2
BC = (−5−(−2)) +(2 −(−1)) = (−3) +(3)
A
B = 9+ 9 = 18 units
D
2 2 2 2
AD = (2 −5) +(4 −1) = (−3) +(3)
C
= 9+ 9 = 18 units
It is a parallelogram, as
opposite sides are equal.

77. Problem Set

78. Problem Set
p. 246 #1-33 odd, 18, 34, 36
“If I have seen further it is by standing on the shoulders of giants.”
- Isaac Newton