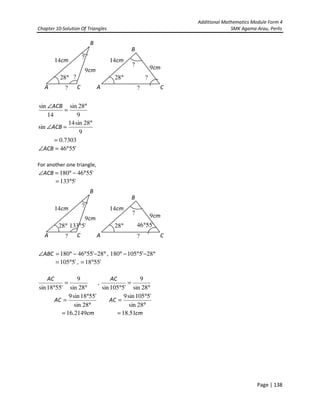
This document provides information about solving triangles using trigonometric ratios (sine rule and cosine rule) and calculating areas of triangles. It includes examples of using the sine rule and cosine rule to calculate missing side lengths and angles of triangles. It also discusses the formula for calculating the area of any triangle using sine of the angles and side lengths. Exercises are provided for students to practice applying these concepts and formulas to solve multi-step triangle problems.

1. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 132
CHAPTER 10- SOLUTION OF TRIANGLES
10.1 SINE RULE
10.1.1 Verifying the sine rule
(1)
Compare and ,
BcCb sinsin =
c
C
b
B sinsin
= or
C
c
B
b
sinsin
=
A
CB a
c b
B
A
D
Bch
B
c
h
sin
sin
=
=
D
A
C
Cbh
C
b
h
sin
sin
=
=
b
h
h
c
1 2
1
2
h
D

2. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 133
(2)
Compare and ,
CaAc sinsin =
c
C
a
A sinsin
= or
C
c
A
a
sinsin
=
From the first solution we know that
c
C
b
B sinsin
= or
C
c
B
b
sinsin
=
From the second solution we know that
c
C
a
A sinsin
= or
C
c
A
a
sinsin
=
Hence,
or
or
A
CB a
c
b
E
A
B
E
c
t
Act
A
c
t
sin
sin
=
=
Cct
C
a
t
sin
sin
=
=
B
E
Ca
t
1
2
1 2
c
C
b
B
a
A sinsinsin
==
C
c
B
b
A
a
sinsinsin
==

3. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 134
10.1.2 Using the sine rule
Example 1:
The diagram above shows a triangle ABC.
Calculate
(a) the length of BC
(b) the length of AC
Solution:
From the given information, we know that
°−°−°=∠ 4060180ACB
°= 80
(a) Using the sine rule,
°
°
=
°
=
°
80sin
60sin5
80sin
5
60sin
BC
BC
cm3969.4=
(b) Using the sine rule,
°
°
=
°
=
°
80sin
40sin5
80sin
5
40sin
BC
AC
cm2635.3=
A
C
B
°60
cm5
°40

4. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 135
Example 2:
The diagram above shows a triangle ABC.
Calculate
(a) BAC∠
(b) the length of AC
(a) Using the sine rule,
12
135sin8
sin
12
135sin
8
sin
°
=∠
°
=
∠
BAC
BAC
4714.0=
)4714.0(sin 1−
=∠BAC
'828°=
(b) At first, calculate the angle ABC∠
'828135180 °−°−°=∠ABC
'5216°=
Using the sine rule,
°
°
=
°
=
°
135sin
'5216sin12
135sin
12
'5216sin
AC
AC
cm9239.4=
°135
C
cm8
cm12 BA

5. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 136
EXERCISE 10.1
1. ABC is a triangle where cmAB 12= , cmAC 8= and °=∠ 30ABC . Find two possible values of
CAB∠
2. In diagram below, KLM is a straight line.
Calculate
(a) JLK∠
(b) LJM∠
3. In diagram below, ABC and BED are straight lines, E is the mid-point of BD.
Given that 7.0sin =∠CBD , calculate
(a) the length of BC
(b) BEA∠
4. Find the value of θ in each of the following triangles.
(a) (b)
J
K M
cm12
cm8 L
cm20
A
B
C
cm6.6
E D
cm8.9
A
C
B
°40
cm9
cm6
θ
θ
cm4.4
cm7.6
°35
P
R
Q

6. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 137
10.2 AN AMBIGUOUS CASE
An ambiguous case occurs when A∠ , length of AC are fixed. While a < b.
There are two possible triangles that can be constructed.
Example:
ABC is a triangle with °=∠ 28A . AB= 14 cm and BC= 9cm. Solve the triangle.
Solution:
To solve the triangle, we have to find ABC∠ , ACB∠ and the length of AC.
There are two possible triangles that can be constructed.
A
C
2B
b aa
1B
A
C
b
a
B
b a
A
C
B
A
B
C
cm14 cm9
°28
A 2C
cm14 cm9
°28
cm9
B
1C

7. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 138
9
28sin14
sin
9
28sin
14
sin
°
=∠
°
=
∠
ACB
ACB
7303.0=
'5546°=∠ACB
For another one triangle,
'5546180 °−°=∠ACB
'5133°=
°−°−°=∠ 28'5546180ABC , °−°−° 28'5105180
'5105°= , '5518°=
°
=
° 28sin
9
'5518sin
AC
,
°
=
° 28sin
9
'5105sin
AC
°
°
=
28sin
'5518sin9
AC
°
°
=
28sin
'5105sin9
AC
cm2149.16= cm51.18=
A
B
cm14
cm9
C
cm14
cm9
A
B
C
?
?
??
°28 °28
A
cm14
cm9
C
cm14
cm9
A
B
C
?
?
??
°28 °28'5133° '5546°
B
? ?

8. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 139
EXERCISE 10.2
1. Diagram below shows triangle PQR.
Calculate:
(a) the length of PQ
(b) The new length of PR if the lengths PQ, QR and QPR∠ are maintained.
2. Diagram below shows two triangles ABC and CDE. The two triangles are joined at C such that AE and
BD are straight lines. The CED∠ is an obtuse angle.
(a) Calculate
(i) ACB∠
(ii) DEC∠
(b) The straight line CE is extended to F such that DE = DF.
Find the area of triangle CDF.
°130
R
Q
P
cm2.6
cm8.4
cm5.6
cm9
cm4
cm5
cm7
E
DCB
A

9. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 140
10.3 COSINE RULE
10.3.1 Verifying the cosine rule
Substitute and into ,
)cos(2222
Bcacab −+=
Hence,
A
CB
a
c bh
D
x xa −
B
A
D
Bcx
B
c
x
cos
cos
=
=
h
c
1
x
222
hxc += 2
D
A
C
222
)( xahb −+=
b
h
3
xa −
axxha
axxah
2
2
222
222
−++=
−++=
1 2 3
Cabbac
Baccab
Abccba
cos2
cos2
cos2
222
222
222
−+=
−+=
−+=

10. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 141
EXERCISE 10.3
1. Given a triangle ABC, AB = 7.3 cm, AC = 9.3 cm and °=∠ 65CAB . Calculate the length of BC.
2. Given a triangle PQR, PQ = 7 cm, QR = 9 cm and PR = 15 cm. Calculate the length of PQR∠ .
3. Diagram below shows a triangle PQR.
Calculate PQR∠ .
4. In diagram below, KMN is an equilateral triangle. H is the midpoint of KN and KL = 8 cm.
Caclulate
(a) the length of LH
(b) KLH∠
5.
In diagram above, calculate
(a) the length of PR
(b) the value of x.
K
M
L
H
cm12
cm8
N
P
S
Q
cm12
cm7.10
R
cm8
x
P
Q
cm13
R
cm10
cm12

11. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 142
10.4 AREA OF TRIANGLE
A
c b
h
B a C
Cbh
b
h
SinC
sin=
=
BCh
AB
h
SinA
sin=
=
haArea ××=
2
1
Substitute into ,
CbaArea sin
2
1
××=
Cab sin
2
1
=
Substitute into ,
BcaArea sin
2
1
××=
Bsin
2
1
ac=
Hence,
1
2
1 3
CabArea sin
2
1
=
BacArea sin
2
1
=
AbcArea sin
2
1
=
The formula for area of triangle that is
heightbase ××
2
1
can only be used in
situation where there is right angle triangle.
In the situations that the triangle is not a
right-angled triangle, we cannot use the
formula.
This formula can be used to find the area of
all types of triangle as long as there is
enough information given. The sine of an
angle is multiplied by the length of line that
joining to form the angle. For example, sine
A is multiply by AB and AC that are the lines
that joining to form the angle A.
3
2 3

12. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 143
EXERCISE 10.4
1. PQR is a triangle where PQ = 7.3 cm, QR = 9.6 cm and PR = 14.7 cm.
Calculate
(a) the area of PQR∆
(b) the height of P from QR
2.
In diagram above, calculate the area of triangle ABC.
3. In diagram below, BCD is a straight line.
Calculate
(a) ACD∠
(b) the length of AB
(c) the area of ABC∆
CHAPTER REVIEW EXERCISE
1. The diagram shows a triangle ABC.
(a) If the length of PQ and PR and the size of ACB∠ are
maintained, sketch and label another triangle
different from ABC∆ in the figure.
(b) Calculate the two possible values of BC.
A
B
cm6.10
cm7.5C
cm5.6
°73
D
B
A
cm9.10
C
cm2.8
cm4.6
A
B C
cm2.9
cm5.6
°33

13. Additional Mathematics Module Form 4
Chapter 10-Solution Of Triangles SMK Agama Arau, Perlis
Page | 144
2.
In diagram above,
6
5
sin =∠PSR where PSR∠ is an obtuse angle. Calculate
(a) the length of PR, correct to two decimal places
(b) PQR∠
(c) the area of the whole diagram
3. Diagram below shows triangle ABC and triangle AED. AEC is a straight line.
Given that °=∠ 60BAC , AB = 5 cm. BC = 8 c,. AE = 8.5 cm an ED = 15.6 cm.
Calculate
(a) the length of EC
(b) AED∠ , if the area of triangle AED is 54 cm2
.
4. Diagram below shows a right prism with an isosceles triangular base where DE =DF = 10 cm.
FE = 8 cm and AD = 7 cm.
Calculate
(a) the angle between the line AE and the base FED
(b) FAE∠
R
Q
P
S
cm6
cm10
cm15
°40
A
D
B
E
C
cm5
cm5.8
cm8
cm6.15
F
C
A
E
D
cm7
cm8 cm10