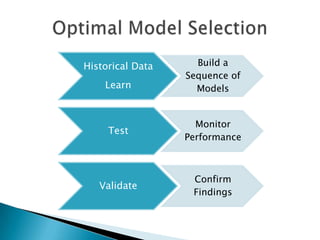
This document provides an overview of data mining concepts and techniques. It discusses topics such as predictive analytics, machine learning, pattern recognition, and artificial intelligence as they relate to data mining. It also covers specific data mining algorithms like decision trees, neural networks, and association rules. The document discusses supervised and unsupervised learning approaches and explains model evaluation techniques like accuracy, ROC curves, gains/lift curves, and cross-entropy. It emphasizes the importance of evaluating models on test data and monitoring performance over time as patterns change.

1. Dan Steinberg
N Scott Cardell
Mykhaylo Golovnya
November, 2011
Salford Systems

3. Data Mining Data Mining Cont.
• Predictive Analytics • Statistics • OLAP
• Machine Learning • Computer science • CART
• Pattern Recognition • Database • SVM
• Artificial Management • NN
Intelligence • Insurance • CRISP-DM
• Business • Finance • CRM
Intelligence • Marketing • KDD
• Data Warehousing • Electrical • Etc.
Engineering
• Robotics
• Biotech and more

4.  Data mining is the search for patterns in data
using modern highly automated, computer
intensive methods
◦ Data mining may be best defined as the use of a specific
class of tools (data mining methods) in the analysis of
data
◦ The term search is key to this definition, as is
“automated”
 The literature often refers to finding hidden
information in data

5. • Study the phenomenon
• Understand its nature
Science • Try to discover a law
• The laws usually hold for a long time
•Collect some data
•Guess the model (perhaps, using science)
Statistics •Use the data to clarify and/or validate the model
•If looks “fishy”, pick another model and do it
again
• Access to lots of data
• No clue what the model might be
Data Mining • No long term law is even possible
• Let the machine build a model
• And let‟s use this model while we can

6.  Quest for the Holy Grail- build an algorithm that will
always find 100% accurate models
 Absolute Powers- data mining will finally find and
explain everything
 Gold Rush- with the right tool one can rip the stock-
market and become obscenely rich
 Magic Wand- getting a complete solution from start
to finish with a single button push
 Doomsday Scenario- all conventional analysts will
eventually be replaced by smart computer chips

7.  This is known as “supervised learning”
◦ We will focus on patterns that allow us to accomplish two tasks
 Classification
 Regression
 This is known as “unsupervised learning”
◦ We will briefly touch on a third common task
 Finding groups in data (clustering, density estimation)
 There are other patterns we will not discuss today
including
◦ Patterns in sequences
◦ Connections in networks (the web, social networks, link analysis)

8.  CART® (Decision Trees, C4.5, CHAID among others)
 MARS® (Multivariate Adaptive Regression Splines)
 Artificial Neural Networks (ANNs, many commercial)
 Association Rules (Clustering, market basket analysis)
 TreeNet® (Stochastic Gradient Tree Boosting)
 RandomForests® (Ensembles of trees w/ random splits)
 Genetic Algorithms (evolutionary model development)
 Self Organizing Maps (SOM, like k-means clustering)
 Support Vector Machine (SVM wrapped in many patents)
 Nearest Neighbor Classifiers

9.  (Insert chart)
 In a nutshell: Use historical data to gain
insights and/or make predictions on the new
data

10.  Given enough learning iterations, most data mining methods are
capable of explaining everything they see in the input
data, including noise
 Thus one cannot rely on conventional (whole sample) statistical
measures of model quality
 A common technique is to partition historical data into several
mutually exclusive parts
◦ LEARN set is used to build a sequence of models varying in size and level
of explained details
◦ TEST set is used to evaluate each candidate model and suggest the
optimal one
◦ VALIDATE set is sometimes used to independently confirm the optimal
model performance on yet another sample

11. Historical Data Build a
Sequence of
Learn Models
Monitor
Test
Performance
Confirm
Validate
Findings

12.  Analyst needs to indicate where the TEST data is to be
found
◦ Stored in a separate file
◦ Selected at random from the available data
◦ Pre-selected from available data and marked by a special indicator
 Other things to consider
◦ Population: LEARN and TEST sets come from different populations
(within-sample versus out-of-sample)
◦ Time: LEARN and TEST sets come from different time periods
(within-time versus out-of-time)
◦ Aggregation: logically grouped records must be all included or all
excluded within each set (self-correlation)

13.  Any model is built on past data!
 Fortunately, many models trace stable patterns of behavior
 However, any model will eventually have to be rebuilt:
◦ Banks like to refresh risk models about every 12 months
◦ Targeted marketing models are typically refreshed every 3 months
◦ Ad web-server models may be refreshed every 24 hours
 Credit risk score card expert Professor David
Hand, University of London maintains:
◦ A predictive model is obsolete the day it is first deployed

15.  Model evaluation is at the core of the learning process (choosing
the optimal model from a list of candidates)
 Model evaluation is also a key part in comparing performance of
different algorithms
 Finally, model evaluation is needed to continuously monitor
model performance over time
 In predictive modeling (classification and regression) all we need
is a sample of data with known outcome; different evaluation
criteria can then be applied
 There will never be “the best for all” model; the optimality is
contingent upon current evaluation criterion and thus depends
on the context in which the model is applied

16.  (insert graph)
 One usually computes some measure of average
discrepancy between the continuous model predictions f
and the actual outcome y
◦ Least Squared Deviation: R= Σ(y-f)^2
◦ Least Absolute Deviation: R= Σ Iy-fI
 Fancier definitions also exist
◦ Huber-M Loss: is defined as a hybrid between the LS and LAD
losses
◦ SVM Loss: ignores very small discrepancies and then switches to
LAD-style
 The raw loss value is often re-expressed in relative terms
as R-squared

17.  There are three progressively more demanding approaches to
solving binary classification problems
 Division: a model makes the final class assignment for each
observation internally
◦ Observations with identical class assignment are no longer discriminated
◦ A model needs to be rebuilt to change decision rules
 Rank: a model assigns a continuous score to each observation
◦ The score on its own bears no direct interpretation
◦ But, higher class score means higher likelihood of class presence in
general (without precise quantitative statements)
◦ Any monotone transformation of scores is admissible
◦ A spectrum of decision rules can be constructed strictly based on varying
score threshold without model rebuilding
 Probability: a model assigns a probability score to each observation
◦ Same as above, but the output is interpreted directly in the exact probabilistic
terms

18.  Depending on the prediction emphasis, various performance evaluation
criteria can be constructed for binary classification models
 The following list, far from being exhausting, presents some of the
frequently used evaluation criteria
◦ Accuracy (more generally- Expected Cost)
 Applicable to all models
◦ ROC Curve and Area Under Curve
 Not Applicable to Division Models
◦ Gains and Lift
 Not Applicable to Division Models
◦ Log-likelihood (a.k.a Cross-Entropy, Deviate)
 Not Applicable to Division and Rank Models
 The criteria above are listed in the order from the least specific to the
most
 It is not guaranteed that all criteria will suggest the same model as the
optimal from a list of candidate models

19.  Most intuitive and also the weakest evaluation method that can be
applied to any classification model
 Each record must be assigned to a specific class
 One first constructs a Prediction Success Table- a 2 by 2 matrix showing
how many true 0s and 1s (rows) were classified by the model correctly or
incorrectly (columns)
 The classification accuracy is then the number of correct class
assignments divided by the sample size
 More general approaches will also include user supplied prior
probabilities and cost matrix to compute the Expected Cost
 The example below reports prediction success tables for two separate
models along with the accuracy calculations
 The method is not sensitive enough to emphasize larger class unbalance
in model 1
 (insert table)

20.  The classification accuracy approach assumes that each record
has already been classified which is not always convenient
◦ Those algorithms producing a continuous score (Rank or Probability) will
require a user-specified threshold to make final class assignments
◦ Different thresholds will result to different class assignments and likely
different classification accuracies
 The accuracy approach focuses on the separating boundary and
ignores fine probability structure outside the boundary
 Ideally, need an evaluator working directly with the score itself
and not dependent on any external considerations like costs and
thresholds
 Also, for Rank models the evaluator needs to be invariant with
respect to monotone transformation of the scores so that the
“spirit” of such models is not violated

21.  The following approach will take full advantage of the set of
continuous scores produced by Rank or Probability models
 Pick one of the two target classes as the class in focus
 Sort a database by predicted score in descending order
 Choose a set of different score values
◦ Could be ALL of the unique scores produced by the model
◦ More often a set of scores obtained by binning sorted records into equal
size bins
 For any fixed value of the score we can now compute:
◦ Sensitivity (a.k.a True Positive): Percent of the class in focus with the
predicted scores above the threshold
◦ Specificity (a.k.a False Positive): Percent of the opposite class with the
predicted scores below the threshold
 We then display the results as a plot of [sensitivity] versus [1-specificity]
 The resulting curve is known as the ROC Curve

22.  (insert graph)
 ROC Curves for three different rank models are shown
 No model can be considered as the absolute best in all times
 The optimal model selection will rest with the user
 Average overall performance can be measured as Area Under
ROC Curve (AUC)
◦ ROC Curve (up to orientation) and AUC are invariant with respect to the
focus class selection
◦ The best attainable AUS is always 1.0
◦ AUC of a model with randomly assigned scores is 0.5
 AUC can be interpreted
◦ Suppose we randomly and repeatedly pick one observation at random
from the focus class and another observation from the opposite class
◦ Then AUC is the fraction of trials resulting to the focus class observation
having greater predicted score than the opposite class observation
◦ AUC below 0.5 means that something is fundamentally wrong

23.  The following example justifies another slightly different approach to model
evaluation
 Suppose we want to mail a certain offer to P fraction of the population
 Mailing to a randomly chosen sample will capture about P fraction of the
responders (random sampling procedure)
 Now suppose that we have access to a response model which ranks each potential
responder by a score
 Now if we sample the P fraction of the population targeting members with the
highest predicted scores first (model guided sampling), we could now get T
fraction of the responders which we expect to be higher than P
 The lift in P(th) percentile is defined as the ratio T/P
 Obviously, meaningful models will always produce lift greater than 1
 The process can be repeated for all possible percentiles and the results can be
summarized graphically as Gains and Cumulative Lift curves
 In practice, one usually first sorts observations by scores and then partitions
sorted data into a fixed number of bins to save on calculations just like it is
usually done for ROC curves

24.  (insert graphs and tables)

25.  (insert graphs)
 Lift in the given percentile provides a point measure of
performance for the given population cutoff
◦ Can be viewed as the relative length of the vertical line segment
connecting the gains curve at the given population cutoff
 Area Under the Gains curve (AUG): Provides an integral measure
of performance across all bins
◦ Unlike AUC, the largest attainable value of AUG is (1-p/2), P being the
fraction of responders in the population
 Just like ROC-curves, gains and lift curves for different models
can intersect, so that performance-wise one model is better for
one range of cutoffs while another model is better for a different
range
 Unlike ROC-curve, gains and lift curves do depend on the class
in focus
◦ For the dominant class, gains and lift curves degenerate to the trivial 45-
degree line random case

26.  ROC, Gains, and lift curves together with AUC and AUG are invariant
with respect to monotone transformation of the model scores
◦ Scores are only used to sort records in the evaluation set, the actual score
values are of no consequence
 All these measures address the same conceptual phenomenon
emphasizing different sides and thus can be easily derived from
each other
◦ Any point (P,G) on a gains curve corresponds to the point (P,G/P) on the
lift curve
◦ Suppose that the focus class occupies fraction F of the population; then
any point (P,G) on a gains curve corresponds to the point {(P-FG)/(1-F),G}
on the ROC curve
 It follows that the ROC graph “pushes” the gains graph “away” from the 45
degree line
 Dominant focus class (large F) is “pushed” harder so that the degeneracy of
its gain curve disappears
 In contrast, rare focus class (small F) has ROC curve naturally “close” to the
gains curve
 All of these measures are widely used as robust performance
evaluations in various practical applications

27.  When the output score can be interpreted as probability, a more specific
evaluation criterion can be constructed to access probabilistic accuracy
of the model
 We assume that the model generates P(X)-the conditional probability of
1 given X
 We also assume that the binary target Y is coded as -1 and +1 (only for
notational convenience)
 The Cross-Entropy (CXE) criterion is then computed as (insert equation)
◦ The inner Log computes the log-odds of Y=1
◦ The value itself is the negative log-likelihood assuming independence of
responses
◦ Alternative notation assumes 0/1 target coding and uses the following
formula (insert equation)
◦ The values produced by either of the formula will be identical to each
other
 Model with the smallest CXE means the largest likelihood and thus
considered to be the best in terms of capturing the right probability
structure

28.  The example shows true non-monotonic conditional probability
(dark blue curve)
 We generated 5,000 LEARN and TEST observations based on this
probability model
 We report predicted responses generated by different modeling
approaches
◦ Red- best accuracy MART model
◦ Yellow- best CXE MART model
◦ Cyan- univariate LOGIT model
 Performance-wise
◦ All models have identical accuracy but the best accuracy model is
substantially worse in terms of CXE
◦ LOGIT can‟t capture departure from monotonicity as reported by CXE

30.  MARS is a highly-automated tool for regression
 Developed by Jerome H. Friedman of Stanford University
◦ Annals of statistics, 1991 dense 65 page article
◦ Takes some inspiration from its ancestor CART®
◦ Produces smooth curves and surfaces, not the step-functions of CART
 Appropriate target variables are continuous
 End result of a MARS run is a regression model
◦ MARS automatically chooses which variables to use
◦ Variables are optimally transformed
◦ Interactions are detected
◦ Model is self-tested to protect against over-fitting
 Can also perform well on binary dependent variables
◦ Censored survival model (waiting time models as in churn)

31.  Harrison, D. and D. Rubinfeld.
Hedonic Housing Prices and Demand for Clean Air. Journal of
Environmental Economics and Management v5, 81-102, 1978
 506 census tracts in city of Boston for the year 1970
 Goal: study relationship between quality of life variables and property
values
◦ MV- median value of owner-occupied homes in tract („000s)
◦ CRIM- per capita crime rates
◦ NOX- concentration of nitrogen oxides (pphm)
◦ AGE- percent built before 1940
◦ DIS- weighted distance to centers of employment
◦ RM- average number of rooms per house
◦ LSTAT- percent neighborhood „lower socio-economic status‟
◦ RAD- accessibility to radial highways
◦ CHAS- borders Charles River (0/1)
◦ INDUS- percent non-retail business
◦ TAX- tax rate
◦ PT- pupil teacher ratio

32.  (insert graph)
 The dataset poses significant challenges to
conventional regression modeling
◦ Clearly departure from normality, non-linear
relationships, and skewed distributions
◦ Multicollinearity, mutual dependency, and outlying
observations

33.  (insert graph)
 A typical MARS solution (univariate for simplicity)
is shown above
◦ Essentially a piece-wise linear regression model with the
continuity requirement at the transition points called
knots
◦ The locations and number of knots were determined
automatically to ensure the best possible model fit
◦ The solution can be analytically expressed as
conventional regression equations

34.  Finding the one best knot in a simple regression is a straightforward
search problem
◦ Try a large number of potential knots and choose one with the best R-
squared
◦ Computation can be implemented efficiently using update algorithms;
entire regression does not have to be rerun for every possible knot (just
update X‟X matrices)
 Finding k knots simultaneously would require n^k order of
computations assuming N observations
 To preserve linear problem complexity, multiple knot
replacement is implemented in a step-wise manner:
◦ Need a forward/backward procedure
◦ The forward procedure adds knots sequentially one at a time
 The resulting model will have many knots and overfit the training data
◦ The backward procedure removes least contributing knots one at a time
 This produces a list of models of varying complexity
◦ Using appropriate evaluation criterion, identify the optimal model
 Resulting model will have approximately correct knot locations

35.  (insert graphs)
 True conditional mean has two knots at X=30
and X=60, observed data includes additional
random error
 Best single knot will be at X=45, subsequent best
locations are true knots around 30 and 60
 The backward elimination step is needed to
remove the redundant node at X=45

36.  Thinking in terms of knot selection works very well to
illustrate splines in one dimension but unwieldy for
working with a large number of variables simultaneously
◦ Need a concise notation easy to program and extend in multiple
dimensions
◦ Need to support interactions, categorical variables, and missing
values
 Basis functions (BF) provide analytical machinery to
express the knot placement strategy
 Basis function is a continuous univariate transform that
reduces predictor influence to a smaller range of values
controlled by a parameter c (20 in the example below)
◦ Direct BF: max(X-c, 0)- the original range is cut below c
◦ Mirror BF: max (c-X, 0)- the original range is cut above c
◦ (insert graphs)

37.  The following model represents a 3-knot
univariate solution for the Boston Housing
Dataset using two direct and one mirror basis
functions
 (insert equations)
 All three line segments have negative slope
even though two coefficients are above zero
 (insert graph)

38.  MARS core technology:
◦ Forward step: add basis function pairs one at a time in conventional step-
wise forward manner until the largest model size (specified by the user) is
reached
 Possible collinearity due to redundancy in pairs must be detected and
eliminated
 For categorical predictors define basis functions as indicator variables for all
possible subsets of levels
 To support interactions, allow cross products between a new candidate pair
and basis functions already present in the model
◦ Backward step: remove basis functions one at a time in conventional step-
wise backward manner to obtain a sequence of candidate models
◦ Use test sample or cross-validation to identify the optimal model size
 Missing values are treated by constructing missing value
indicator (MVI) variables and nesting the basis functions within
the corresponding MVIs
 Fast update formulae and smart computational shortcuts exist to
make the MARS process as fast and efficient as possible

39.  OLS and MARS regression (insert graphs)
 We compare the results of classical linear regression
and MARS
◦ Top three significant predictors are shown for each model
◦ Linear regression provides global insights
◦ MARS regression provides local insights and has superior
accuracy
 All cut points were automatically discovered by MARS
 MARS model can be presented as a linear regression model in
the BF space

41.  One of the oldest Data Mining tools for classification
 The method was originally developed by Fix and Hodges (1951) in an
unpublished technical report
 Later on it was reproduced by Agrawala (1977), Silverman and Jones
(1989)
 A review book with many references on the topic is Dasarathy (1991)
 Other books that treat the issue:
◦ Ripley B.D. 1996. Pattern Recognition and Neural Networks (chapter 6)
◦ Hastie T, Tibshirani R and Friedman J. 2001. The Elements of Statistical Learning Data
Mining, Inference and Prediction (chapter 13)
 The underlying idea is quite simple: make the predictions by proximity
or similarity
 Example: we are interested in predicting if a customer will respond to an
offer. A NN classifier will do the following:
◦ Identify a set of people most similar to the customer- the nearest neighbor
◦ Observe what they have done in the past on a similar offer
◦ Classify by majority voting: if most of them are responders, predict a
responder, otherwise, predict a non-responder

42.  (insert graphs)
 Consider binary classification problem
 Want to classify the new case highlighted in yellow
 The circle contains the nearest neighbors (the most similar
cases)
◦ Number of neighbors= 16
◦ Votes for blue class= 13
◦ Votes for red class= 3
 Classify the new case in the blue class. The estimated probability
of belonging to the blue class is 13/16=0.8125
 Similarly in this example:
◦ Classify the yellow instance in the blue class
◦ Classify the green instance in the red class
◦ The black point receives three votes from the blue class and another three
from the red one- the resulting classification is indeterminate

43.  There are two decisions that should be made in advance before
applying the NN classifier
◦ The shape of the neighborhood
 Answers the question “Who are our nearest neighbors?”
◦ The number of neighbors (neighborhood size)
 Answers the question “How many neighbors do we want to consider?”
 Neighborhood shape amounts to choosing the
proximity/distance measure
◦ Manhattan distance
◦ Euclidean distance
◦ Infinity distance
◦ Adaptive distances
 Neighborhood size K can vary between 1 and N (the dataset size)
◦ K=1-classification is based on the closest case in the dataset
◦ K=N-classification is always to the majority class
◦ Thus K acts as a smoothing parameter and can be determined by using a
test sample or cross-validation

44.  NN advantages
◦ Simple to understand and easy to implement
◦ The underlying idea is appealing and makes logical sense
◦ Available for both classification and regression problems
 Predictions determined by averaging the values of nearest neighbors
◦ Can produce surprisingly accurate results in a number of
applications
 NN have been proved to perform equal or better than LDA, CART, Neural
Networks and other approaches when applied to remote sensed data
 NN disadvantages
◦ Unlike decision trees, LDA, or logistic regression, their decision
boundaries are not easy to describe and interpret
◦ No variable selection of any kind- vulnerable to noisy inputs
 All the variables have the same weight when computing the distance, so
two cases could be considered similar (or dissimilar) due to the role of
irrelevant features (masking effects)
◦ Subject to the curse of dimensionality in high dimension datasets
◦ The technique is quite time consuming. However, Friedman et. Al.
(1975 and 1977) have proposed fast algorithms

46.  Classification and Regression Trees (CART®)- original approach
based on the “let the data decide local regions” concept
developed by Breiman, Friedman, Olshen, and Stone in 1984
 The algorithm can be summarized as:
◦ For each current data region, consider all possible orthogonal splits (based
on one variable) into 2 sub-regions
◦ The best split is defined as the one having the smallest MSE after fitting a
constant in each sub-region (regression) or the smallest resulting class
impurity (classification)
◦ Proceed recursively until all structure in the training set has been
completely exhausted- largest tree is produced
◦ Create a sequence of nested sub-trees with different amount of
localization (tree pruning)
◦ Pick the best tree based on the performance on a test set or cross-
validated
 One can view CART tree as a set of dynamically constructed
orthogonal nearest neighbor boxes of varying sizes guided by
the response variable (homogeneity of response within each box)

47.  CART is best illustrated with a famous example- the UCSD Heart
Disease study
◦ Given the diagnosis of a heart attack based on
 Chest pain, Indicative EKGs, Elevation of enzymes typically released by
damaged heart muscle, etc.
◦ Predict who is at risk of a 2nd heart attack and early death within 30 days
◦ Prediction will determine treatment program (intensive care or not)
 For each patient about 100 variables were available, including:
◦ Demographics, medical history, lab results
◦ 19 noninvasive variables were used in the analysis
 Age, gender, blood pressure, heart rate, etc.
 CART discovered a very useful model utilizing only 3 final
variables

48.  (insert classification tree)
 Example of a CLASSIFICATION tree
 Dependent variable is categorical (SURVIVE, DIE)
 The model structure is inherently hierarchical and cannot be represented
by an equivalent logistic regression equation
 Each terminal node describes a segment in the population
 All internal splits are binary
 Rules can be extracted to describe each terminal node
 Terminal node class assignment is determined by the distribution of the
target in the node itself
 The tree effectively compresses the decision logic

49.  CART advantages:
◦ One of the fastest data mining algorithms available
◦ Requires minimal supervision and produces easy to understand
models
◦ Focuses on finding interactions and signal discontinuities
◦ Important variables are automatically identified
◦ Handles missing values via surrogate splits
 A surrogate split is an alternative decision rule supporting the main rule
by exploiting local rank-correlation in a node
◦ Invariant to monotone transformations of predictors
 CART disadvantages:
◦ Model structure is fundamentally different from conventional
modeling paradigms- may confuse reviewers and classical
modelers
◦ Has limited number of positions to accommodate available
predictors- ineffective at presenting global linear structure (but
great for interactions)
◦ Produces coarse-grained piece-wise constant response surfaces

50.  (insert charts)
 10-node CART tree was built on the cell phone dataset
introduced earlier
 The root Node 1 displays details of TARGET variable in the
training data
◦ 15.2% of the 830 households accepted the marketing offer
 CART tried all variable predictors one at a time and found out
that partitioning the set of subjects based on the Handset Price
variable is most effective at separating responders from non-
responders at this point
◦ Those offered the phone with a price>130 contain only 9.9% responders
◦ Those offered a lower price<130 respond at 21.9%
 The process of splitting continues recursively until the largest
tree is grown
 Subsequent tree pruning eliminates least important branches
and creates a sequence of nested trees- candidate models

51.  (insert charts)
 The red nodes indicate good responders while the blue nodes
indicate poor responders
 Observations with high values on a split variable always go right
while those with low values go left
 Terminal nodes are numbered left to right and provide the
following useful insights
◦ Node 1: young prospects having very small phone bill, living in specific
cities are likely to respond to an offer with a cheap handset
◦ Node 5: mature prospects having small phone bill, living in specific cities
(opposite Node1) are likely to respond to an offer with a cheap handset
◦ Nodes 6 and 8: prospects with large phone bill are likely to respond as
long as the handset is cheap
◦ Node 10: “high-tech” prospects (having a pager) with large phone bill are
likely to respond to even offers with expensive handset

52.  (insert graph, table and chart)
 A number of variables were identified as
important
◦ Note the presence of surrogates not seen on the main
tree diagram previously
 Prediction Success table reports classification
accuracy on the test sample
 Top decile (10% of the population with the
highest scores) captures 40% of the responders
(lift of 4)

53.  (insert graphs)
 CART has a powerful mechanism of priors built
into the core of the tree building mechanism
 Here we report the results of an experiment with
prior on responders varying from 0.05 to 0.95 in
increments of 0.05
 The resulting CART models “sweep” the modeling
space enforcing different sensitivity-specificity
tradeoff

54.  As prior on the given class decreases
 The class assignment threshold increases
 Node richness goes up
 But class accuracy goes down
 PRIORS EQUAL uses the root node class ratio as the class assignment
threshold- hence, most favorable conditions to build a tree
 PRIORS DATA uses the majority rule as the class assignment threshold-
hence, difficult modeling conditions on unbalanced classes.
 In reality, a proper combination of priors can be found experimentally
 Eventually, when priors are too extreme, CART will refuse to build a tree.
◦ Often the hottest spot is a single node in the tree built with the most
extreme priors with which CART will still build a tree.
◦ Comparing hotspots in successive trees can be informative, particularly in
moderately-sized data sets.

55.  (insert graph)
 We have a mixture of two overlapping classes
 The vertical lines show root node splits for
different sets of priors. (the left child is classified
as red, the right child is classified as blue)
 Varying priors provides effective control over the
tradeoff between class purity and class accuracy

56.  Hot spots are areas of data very rich in the event of interest, even
though they could only cover a small fraction of the targeted
group
◦ A set of prospects rich in responders
◦ A set of transactions with abnormal amount of fraud
 The varying-priors collection of runs introduced above gives
perfect raw material in the search of hot spots
◦ Simply look at all terminal nodes across all trees in the collection and
identify the highest response segments
◦ Also want to have such segments as large as possible
◦ Once identified, the rules leading to such segments (nodes) are easily
available
◦ (insert graph)
◦ The graph on the left reports all nodes according to their target coverage
and lift
◦ The blue curve connects the nodes most likely to be a hot spot

57.  (insert graph)
 Our next experiment (variable shaving) runs as follows:
◦ Build a CART model with the full set of predictors
◦ Check the variable importance, remove the least important
variable and rebuild CART model
◦ Repeat previous step until all variables have been removed
 Six-variable model has the best performance so far
 Alternative shaving techniques include:
◦ Proceed by removing the most important variable- useful in
removal of model “hijackers”- variables looking very strong on the
train data but failing on the test data (e.g. ID variables)
◦ Set up nested looping to remove redundant variables from the
inner positions on the variable importance list

58.  (insert tree)
 Many predictive models benefit from Salford Systems
patent on “Structured Trees”
 Trees constrained in how they are grown to reflect
decision support requirements
◦ Variables allowed/disallowed depending on a level in a tree
◦ Variable allowed/disallowed depending on a node size
 In mobile phone example: want tree to first segment on
customer characteristics and then complete using price
variables
◦ Price variables are under the control of the company
◦ Customer characteristics are beyond company control

59.  Various areas of research were spawned by CART
 We report on some of the most interesting and well developed
approaches
 Hybrid models
◦ Combining CART with linear and Logistic Regression
◦ Combining CART with Neural Nets
 Linear combination splits
 Committees of trees
◦ Bagging
◦ Arcing
◦ Random Forest
 Stochastic Gradient Boosting (MART a.k.a TreeNet)
 Rule Fit and Path Finder

61.  (insert images)
 Grow a tree on training data
 Find a way to grow another tree, different from currently
available (change something in set up)
 Repeat many times, say 500 replications
 Average results or create voting scheme
◦ For example, relate PD to fraction of trees predicting default for a given
 Beauty of the method is that every new tree starts with a
complete set of data
 Any one tree can run out of data, but when that happens we just
start again with a new tree and all the data (before sampling)

62.  Have a training set of size N
 Create a new data set of size N by doing sampling with
replacement from the training set
 The new set (called bootstrap sample) will be different from the
original:
◦ 36.5% of the original records are excluded
◦ 37.5% of the original records are included once
◦ 18% of the original records are included twice
◦ 6% of the original records are included three times
◦ 2% of the original records are included four or more times
 May do this repeatedly to generate numerous bootstrap samples
 Example: distribution of record weights in one realized bootstrap
sample
 (insert table)

63.  To generate predicted response, multiple trees are combined via
voting (classification) or averaging (regression) schemas
 Classification trees “vote”
◦ Recall that classification trees classify
 Assign each case to ONE class only
◦ With 100 trees, 100 separate class assignment (votes) for each record
◦ Winner is the class with the most votes
◦ Fraction of votes can be used as a crude approximation to class
probability
◦ Votes could be weighted- say by accuracy of individual trees or node sizes
◦ Class weights can be introduced to counter the effects of dominant classes
 Regression trees assign a real predicted value for each case
◦ Predictions are combined via averaging
◦ Results will be much smoother than from a single tree

64.  Breiman reports the results of running bootstrap
aggregation (bagger) on four publicly available
datasets from Statlog project
 In all cases the bagger shows substantial
improvement in the classification accuracy
 It all comes at a price of no longer having a
single interpretable model, substantially longer
run time and greater demand on model storage
space
 (insert tables)

65.  Bagging proceeds by independent, identically-distributed
sampling draws
 Adaptive resampling: probability that a case is sampled varies
dynamically
◦ Cases with higher current prediction errors have greater probability of
being sampled in the next round
◦ Idea is to focus on these cases most difficult to predict correctly
 Similar procedure first introduced by Freund & Schapire (1996)
 Breiman variant (ARC-x4) is easier to understand:
◦ Suppose we have already grown K trees: let m= # times case i was
misclassified (0≤m≤k) (insert equations)
◦ Weight=1 for cases with zero occurrences of misclassification
◦ Weight= 1+k^4 for cases with K misclassifications
 Weigh rapidly becomes large is case is difficult to classify

66.  The results of running bagger and ARCer on the Boston
Housing Data are reported below
 Bagger shows substantial improvement over the single-
tree model
 ARCer shows marginal improvement over the bagger
 (insert table)
 Single tree now performs worse than stand alone CART run
(R-squared=72%) because in bagging we always work with
exploratory trees only
 Arcing performance beats MARS additive model but is still
inferior to the MARS interactions model

67.  Boosting (and Bagging) are very slow and consume a lot of
memory, the final models tend to be awkwardly large and
unwieldy
 Boosting in general is vulnerable to overtraining
◦ Much better fit on training than on test data
◦ Tendency to perform poorly on future data
◦ Important to employ additional considerations to reduce overfitting
 Boosting is also highly vulnerable to errors in the data
◦ Technique designed to obsess over errors
◦ Will keep trying to “learn” patterns to predict miscoded data
◦ Ideally would like to be able to identify miscoded and outlying data and
exclude those records from the learning process
◦ Documented in study by Dietterich (1998)
 An Experimental Comparison of Three Methods for Constructing Ensembles
of Decision Trees, Bagging, Boosting, and Randomization

69.  New approach for many data analytical tasks developed by
Leo Breiman of University of California, Berkeley
◦ Co-author of CART® with Friedman, Olshen, and Stone
◦ Author of Bagging and Arcing approaches to combining trees
 Good for classification and regression problems
◦ Also for clustering, density estimation
◦ Outlier and anomaly detection
◦ Explicit missing value imputation
 Builds on the notions of committees of experts but is
substantially different in key implementation details

70.  A random forest is a collection of single trees grown in a
special way
◦ Each tree is grown on a bootstrap sample from the learning set
◦ A number R is specified (square root by defualt) such that is
noticeably smaller than the total number of available predictors
◦ During tree growing phase, at each node only R predictors are
randomly selected and tried
 The overall prediction is determined by voting (in
classification) or averaging (in regression)
 The law of Large Numbers ensures convergence
 The key to accuracy is low correlation and bias
 To keep bias low, trees are grown to maximum depth

71.  Randomness is introduced in two distinct ways
 Each tree is grown on a bootstrap sample from the learning set
◦ Default bootstrap sample size equals original sample size
◦ Smaller bootstrap sample sizes are sometimes useful
 A number R is specified (square root by default) such that it is
noticeably smaller than the total number of available predictors
 During tree growing phase, at each node only R predictors are
randomly selected and tried.
 Randomness also reduces the signal to noise ratio in a single
tree
◦ A low correlation between trees is more important than a high signal when
many trees contribute to forming the model
◦ RandomForests™ trees often have very low signal strength, even when the
signal strength of the forest is high.

72.  (insert graph)
 Gold- Average of 50 Base Learners
 Blue- Average of 100 Base Learners
 Red- Average of 500 Base Learners

73.  (insert graph)
 Averaging many base learners improves the
signal to noise ratio dramatically provided
that the correlation of errors is kept low
 Hundreds of base learners are needed for the
most noticeable effect

74.  All major advantages of a single tree are automatically preserved
 Since each tree is grown on a bootstrap sample, one can
◦ Use out of bag samples to compute an unbiased estimate of the accuracy
◦ Use out of bag samples to determine variable importances
 There is no overfitting as the number of trees increases
 It is possible to compute generalized proximity between any pair
of cases
 Based on proximities one can
◦ Proceed with a target-driven clustering solution
◦ Detect outliers
◦ Generate informative data views/projections using scaling coordinates
◦ Do missing value imputation
 Interesting approaches to expanding the methodology into
survival models and the unsupervised learning domain

75.  RF introduces a novel way to define proximity between two observations:
◦ For a dataset of size N define an NXN matrix of proximities
◦ Initialize all proximities to zeroes
◦ For any given tree, apply the tree to the dataset
◦ If case i and case j both end up in the same node, increase proximity
proxij between i and j by one
◦ Accumulate over all trees in RF and normalize by twice the number of trees
in RF
 The resulting matrix provides intrinsic measure of proximity
◦ Observations that are “alike” will have proximities close to one
◦ The closer the proximity to 0, the more dissimilar cases i and j are
◦ The measure is invariant to monotone transformations
◦ The measure is clearly defined for any type of independent
variables, including categorical

77.  TreeNet (TN) is a new approach to machine learning and function
approximation developed by Jerome H, Friedman at Stanford
University
◦ Co-author of CART® with Breiman, Olshen and Stone
◦ Author of MARS®, PRIM, Projection Pursuit, COSA, RuleFit™ and more
 Also known as Stochastic Gradient Boosting and MART (Multiple
Additive Regression Trees)
 Naturally supports the following classes of predictive models
◦ Regression (continuous target, LS and LAD loss functions)
◦ Binary Classification (binary target, logistic likelihood loss function)
◦ Multinomial classification (multiclass target, multinomial likelihood loss
function)
◦ Poisson regression (counting target, Poisson Likelihood loss function)
◦ Exponential survival (positive target with censoring)
◦ Proportional hazard cox survival model
 TN builds on the notions of committees of experts and boosting
but is substantially different in key implementation details

78.  We focus on TreeNet because:
 It is the method introduced in the original Stochastic Gradient
Boosting article
 It is the method used in many successful real world studies
 We have found it to be more accurate than the other methods
◦ Many decisions that affect many people are made using a TreeNet model
◦ Major new fraud detection engine uses TreeNet
◦ David Cossock of Yahoo recently published a paper on uses of TreeNet in
web search
 TreeNet is a fully developed methodology. New capabilities
include:
◦ Graphical display of the impact of any predictor
◦ New automated ways to test for existence of interactions
◦ New ways to identify and rank interactions
◦ Ability to constrain model: allow some interactions and disallow others.
◦ Method to recast TreeNet model as a logistic regression.

79.  Built on CART trees and thus
◦ Immune to outliers
◦ Selects variables
◦ Results invariant with monotone transformations of variables
◦ Handles missing values automatically
 Resistant to mislabeled target data
◦ In medicine cases are commonly misdiagnosed
◦ In business, occasionally non-responders flagged as “responders”
 Resistant to overtraining- generalizes very well
 Can be remarkably accurate with little effort
 Trains very rapidly; comparable to CART

80.  2007 PAKDD competition: home loans up-sell to credit card owners
2nd place
◦ Model built in half a day using previous year submission as a blueprint
 2006 PAKDD competition: customer type discrimination 3rd place
◦ Model built in one day. 1st place accuracy 81.9% TreeNet accuracy 81.2%
 2005 BI-CUP Sponsored by University of Chile attracted 60 competitors
 2004 KDDCup “Most Accurate”
 2003 “Duke University/NCR Teradata CRN modeling competition
◦ Most Accurate and Best Top Decile Lift on both in and out of time samples
 A major financial services company has tested TreeNet across a
broad range of targeted marketing and risk models for the past two
years
◦ TreeNet consistently outperforms previous best models (around 10%
AUROC)
◦ TreeNet models can be built in a fraction of the time previously devoted
◦ TreeNet reveals previously undetected predictive power in data

81.  Begin with one very small tree as initial model
◦ Could be as small as ONE split generating 2 terminal nodes
◦ Typical model will have 3-5 splits in a tree, generating 4-6 terminal nodes
◦ Output is a continuous response surface regardless of the target type
 Hence, Probability modeling type for classification
◦ Model is intentionally “weak”- shrink all model predictions towards zero
by multiplying all predictions by a small positive learn rate
 Compute “residuals” for this simple model (prediction error) for
every record in data
◦ The actual definition of the residual in this case is driven by the type of the
loss function
 Grow second small tree to predict the residuals from first tree
 Continue adding more and more trees until a reasonable amount
has been added
◦ It is important to monitor accuracy on an independent test sample

82.  (insert chart)

83.  Trees are kept small (2-6 nodes common)
 Updates are small- can be as small as .01,.001,.0001
 Use random subsets of the training data in each cycle
◦ Never train on all the training data in any one cycle
 Highly problematic cases are IGNORED
◦ If model prediction starts to diverge substantially from observed data, that
data will not be used in further updates
 TN allows very flexible control over interactions:
◦ Strictly Additive Models (no interactions allowed)
◦ Low level interactions allowed
◦ High level interactions allowed
◦ Constraints: only specific interactions allowed (TN PRO)

84.  As TN models consist of hundreds or even thousands of trees there is no
useful way to represent the model via a display of one or two trees
 However, the model can be summarized in a variety of ways
◦ Partial Dependency Plots: These exhibit the relationship between the
target and any predictor- as captured by the model
◦ Variable Importance Rankings: These stable rankings give an excellent
assessment of the relative importance of predictors
◦ ROC and Gains Curves: TN Models produce scores that are typically unique
for each scored record
◦ Confusion Matrix: Using an adjustable score threshold this matrix displays
the model false positive and false negative rates
 TreeNet models based on 2-node trees by definition EXCLUDE interactions
◦ Model may be highly nonlinear but is by definition strictly additive
◦ Every term in the model is based on a single variable (single split)
 Build TreeNet on a larger tree (default is 6 nodes)
◦ Permits up to 5-way interaction but in practice is more like 3-way interaction
 Can conduct informal likelihood ratio test TN(2-node) versus TN(6-
node)
 Large differences signal important interactions

85.  (insert graphs)
 The results of running TN on the Boston
Housing Database are shown
 All of the key insights agree with previous
findings by MARS and CART

86.  Slope reverses due to interaction
 Note that the dominant pattern is downward
sloping, but that a key segment defined by
the 3rd variable is upward sloping
 (insert graph)

88.  CART: Model is one optimized Tree
◦ Model is easy to interpret as rules
 Can be useful for data exploration, prior to attempting a more complex
model
◦ Model can be applied quickly with a variety of workers:
 A series of questions for phone bank operators to detect fraudulent
purchases
 Rapid triage in hospital emergency rooms
◦ In some cases may produce the best or the most predictive model, for example
in classification with a barely detectable signal
◦ Missing values handled easily and naturally. Can be deployed effectively even
when new data have a different missingness pattern
 Random Forests: combination of many LARGE trees
◦ Unique nonparametric distance metric that works in high dimensional spaces
◦ Often predicts well when other models work poorly, e.g. data with high level
interactions
◦ In the most difficult data sets can be the best way to identify important
variables
 Tree Net: combination of MANY small trees
◦ Best overall forecast performance in many cases
◦ Constrained models can be used to test the complexity of the data structure
non-parametrically
◦ Exceptionally good with binary targets

89.  Neural Networks, combination of a few sigmoidal activation
functions
◦ Very complex models can be represented in a very compact form
◦ Can accurately forecast both levels and slopes and even higher order
derivatives
◦ Can efficiently use vector dependent variables
 Cross equation constraints can be imposed. (see Symmetry constraints for
feedforward network models of gradient systems, Cardell, Joerding, and
Li, IEEE Transactions on Neural Networks, 1993)
◦ During deployment phase, forecasts can be computed very quickly
 High voltage transmission lines use a neural network to detect whether there
has been a lightning strike and are fast enough to shut down the line before
it can be damaged
 Kernel function estimators, use a local mean or a local regression
◦ Local estimates easy to understand and interpret
◦ Local regression versions can estimate slopes and levels
◦ Initial estimation can be quick

90.  Random Forests:
◦ Models are large, complex and un-interpretable
◦ Limited to moderate sample sizes (usually less than 100,000
observations)
◦ Hard to tell in advance which case Random Forests will work well
on
◦ Deployed models require substantial computation
 Tree Net
◦ Models are large and complex, interpretation requires additional
work
◦ Deployed models either require substantial computation or post-
processing of the original model into a more compact form
 CART
◦ In most cases models are less accurate than TreeNet
◦ Works poorly in cases where effects are approximately linear in
continuous variables or additive over many variables

91.  Neural Networks:
◦ Neural Networks cover such a wide variety of models that no good widely-
applicable modeling software exists or may even be possible
 The most dramatic successes have been with Neural Network models that are
idiosyncratic to the specific case, and ere developed with great effort
 Fully optimized Neural Network parameter estimates can be very difficult to
compute, and sometimes perform substantially worse than initial statistically
inferior estimates. (this is called the “over training” issue)
◦ In almost all cases initial estimation is very compute intensive
◦ Limited to very small numbers of variables (typically between about 6 and
20 depending on the application)
 Kernel Function Estimators:
◦ Deployed models can require substantial computation
◦ Limited to small numbers of variables
◦ Sensitive to distance measures. Even a modest number of variables can
degrade performance substantially, due to the influence of relatively
unimportant variables on the distance metric

92.  Breiman, L., J. Friedman, R. Olshen and C. Stone
(1984), Classification and Regression Trees, Pacific Grove:
Wadsworth
 Breiman, L. (1996). Bagging predictors. Machine
Learning, 24, 123-140.
 Hastie, T., Tibshirani, R., and Friedman, J.H (2000). The
Elements of Statistical Learning. Springer.
 Freund, Y. & Schapire, R. E. (1996). Experiments with a
new boosting algorithm. In L. Saitta, ed., Machine
Learning: Proceedings of the Thirteenth National
Conference, Morgan Kaufmann, pp. 148-156.
 Friedman, J.H. (1999). Stochastic gradient boosting.
Stanford: Statistics Department, Stanford University.
 Friedman, J.H. (1999). Greedy function approximation: a
gradient boosting machine. Stanford: Statistics
Department, Stanford University.