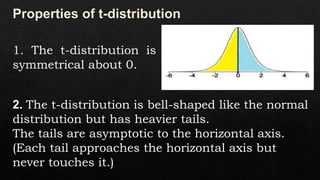
The document discusses the t-distribution, which is used as an alternative to the normal distribution when sample sizes are small and/or the population variance is unknown. The t-distribution was developed by William Sealy Gosset using the pseudonym "Student" and accounts for uncertainty in population parameters by having heavier tails than the normal distribution. Key properties of the t-distribution include being symmetrical around 0, bell-shaped, and having tails that are asymptotic to the horizontal axis. The degree of freedom affects the shape, with lower freedom resulting in a lower peak and thicker tails.

2. When we know the standard deviation of the population,
we can compute a z-score and use the normal
distribution to evaluate probabilities.
But sample sizes are sometimes small, and often we do
not know the standard deviation of the population.
When either of these problems occurs, the solution is to
use a different distribution.

3. It is probability distribution that is used to estimate
population parameters when the sample size is small (𝑖. 𝑒.
𝑠𝑎𝑚𝑝𝑙𝑒 𝑠𝑖𝑧𝑒 < 30) and/or when the population variance is
unknown.
It was developed by William Sealy Gosset in 1908. He used the
pseudonym or pen name “Student” when he published his paper
which describes the distribution. That is why it is called
“Student’s t-distribution”.
In the problem he analyzed, the sample size might be as low as
three.

5. 1. The t-distribution is
symmetrical about 0.
2. The t-distribution is bell-shaped like the normal
distribution but has heavier tails.
The tails are asymptotic to the horizontal axis.
(Each tail approaches the horizontal axis but
never touches it.)

7. The total area under a t-distribution curve is 1 or 100%.
One can say that the area under the t-distribution curve
represents the probability, or the percentage associated
with specific sets of t-values.

8. The lesser the degree of freedom, the lower is its
peak and the thicker is its tails. As the degree of
freedom increases, the tails become flatter, and the
peak becomes higher.