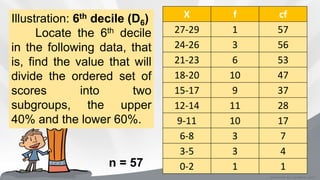
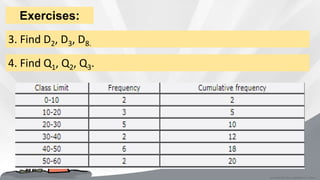
This document defines and provides formulas and examples for calculating quartiles and deciles from both ungrouped and grouped data. Quartiles and deciles are statistical measures used to divide a data set into four and ten equal parts, respectively. The document explains that quartiles are calculated as Q1, Q2, Q3 to divide the data into the lower 25%, middle 50%, and upper 25%. Deciles are calculated as D1-D9 to divide the data into ten equal parts. Modified formulas are provided to calculate quartiles and deciles from grouped frequency distribution data. Examples are included to demonstrate calculating these measures.

1. Point
Measures
Prepared by:
Sweet Charey Lou T. Mapindan

2. Point Measures
Quartiles
Deciles

3. Deciles
Deciles are nine partitional values of the data or
the given set of observation into ten equal parts.
These 9 values are represented by D₁, D₂, D₃, D₄,
D₅, D₆, D₇, D₈ and D₉ .
They shows the 10%, 20%, 30%, 40%, 50%, 60%, 70%,
80% and 90%

4. Deciles for Ungrouped Data
D1 = value of
(𝒏+𝟏)
𝟏𝟎
𝒕𝒉 𝒊𝒕𝒆𝒎
D2 = value of
𝟐(𝒏+𝟏)
𝟏𝟎
𝒕𝒉 𝒊𝒕𝒆𝒎
D9 = value of
𝟗(𝒏+𝟏)
𝟏𝟎
𝒕𝒉 𝒊𝒕𝒆𝒎
Formula:

5. Deciles for Ungrouped Data
Solution:
First, arrange the scores in ascending
order.
Example:
Find the 7th Decile or D7 of the following test scores
of a random sample of 10 students.
36 43 41 29 16 24 34 21 19 29

6. Ascending order:
16 19 21 24 29 29 34 36 41 43
Formula:
D7 = value of
𝟕(𝒏+𝟏)
𝟏𝟎
𝒕𝒉 𝒊𝒕𝒆𝒎 D7 = ?
D7 =
𝟕(𝟏𝟎+𝟏)
𝟏𝟎
=
7(11)
10
=
77
10
= 7.7 = 8
D7 is the 8th element
Therefore, D7 = 36

7. Deciles for Grouped Data
Those values of the distribution that divided total
frequency to ten groups.
Md = P50 = D5 = Q2

8. Md = P50 = D5 = Q2
Md = LL (
𝒏
𝟐
− 𝒇 𝒃
𝒇 𝒘
)𝒊
LL is the real lower limit of the median class,
𝒏 is the total number of cases in the distribution,
𝒇 𝒃 is the number of cases below the median class,
𝒇 𝒘 is the number of cases within the median class, and
𝒊 is the size of class interval (𝒊 = number of scores in a
class or group)

9. Illustration: 6th decile (D6)
Locate the 6th decile
in the following data, that
is, find the value that will
divide the ordered set of
scores into two
subgroups, the upper
40% and the lower 60%.
X f cf
27-29 1 57
24-26 3 56
21-23 6 53
18-20 10 47
15-17 9 37
12-14 11 28
9-11 10 17
6-8 3 7
3-5 3 4
0-2 1 1n = 57

10. To estimate D6, the modified formula would be
D6 = 𝑳𝑳 𝑫 𝟔
+(
𝟔𝒏
𝟏𝟎
−𝒇 𝒃
𝒇 𝒘
)𝒊
𝑳𝑳 𝑫 𝟔
is the real lower limit of the D6 class,
𝒏 is the total number of cases in the distribution,
𝒇 𝒃 is the number of cases below the D6 class,
𝒇 𝒘 is the number of cases within the D6 class, and
𝒊 is the size of class interval (𝒊 = number of scores in
a class or group)

11. D6 is
𝟔𝒏
𝟏𝟎
= (0.6)(57) = 34.2
From the cf column, the 34.2nd case falls in the interval
(15-17), thus, the D6 class is the interval (15-17), and
𝑳𝑳 𝑫 𝟔
= 𝟏𝟒. 𝟓
𝒇 𝒃 = 28
𝒇 𝒘 = 9
𝒊 = 3

12. Using the modified formula:
D6 = 𝑳𝑳 𝑫 𝟔
+(
𝟔𝒏
𝟏𝟎
−𝒇 𝒃
𝒇 𝒘
)𝒊
𝐷6 = 14.5 +
34.2 − 28
9
3
𝐷6 = 14.5 +
6.2
9
3
= 14.5+2.06667
𝐷6= 16.57
This means that students
with scores greater than
16.57 belong to the upper
40% of the class and
students with scores less
than 16.57 belong to the
lower 60% of the class.

13. Quartiles
Quartiles are the score points which divide a
distribution into four equal parts.
25% 50% 75% 100%
Lower
Quartile
Middle
Quartile
Upper
Quartile
Q1 Q2 Q3

14. Quartiles for Ungrouped Data
Formula:

15. Example:
Following is the data of marks obtained by 20 students
in a test of statistics. Find Quartiles Q1 Q2 Q3 :
53 74 82 42 39 20 81 68 58 28
67 54 93 70 30 55 36 37 29 61
20 28 29 30 36 37 39 42 53 54
55 58 61 67 68 70 74 81 82 93
Ascending ordern = 20

16. Quartiles for Grouped Data
Illustration: 3rd quartile
(Q3)
Locate the 3rd quartile
(Q3) in the following data,
that is, find the value that
will divide the ordered set
of scores into two
subgroups, the upper 25%
and the lower 75%.
X f cf
27-29 1 57
24-26 3 56
21-23 6 53
18-20 10 47
15-17 9 37
12-14 11 28
9-11 10 17
6-8 3 7
3-5 3 4
0-2 1 1
n = 57

17. To estimate Q3, the modified formula would be
Q3 = 𝑳𝑳Q3
+(
𝟑𝒏
𝟒
−𝒇 𝒃
𝒇 𝒘
)𝒊
𝑳𝑳 𝑸 𝟑
is the real lower limit of the Q3 class,
𝒏 is the total number of cases in the distribution,
𝒇 𝒃 is the number of cases below the Q3 class,
𝒇 𝒘 is the number of cases within the Q3 class, and
𝒊 is the size of class interval (𝒊 = number of scores in
a class or group)

18. The position of Q3 is
3𝑛
4
= (0.75) (57) = 42.75
From the cf column, the 42.75th case falls in the
interval (18-20), thus, the Q3 class is the interval (18-
20), and
𝑳𝑳 𝑸 𝟑
= 𝟏𝟕. 𝟓
𝒇 𝒃 = 37
𝒇 𝒘 = 10
𝒊 = 3

19. 𝑄3 = 17.5 +
42.75 − 37
10
3
𝑄3 = 14.5 +
5.75
10
3
= 17.5+1.725
𝑄3= 19.225
Using the modified formula:
Q3 = 𝑳𝑳Q3
+(
𝟑𝒏
𝟒
−𝒇 𝒃
𝒇 𝒘
)𝒊
This means that students
with scores greater than
19.225 belong to the
upper 25% of the class
and students with scores
less than 19.225 belong to
the lower 75% of the
class.

20. Exercises:
1. Find the 1st quartile, 2nd quartile, and third quartile,
given the scores of 10 students in their Mathematics
quiz.
38 43 56 55 25 27 25 39 40 45
2. Find the 6th decile, 7th decile, and 9th decile, given
the scores of 10 students in their Mathematics quiz.

21. Exercises:
3. Find D2, D3, D8.
4. Find Q1, Q2, Q3.

22. Thank you for listening!
God bless. 