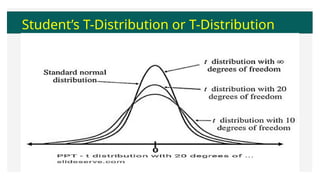
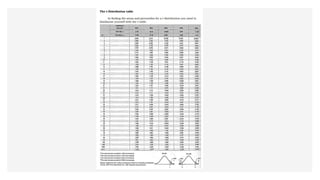
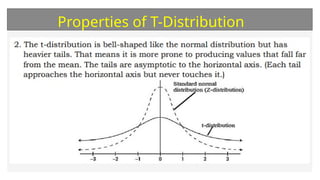
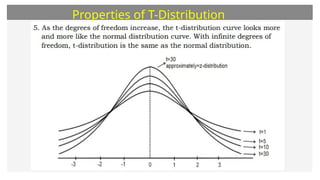
This document discusses the student's t-distribution, highlighting its properties, such as its application for small sample sizes and unknown population standard deviations. It explains the concept of degrees of freedom, which affects the distribution's shape and variance, and emphasizes that the means of t-distribution characteristics are zero with a variance greater than one. Additionally, it includes true/false assessments and sample problems related to the t-distribution and degrees of freedom.

2. STUDENT’S
T-DISTRIBUTION
LESSON 7

3. LESSON OBJECTIVES
illustrates a T-Distribution and its
properties;
1
2
3
identifies Percentiles using T-Distribution
table;

4. Student’s T-Distribution or T-Distribution

5. Student’s T-Distribution or T-Distribution
The Student’s t-distribution is a
probability distribution that is used to
estimate population parameters when
the sample size is small ( . .
𝑖 𝑒 𝑠𝑎𝑚𝑝𝑙𝑒
is less than 30) and/or when the
𝑠𝑖𝑧𝑒
population standard deviation is
unknown.

6. Student’s T-Distribution or T-Distribution
The z-distribution and t-distribution
are almost identical except for
different standard deviations used in
the formula in converting sample
mean scores to z-scores and t-scores.

7. Student’s T-Distribution or T-Distribution

8. Student’s T-Distribution or T-Distribution
The major difference between z-distribution and t-
distribution is that each t-distribution is
distinguished by its degrees of freedom. Degrees
of freedom are defined as the number of
"observations“ in the data that are free to vary
when estimating statistical parameters. In
situations where you have one population and
your sample size is n, the degrees of freedom (df)
is calculated using the formula, df = n-1

9. EXAMPLE
The number of degrees of freedom is
one less than the sample size.
So, if the sample size (n) is 25, the
number of degrees of freedom is 24.
Also, at t-distribution having 16
degrees of freedom, the sample size is
17.

10. Student’s T-Distribution or T-Distribution
These degrees of freedom change how
the probability distribution looks. The
exact shape of the t-distribution depends
on the degrees of freedom. The
probability distribution of t has more
dispersion than the normal probability
distribution associated with z.

11. Student’s T-Distribution or T-Distribution

13. Properties of T-Distribution

14. Properties of T-Distribution

15. Properties of T-Distribution
3. The mean, median, and mode
of the t-distribution are all equal
to zero.

16. Properties of T-Distribution
4. The variance is always greater than 1. It is
equal to where df is the number of degrees of
freedom. As the number of degrees of
freedom increases and approaches infinity,
the variance approaches 1. Using the formula,
if the number of degrees of freedom is 10, the
variance is

17. Properties of T-Distribution

18. Properties of T-Distribution
6. The standard deviation and
variance of the t-distribution
varies with the sample size. It is
always greater than 1. Unlike the
normal distribution, which has a
standard deviation of 1.

19. Properties of T-Distribution
7. The total area under a t-
distribution curve is 1 or 100%.
The area under the t-distribution
curve represents the probability
or the percentage associated with
specific sets of t-values.

20. LET’S TRY IT! – ½ crosswise
A. True or False
B. Solving

21. 1. The t-distribution is used to estimate population parameters
when the sample size is small and/or the population variance is
unknown.
2. The mean, median and mode are all equal to zero.
3. The variance is equal to 1.
4. The t-distribution curve is bell-shaped.
5. The standard deviation of t-distribution is always greater than
1.
6. Half of the total area under the t-distribution curve is equal to 1.
7. The curve is symmetrical about its zero.
8. The shape of the t-distribution curve depends on the sample
mean.
9. The tails of the t-distribution curve approach the horizontal
axis but never touch it.
10. As the degrees of freedom increase, the t-distribution curve
looks more and more like the normal distribution.

22. Solve the following and show your
solution.
1.Solve the degrees of freedom (df) if the
sample size is 27.
2.Determine the sample size if the
degrees of freedom (df) is 19.
3.If df = 24, n = ?