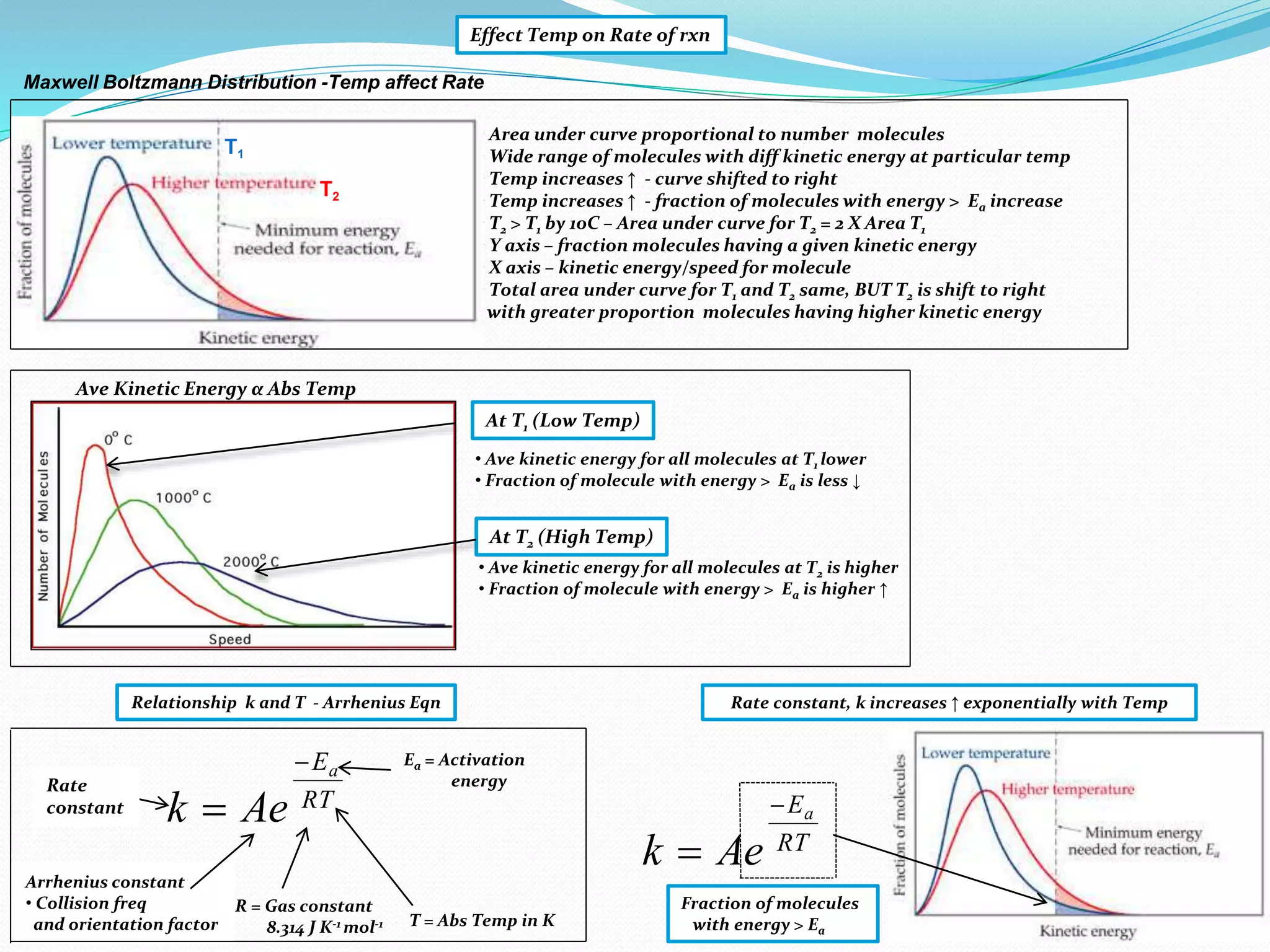
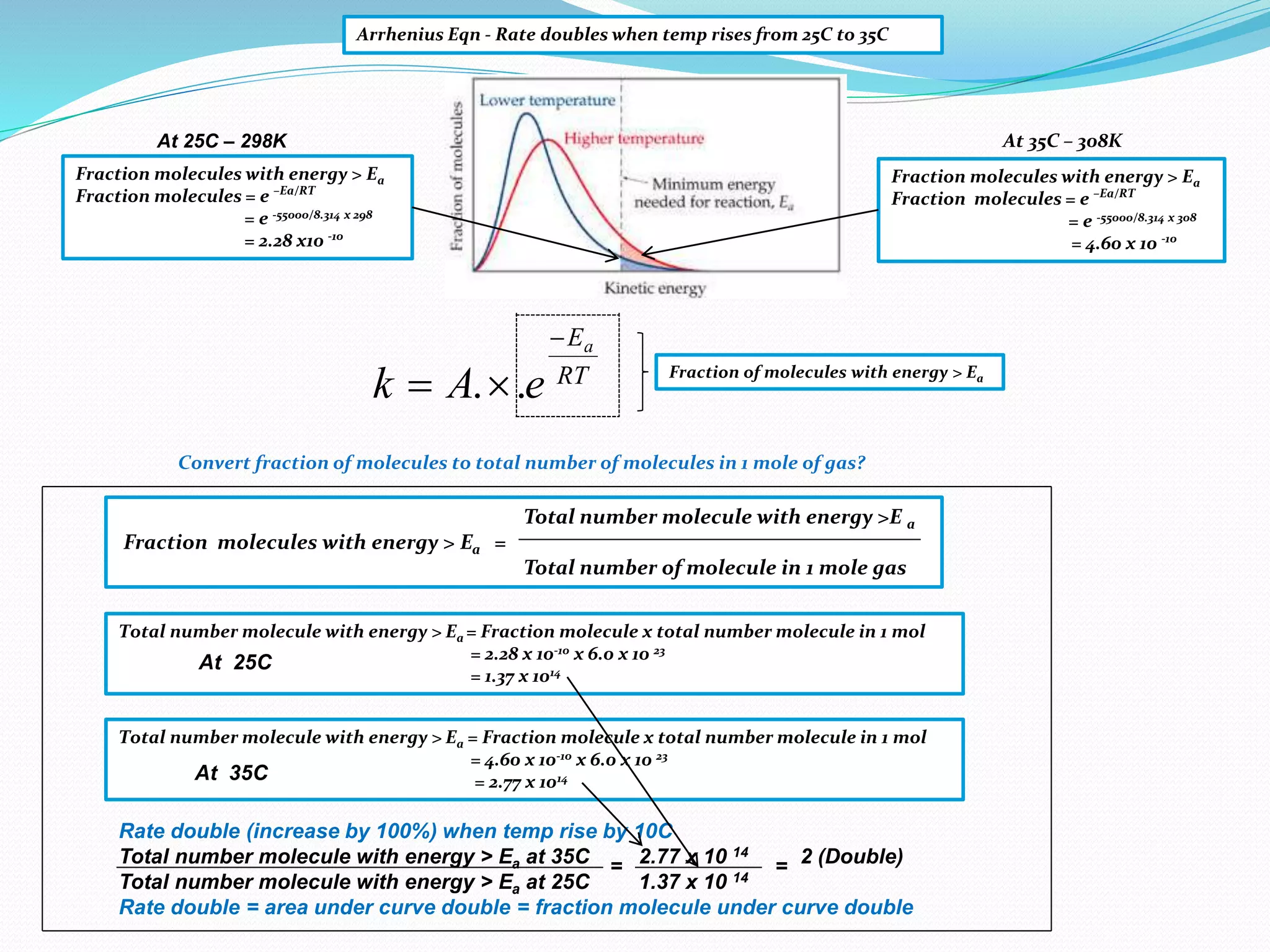
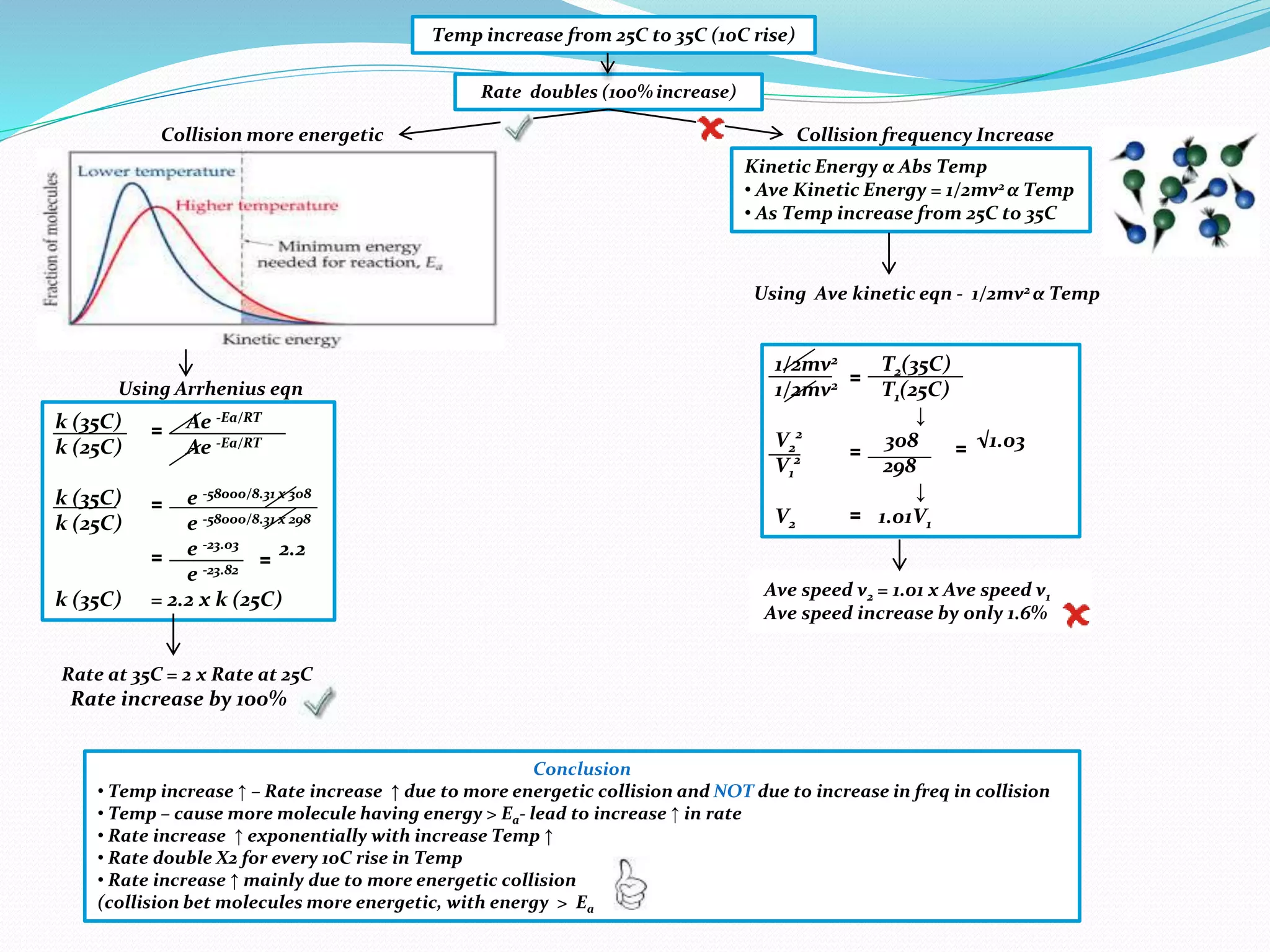
This document provides a tutorial on collision theory, the Arrhenius equation, and the Maxwell-Boltzmann distribution curve. It explains that for a chemical reaction to occur, molecules must collide with the correct orientation and with energy greater than the activation energy. It also discusses how increasing the temperature or concentration of reactants increases the rate of reaction by increasing the frequency and energy of collisions. The Arrhenius equation quantitatively describes the relationship between reaction rate and temperature. The Maxwell-Boltzmann distribution curve illustrates how more molecules have energy above the activation energy at higher temperatures, explaining the temperature dependence of reaction rates.

1. http://lawrencekok.blogspot.com
Prepared by
Lawrence Kok
Tutorial on Collision Theory, Arrhenius Equation
Maxwell Boltzmann Distribution Curve.

2. Collision Theory
Chemical rxn to occur bet A +B
• Molecule collide with right orientation (geometry)
( effective collision take place)
• Molecule collide with total energy greater > activation energy
• Effective collision will lead to product formation
Collision bet A + B
No product formation
• Energy collision < activation energy
• Collision not in correct orientation
or energetic enough to overcome Ea
Product formation
• Energy collision > activation energy
• Collision energetic enough to overcome Ea
Rate of Reaction
• Conc reactant increase ↑
• Freq of collision increase ↑
• Freq of effective collision increase ↑
• Temp increase ↑ by 10 C
• Rate increase ↑ by 100%
• Exponential relationship
bet Temp and Rate
Rate = k [A]1[B]1 1st order – A
1st order – B
Conc A doubles x2 – Rate x2
Conc A triples x3 – Rate x3
Collision Theory
• Temp increase ↑ by 10C
• Fraction of molecules with
energy > Ea doubles
• Rate increases ↑ by 100%
Ineffective collision Effective collision
Concentration
Temperaturedepends

3. Effect Temp on Rate of rxn
• Area under curve proportional to number molecules
• Wide range of molecules with diff kinetic energy at particular temp
• Temp increases ↑ - curve shifted to right
• Temp increases ↑ - fraction of molecules with energy > Ea increase
• T2 > T1 by 10C – Area under curve for T2 = 2 X Area T1
• Y axis – fraction molecules having a given kinetic energy
• X axis – kinetic energy/speed for molecule
• Total area under curve for T1 and T2 same, BUT T2 is shift to right
with greater proportion molecules having higher kinetic energy
Ave Kinetic Energy α Abs Temp
• Ave kinetic energy for all molecules at T1 lower
• Fraction of molecule with energy > Ea is less ↓
• Ave kinetic energy for all molecules at T2 is higher
• Fraction of molecule with energy > Ea is higher ↑
Maxwell Boltzmann Distribution -Temp affect Rate
At T1 (Low Temp)
At T2 (High Temp)
T1
T2
RT
Ea
Aek


Relationship k and T - Arrhenius Eqn
Rate
constant
Arrhenius constant
• Collision freq
and orientation factor
Ea = Activation
energy
T = Abs Temp in K
R = Gas constant
8.314 J K-1 mol-1
RT
Ea
Aek


Fraction of molecules
with energy > Ea
Rate constant, k increases ↑ exponentially with Temp

4. Fraction molecules with energy > Ea
Fraction molecules = e –Ea/RT
= e -55000/8.314 x 298
= 2.28 x10 -10
Fraction molecules with energy > Ea
Fraction molecules = e –Ea/RT
= e -55000/8.314 x 308
= 4.60 x 10 -10
Total number molecule with energy > Ea = Fraction molecule x total number molecule in 1 mol
= 2.28 x 10-10 x 6.0 x 10 23
= 1.37 x 1014
Total number molecule with energy > Ea = Fraction molecule x total number molecule in 1 mol
= 4.60 x 10-10 x 6.0 x 10 23
= 2.77 x 1014
Total number molecule with energy >E a
Fraction molecules with energy > Ea =
Total number of molecule in 1 mole gas
Rate double (increase by 100%) when temp rise by 10C
Total number molecule with energy > Ea at 35C 2.77 x 10 14 2 (Double)
Total number molecule with energy > Ea at 25C 1.37 x 10 14
Rate double = area under curve double = fraction molecule under curve double
Arrhenius Eqn - Rate doubles when temp rises from 25C to 35C
At 35C – 308KAt 25C – 298K
Convert fraction of molecules to total number of molecules in 1 mole of gas?
At 35C
At 25C
= =
Fraction of molecules with energy > EaRT
Ea
eAk

 ..

5. Temp increase from 25C to 35C (10C rise)
Rate doubles (100% increase)
Collision more energetic
Kinetic Energy α Abs Temp
• Ave Kinetic Energy = 1/2mv2 α Temp
• As Temp increase from 25C to 35C
1/2mv2 T2(35C)
1/2mv2 T1(25C)
↓
V2
2
308 √1.03
V1
2
298
↓
V2 1.01V1
Ave speed v2 = 1.01 x Ave speed v1
Ave speed increase by only 1.6%
Using Arrhenius eqn
k (35C) Ae -Ea/RT
k (25C) Ae -Ea/RT
k (35C) e -58000/8.31 x 308
k (25C) e -58000/8.31 x 298
e -23.03 2.2
e -23.82
k (35C) = 2.2 x k (25C)
Rate at 35C = 2 x Rate at 25C
Rate increase by 100%
Collision frequency Increase
Using Ave kinetic eqn - 1/2mv2 α Temp
=
=
=
=
=
= =
=
Conclusion
• Temp increase ↑ – Rate increase ↑ due to more energetic collision and NOT due to increase in freq in collision
• Temp – cause more molecule having energy > Ea- lead to increase ↑ in rate
• Rate increase ↑ exponentially with increase Temp ↑
• Rate double X2 for every 10C rise in Temp
• Rate increase ↑ mainly due to more energetic collision
(collision bet molecules more energetic, with energy > Ea

6. Temp and rate constant link by Arrhenius Eqn
X + Y → Z
Rate of rxn = (Total number collision) x ( fraction collision, energy >Ea) x ( [X] [Y] )
Arrhenius Constant
A
Fraction molecule energy > Ea
e –Ea/RT
Conc
[X][Y]
Rate of rxn = A e –Ea/RT [X][Y]
Rate of rxn = k [X] [Y]
If conc constant BUT Temp changes, combine eqn 1 and 2
Rate of rxn = k [X]1
[Y]1
= A e –Ea/RT [X][Y]
k = A e –Ea/RT
Rate rxn written in TWO forms
Rate of rxn = A e –Ea/RT [X] [Y]
Eqn 1 Eqn 2
Cancel both sides
Rate of rxn = A e –Ea/RT [X][Y]
Fraction molecule energy > Ea
e –Ea/RT
Conc
[X][Y]
Temp increase
Fraction with energy > Ea increase
Rate increase exponentially
Conc increase
Freq collision increase
Rate increase
Arrhenius Eqn - Ea by graphical Method
RT
Ea
eAk

 ..







TR
E
Ak a 1
lnln 






TR
E
Ak a 1
303.2
lglg
Plot ln k vs 1/T
• Gradient = -Ea/R
• ln A = intercept y axis
Plot log k vs 1/T
• Gradient = -Ea/R
• log A = intercept y axis
ln both sides log both sides
ln k lg k
1/T1/T
-Ea/R -Ea/R

7. Decomposition of 2HI ↔ H2 + I2 at diff temp and k was measured. Find Ea
Arrhenius Eqn
Ea from its gradient
Arrhenius Eqn - Ea by graphical Method
Temp/K 1/T k/dm3 mol-1 s-1 ln k
633 1.58 x 10-3 1.78 x 10-5 -10.94
666 1.50 x 10-3 1.07 x 10-4 -9.14
697 1.43 x 10-3 5.01 x 10-4 -7.60
715 1.40 x 10-3 1.05 x 10-5 -6.86
781 1.28 x 10-3 1.51 x 10-2 -4.19
1
RT
Ea
eAk

 .. 






TR
E
Ak a 1
lnln
Plot ln k vs 1/T
2
ln both sides
-Ea/R
Gradient = -Ea/R
Gradient = -2.25 x 104
-2.25 x 104 = -Ea/R
Ea = 2.25 x 104 x 8.314
= 1.87 x105 Jmol-1
ln k
1/T
Rxn 2HI ↔ H2 + I2 Find Ea
1
1 lnln
RT
E
Ak a

2
2 lnln
RT
E
Ak a

12
4
3
121
2
1066.1
600
1
650
1
314.8107.2
105.3
ln
11
ln






























kJmolE
E
TTR
E
k
k
a
a
a












121
2 11
ln
TTR
E
k
k a
600K ---k = 2.7 x 10-14 650K --- k= 3.5 x 10-3

8. Decomposition of Mass X at diff temp and k was measured. Find Ea
Arrhenius Eqn - Ea by graphical Method
3
1
1 lnln
RT
E
Ak a

2
2 lnln
RT
E
Ak a

1
121
2
7.52
273
1
286
1
314.855.0
4.1
ln
11
ln


























kJmolE
E
TTR
E
k
k
a
a
a












121
2 11
ln
TTR
E
k
k a
Time/m Mass left/g Mass loss
0 130 0
20 120 10
60 98 32
80 86 44
273K ---k = 0.55 286K ---k = 1.4
Time/m Mass left/g Mass loss
0 130 0
10 115 15
15 106 24
30 86 44
Plot mass loss vs time
Gradient will give rate constant, k
Mass loss
273K 286K
Mass loss
time
time
Gradient
↓
rate constant, k = 0.55
Gradient
↓
rate constant, k = 1.4

9. Acknowledgements
Thanks to source of pictures and video used in this presentation
Thanks to Creative Commons for excellent contribution on licenses
http://creativecommons.org/licenses/
Prepared by Lawrence Kok
Check out more video tutorials from my site and hope you enjoy this tutorial
http://lawrencekok.blogspot.com