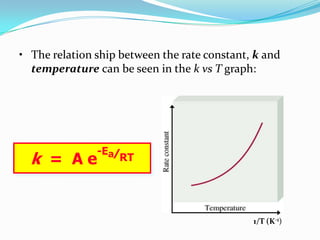
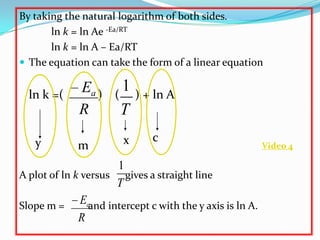
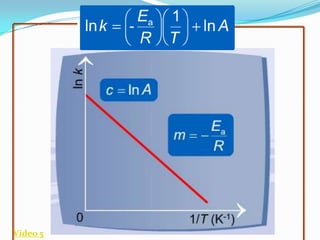
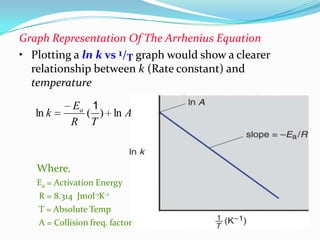
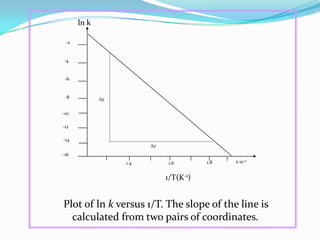
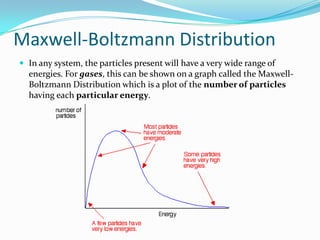
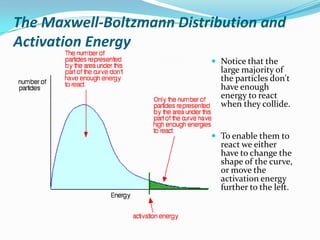
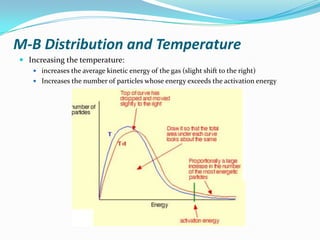
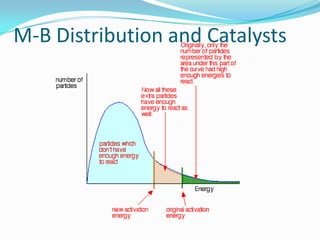
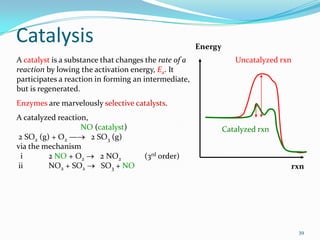
The document discusses reaction kinetics and methods for determining reaction rates. It defines reaction rate and explains how to express reaction rates using concentration changes over time. It also discusses calculating reaction rates from experimental data and determining the rate laws and orders of reactions. Integrated rate laws that relate concentration to time for first-order reactions are also covered, including calculating rate constants and half-lives. The Arrhenius equation, which relates reaction rate to temperature, is introduced.

1. CHEMISTRY II
SCI 4211
Prepared by Hartini Hamzah
1

2. REACTION KINETICS
2

3. Reaction Rate Defined
Reaction rate: changes in a concentration of a
product or a reactant per unit time.
[]
Reaction rate = ——
t
concentration
[]
change
[]
t
t
3

4. Expressing reaction rates
For a chemical reaction, there are many ways to express the reaction rate. The
relationships among expressions depend on the equation.
Note the expression and reasons for their relations for the reaction
2 NO + O2 (g) = 2 NO2 (g)
[O2]
1
[NO]
1
[NO2]
Reaction rate = – ——— = – — ———— = — ———
t
2
t
2
t
Make sure you can write expressions for any reaction and figure out the
relationships. For example, give the reaction rate expressions for
2 N2O5 = 4 NO2 + O2
How can the rate expression be unique and universal?
4

5. Calculating reaction rate
The concentrations of N2O5 are 1.24e-2 and 0.93e-2 M at 600 and 1200 s after
the reactants are mixed at the appropriate temperature. Evaluate the reaction
rates for
2 N2O5 = 4 NO2 + O2
Solution:
(0.93 – 1.24)e-2
– 0.31e-2 M
Decomposition rate of N2O5 = – ———————— = – ——————
1200 – 600
600 s
= 5.2e-6 M s-1.
Note however,
rate of formation of NO2 = 1.02e-5 M s-1.
rate of formation of O2 = 2.6e-6 M s-1.
Be able to do this type
problems
The reaction rates
are expressed in 3
forms
5

6. Determine Reaction Rates
To measure reaction rate, we measure the concentration of either a
reactant or product at several time intervals.
The concentrations are measured using spectroscopic method or
pressure (for a gas). For example, the total pressure increases for
the reaction:
2 N2O5 (g)
4 NO2 (g) + O2(g)
Because 5 moles of gas products are produced from 2 moles of gas
reactants. For the reaction
CaCO3 (s)
barometer
CaO(s) + CO2 (g)
The increase in gas pressure is entirely due to CO2 formed.
6

7. Rate Laws
 An equation that relates the rxn rate and the
concentration of reactants
Rate Determining Step
Slow
Rate = k[HBr][O2]

8. Rate Laws
 If no mechanism is given, then…
2H2 + 2NO  N2 + 2H2O
Rate = k[H2]2[NO]2

9. Rate Orders
 0, 1st and 2nd order rates
 Order is dependent upon what will yield a straight
line
1st order
ln [reactants]
[reactants]
0 order
1/[reactants]
2nd order

10. Rate Orders
 1st order: reaction rate is directly proportional to the
concentration of that reactant
 2nd order: reaction rate is directly proportional to the
square of that reactant
 0 order: rate is not dependant on the concentration of
that reactant, as long as it is present.
For Individual Components:

11. Rate Orders
 Overall reaction orders is equal to the sum of the
reactant orders.
 Always determined experimentally!
For Overall Order:

12. Calculating for k
A + 2B  C
Rate = k[A][B]2
Experiment
Initial [A]
Initial [B]
Rate of
Formation of
C
1
0.20 M
0.20 M
2.0 x 10-4
M/min
2
0.20 M
0.40 M
8.0 x 10-4
M/min
3
0.40 M
0.40 M
1.6 x 10-3
M/min
What is the value of k, the rate
constant?

13. Calculating for k
Experiment
Initial [A]
Initial [B]
Rate of
Formation
of C
1
0.20 M
0.20 M
2.0 x 10-4
M/min
2
0.20 M
0.40 M
8.0 x 10-4
M/min
3
0.40 M
0.40 M
1.6 x 10-3
M/min
Rate = k[A][B]2
2.0 x 10-4 = k[0.20][0.20]2
2.0 x 10-4 = k(0.008)
k = 2.50 x 10-2 min-1 M-2

14. Practice
1. In a study of the following reaction:
2Mn2O7(aq) → 4Mn(s) + 7O2(g)
When the manganese heptoxide concentration was changed from 7.5 x
10-5 M to 1.5 x 10-4 M, the rate increased from 1.2 x 10-4 to 4.8 x 10-4. Write
the rate law for the reaction.
Rate = k[Mn2O7]2
2. For the reaction:
A+B→C
When the initial concentration of A was doubled from 0.100 M to 0.200
M, the rate changed from 4.0 x 10-5 to 16.0 x 10-5. Write the rate law &
determine the rate constant for this reaction.
Rate = k[A]2
Constant = 4.0 x 10-3 M/s

15. More Practice
New Rate = 8.1 x 10-5 M/s
3. The following reaction is first order:
CH3NC(g) → CH3CN(g)
The rate of this reaction is 1.3 x 10-4 M/s when the reactant
concentration is 0.040 M. Predict the rate when [CH3NC] = 0.025.
4. The following reaction is first order:
(CH2)3(g) → CH2CHCH3 (g)
What change in reaction rate would you expect if the pressure of
the reactant is doubled?
An increase by a factor of 2

16. Integrated Rate Laws
concentrations as functions of time
One reactant A decomposes in 1st or 2nd order rate law.
Differential rate law
Integrated rate law
– d[A] / dt = k
[A] = [A]o – k t
d[A]
– —— = k [A]
dt
[A] = [A]o e – k t or ln [A] = ln [A]o – k t
d[A]
– —— = k [A]2
dt
1
1
—— – —— = k t
[A]
[A]o
[A] conc at t
[A]o conc at t = 0
Describe, derive and apply the integrated rate laws
Learn the strategy to determine rate-law
16

17. Concentration and time of 1st order reaction
Describe the features of plot of [A] vs. t and ln[A] vs. t for 1st order reactions.
Apply the technique to evaluate k or [A] at various times.
[A]
ln[A
]
ln [A] = ln [A]o – k t
[A] = [A]o e – k t
t½
t
t
17

18. Half life & k of First Order Decomposition
The time required for half of A to decompose is called half life t1/2.
Since
[A] = [A]o e – k t
When
t = t1/2, [A] = ½ [A]o
Thus
ln ½ [A]o = ln [A]o – k t1/2
or
ln [A] = ln [A]o – k t
– ln 2 = – k t1/2
k t1/2 = ln 2 = 0.693
relationship between k and t1/2
Radioactive decay usually follow 1st order kinetics, and half life of an isotope is
used to indicate its stability.
Evaluate t½ from k or k from t½
18

19. st
1
order reaction calculation
N2O5 decomposes according to 1st order kinetics, and 10% of it decomposed in 30
s. Estimate k, t½ and percent decomposed in 500 s.
Solution next
19

20. st
1
order reaction calculation
N2O5 decomposes according to 1st order kinetics, and 10% of it decomposed in 30 s.
Estimate k, t½ and percent decomposed in 500 s.
Solution: Assume [A]o = [N2O5]o = 1.0, then [A] = 0.9 at t = 30 s or
0.9 = 1.0 e – k t
apply [A] = [A]o e– k t
ln 0.9 = ln 1.0 – k 30 s
– 0.1054 = 0 – k * 30
k = 0.00351 s – 1
t½ = 0.693 / k = 197 s apply k t ½ = ln 2
[A] = 1.0 e – 0.00351*500 = 0.173
Percent decomposed: 1.0 – 0.173 = 0.827 or 82.7 %
After 2 t½ (2*197=394 s), [A] = (½)2 =¼, 75% decomposed.
After 3 t½ (3*197=591 s), [A] = (½)3 =1/8, 87.5% decomposed.
Apply integrated rate law to solve problems
20

21. Molecularity of Elementary Reactions
The total order of rate law in an elementary reaction is molecularity.
The rate law of elementary reaction is derived from the equation. The order is the
number of reacting molecules because they must collide to react.
A molecule decomposes by itself is a unimolecular reaction (step);
two molecules collide and react is a bimolecular reaction (step); &
three molecules collide and react is a termolecular reaction (step).
O3
O2 + O
rate = k [O3]
NO2 + NO2
NO3 + NO
rate = k [NO2]2
Br + Br + Ar
Br2 + Ar*
rate = k [Br]2[Ar]
Caution: Derive rate laws this way only for elementary reactions.
21

22. The Arrhenius Equation
 The dependence of the rate constant of a reaction on
temperature can be expressed by the following equation
known as Arrhenius equation.
k=A e
Ea
RT
Ea = activation energy
k = rate constant
R = gas constant
T = absolute temperature
e = the base of the natural
logarithm scale
A = quantity represents the collision
frequency (frequency factor)

23. • The relation ship between the rate constant, k and
temperature can be seen in the k vs T graph:
-Ea∕
k = Ae
RT
1/T (K-1)

24. By taking the natural logarithm of both sides.
ln k = ln Ae -Ea/RT
ln k = ln A – Ea/RT
 The equation can take the form of a linear equation
ln k =(
y
Ea ) ( 1 ) + ln A
R
T
m
x
c
1
A plot of ln k versus gives a straight line
T
Slope m = Eaand intercept c with the y axis is ln A.
R
Video 4

25. Video 5

26. Graph Representation Of The Arrhenius Equation
• Plotting a ln k vs 1/T graph would show a clearer
relationship between k (Rate constant) and
temperature
ln k
Ea 1
( ) ln A
R T
Where,
Ea = Activation Energy
R = 8.314 Jmol-1K-1
T = Absolute Temp
A = Collision freq. factor

27. Example 1
The rate constants for decomposition of acetaldehyde
2HI(g)
H2(g) + I2(g)
were measured at five different temperatures.The data
are shown below. Plot ln k versus 1/T, and determine
the activation energy (in kJ/mole) for the reaction.
k (1/M s)
T (K)
3.52 x 10-7
283
3.02 x 10-5
356
2.19 x 10-4
393
1.16 x 10-3
427
3.95 x 10-2
508

28. Solution
We need to plot ln k on the y-axis versus 1/T
on the x-axis. From the given data we obtain
ln k
1/T (K-1)
14.860
1.80 x 10-3
10.408
1.59 x 10-3
8.426
1.50 x 10-3
6.759
1.43 x 10-3
3.231
1.28 x 10-3

29. ln k
-2
-4
-6
-8
y
-10
-12
-14
x
-16
1.4
1.6
1.8
x 10-3
1/T(K-1)
Plot of ln k versus 1/T. The slope of the line is
calculated from two pairs of coordinates.

30. Slope =
(-14.0) – (-3.9)
(1.75– 1.3) x 10-3 K-1
= -2.24 x 104 K
 Finally, calculate the activation energy from the slope:
 The slope, m = – Ea/R.
Ea = – R (m)
= (–8.314 J K-1 mol-1) (–2.24 x 104 K)
= 1.9 x 105 J mol-1
= 190 kJ mol-1

31.  An equation relating the rate constants k1 and k2 at
temperatures T1 and T2 can be used to calculate the
activation energy or to find the rate constant at
another temperature if the activation energy is
known.
ln k1 = ln A – Ea/RT1
ln k2 = ln A – Ea/RT2
 Subtracting ln k2 from ln k1 gives
ln k1 – ln k2 = Ea/R (1/T2 – 1/T1)
Video 6

33. Activation Energy
 Collisions only result in a reaction if the particles
collide with enough energy to get the reaction started.
This minimum energy required is called the
activation energy for the reaction.
 Only a fraction of the total population of a chemical
species will be able to collide with enough energy to
react (E ≥ Ea)

34. Maxwell-Boltzmann Distribution
 In any system, the particles present will have a very wide range of
energies. For gases, this can be shown on a graph called the MaxwellBoltzmann Distribution which is a plot of the number of particles
having each particular energy.

35. The Maxwell-Boltzmann Distribution and
Activation Energy
 Notice that the
large majority of
the particles don't
have enough
energy to react
when they collide.
 To enable them to
react we either
have to change the
shape of the curve,
or move the
activation energy
further to the left.

36. M-B Distribution and Temperature
 Increasing the temperature:
 increases the average kinetic energy of the gas (slight shift to the right)
 Increases the number of particles whose energy exceeds the activation energy

37. Catalysts and Activation Energy
 To increase the rate of a reaction you need to increase
the proportion of successful collisions.
 Catalysts increase the rate of reaction by providing an
alternative way for the reaction to happen which has a
lower activation energy.

38. M-B Distribution and Catalysts

39. Catalysis
Energy
A catalyst is a substance that changes the rate of a
reaction by lowing the activation energy, Ea. It
participates a reaction in forming an intermediate,
but is regenerated.
Uncatalyzed rxn
Enzymes are marvelously selective catalysts.
A catalyzed reaction,
NO (catalyst)
2 SO2 (g) + O2 —
2 SO3 (g)
via the mechanism
i
2 NO + O2
2 NO2
ii
NO2 + SO2
SO3 + NO
Catalyzed rxn
(3rd order)
rxn
39

40. Homogenous vs. heterogeneous catalysts
A catalyst in the same phase (gases and solutions) as the reactants is a
homogeneous catalyst. It effective, but recovery is difficult.
When the catalyst is in a different phase than reactants (and products), the process
involve heterogeneous catalysis. Chemisorption, absorption, and adsorption cause
reactions to take place via different pathways.
Platinum is often used to catalyze hydrogenation
Catalytic converters reduce CO and NO emission.
40

41. Enzymes – selective catalysts
Enzymes are a long protein molecules that fold into balls. They often have a
metal coordinated to the O and N sites.
Molecules catalyzed by enzymes are called substrates. They are held by
various sites (together called the active site) of the enzyme molecules and
just before and during the reaction. After having reacted, the products P1 & P2
are released.
Enzyme + Substrate
ES
ES (activated complex)
P1 + P2 + E
Enzymes are biological catalysts for biological systems.
41

42. Summary
 Maxwell-Boltzmann Energy Distribution Curve
 distribution of a population of a chemical by energy
 Used to show effect of temperature and catalysts on the rate of a
chemical reaction
 Temperature
 changes average kinetic energy of population
 shifts and distorts the M-B Distribution curve
 changes the proportion of particles with Ea.
 Catalysts
 provide alternative pathway with a lower the activation energy
 Ea on M-B curve is shifted left
 no effect on distribution curve itself

43. 43