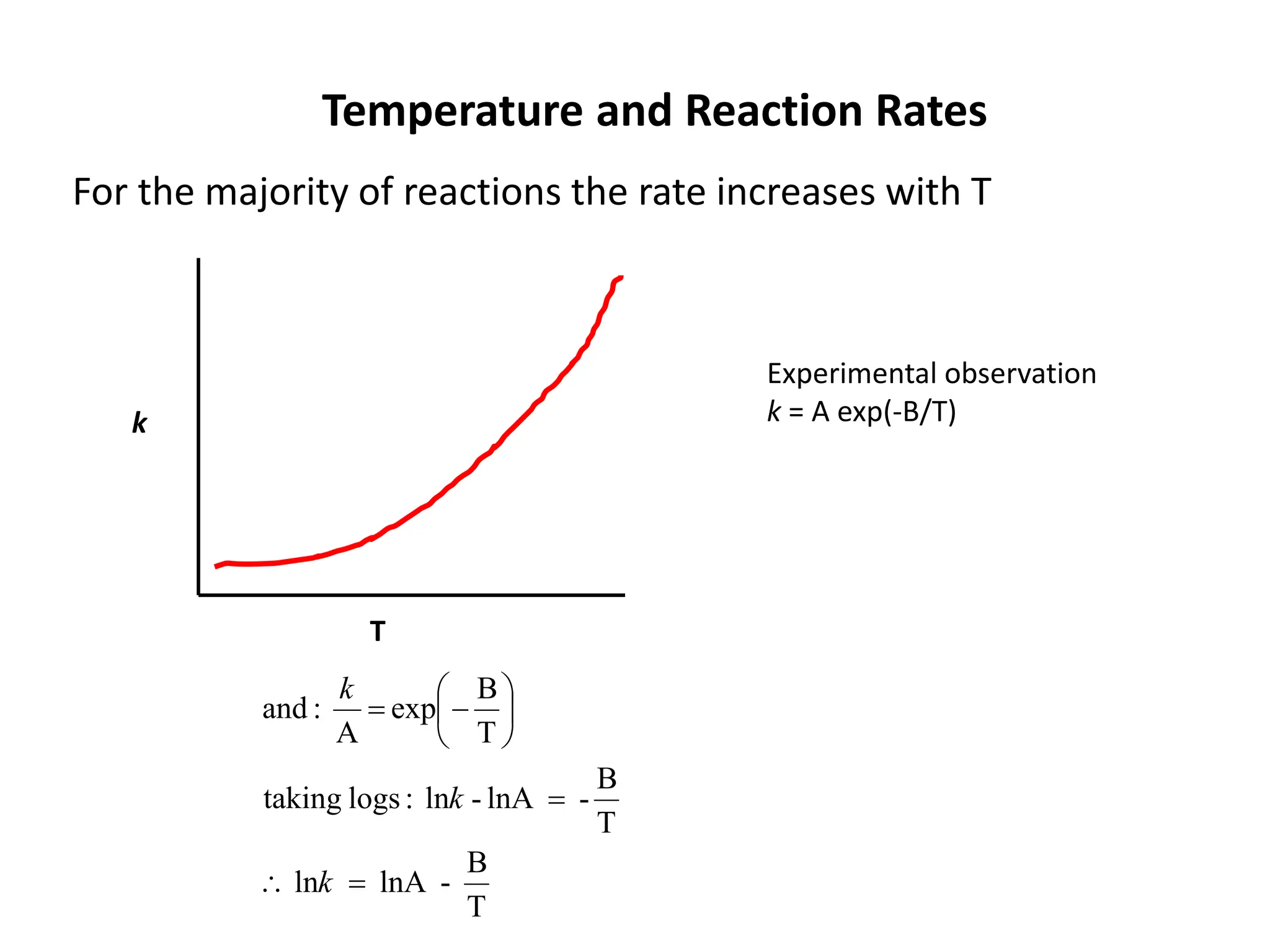
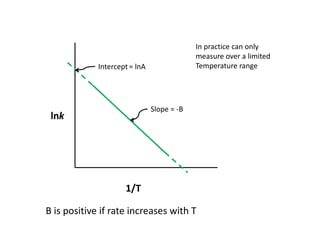
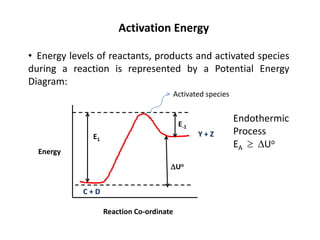
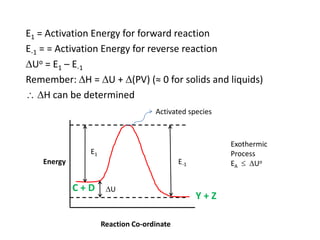
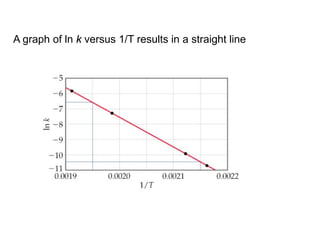
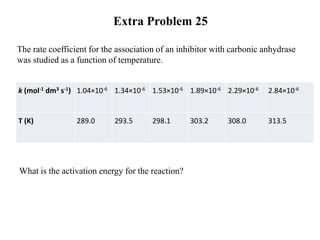
The document discusses the relationship between temperature and reaction rates, referencing the Arrhenius equation and activation energy. It details methods for experimentally determining activation energy and rate coefficients at various temperatures, including graphical methods to analyze data. Examples and problems related to chemical reactions under varying temperatures are also provided to demonstrate these concepts.

1. Temperature and Reaction Rates
For the majority of reactions the rate increases with T
k
T
Experimental observation
k = A exp(-B/T)
T
B
-
lnA
ln
T
B
-
lnA
-
ln
:
logs
taking
T
B
exp
A
:
and
=
∴
=






−
=
k
k
k

2. lnk
1/T
Intercept = lnA
Slope = -B
In practice can only
measure over a limited
Temperature range
B is positive if rate increases with T

3. Van’t Hoff Treatment
• Just as equilibrium constant K varies with T, so does k
Remember?
• Temperature dependence of K is given by:
Consider the following reaction:
C + D Y + Z
2
RT
U
dT
dlnK ο
∆
=
k1
k-1

4. 2
1
-
1
-
2
1
1
2
1
1
1
-
1
1
1
2
1
-
1
1
-
1
1
-
1
1
-
1
RT
E
dT
dln
RT
E
dT
dln
:
equations
2
into
splitting
RT
dT
dln
-
dT
dln
U
RT
U
dT
dln
-
dT
dln
ln
-
ln
ln
lnK
and
K
=
=
−
=
∴
−
=
°
∆
°
∆
=
∴
=
=
=
−
−
k
k
E
E
k
k
E
E
k
k
k
k
k
k
k
k

5. 





=






=






=
=
=
∴
RT
E
-
Aexp
:
Generally
RT
E
-
exp
A
RT
E
-
exp
A
:
gives
g
integratin
dT
RT
E
dln
and
dT
RT
E
dln
1
-
1
-
1
-
1
1
1
2
1
-
1
-
2
1
1
k
k
k
k
k
Thus, the experimentally determined term B is
related to an energy term associated with the reaction

6. Arrhenius Treatment
“Normal molecules exist in equilibrium with activated
molecules: Only activated molecules react”
E is the energy required to form the activated species from
reactants
E = Activation Energy = EA
The Arrhenius Equation 





=
RT
E
-
Aexp A
k

7. Activation Energy
• Energy levels of reactants, products and activated species
during a reaction is represented by a Potential Energy
Diagram:
Energy
Reaction Co-ordinate
E1
E-1
∆Uo
C + D
Y + Z
Endothermic
Process
EA ≥ ∆Uo
Activated species

8. E1 = Activation Energy for forward reaction
E-1 = = Activation Energy for reverse reaction
∆Uo = E1 – E-1
Remember: ∆H = ∆U + ∆(PV) (≈ 0 for solids and liquids)
∴ ∆H can be determined
Energy
Reaction Co-ordinate
Activated species
E1
∆U
C + D
Y + Z
E-1
Exothermic
Process
EA ≤ ∆Uo

9. Determining EA
Only obtained by experiment
Measure k at 2 different temperatures








=








∴








−
=








=
=
2
1
1
2
A
1
2
1
2
A
1
2
2
A
2
2
1
A
1
1
T
T
T
-
T
R
E
ln
T
1
T
1
R
E
-
ln
and
p
higher tem
RT
E
-
lnA
ln
T
lower temp
RT
E
-
lnA
ln
T
k
k
k
k
k
k

10. Consider a reaction with EA = 50 kJmol-1. What is the effect of
increasing T from 300 to 310 K?
rise
ure
K temperat
10
every
for
doubled
is
t
coefficien
Rate
1.91
310
300
300
310
8.314
10
50
ln
1
2
3
1
2
=






×
−
×
=
k
k
k
k

11. In-class Problem 21
The reaction 4A + 3B → 2C +3D is first order in A and second order in B. The
measured rate coefficient is found to be 3.5×10-6 dm6mol-2s-2 at 300 K and
8.5×10-6 dm6mol-2s-2 at 310 K.
Calculate the activation energy.
Determine the rate coefficient at 330 K.

12. In-class Problem 22
The rate coefficient for a reaction at 30°C is measured to be exactly three times
that of the value at 20°C. Calculate the activation energy.

13. Graphical Method for Determination of Activation Energy
The following table shows the rate coefficients for the
rearrangement of methyl isonitrile at various temperatures
(a) From these data, calculate the activation energy for the
reaction.
(b) What is the value of the rate coefficient at 430.0 K?

14. Analyze and Plan: We are given the rate coefficients, k,
measured at several temperatures. We can obtain EA from the
slope of a graph of ln k versus 1/T . Once we know EA we can use
the Arrhenius equation together with the given rate data to
calculate the rate coefficient at 430.0 K.
Solve: (a) We must first convert the temperatures from degrees
Celsius to Kelvin. We then take the inverse of each temperature,
1/T and the natural log of each rate coefficient, ln k. This gives
us the following table:

15. A graph of ln k versus 1/T results in a straight line

16. The slope of the line is obtained by choosing two well-separated
points, as shown, and using the coordinates of each:
Because logarithms have no units, the numerator in this equation is
dimensionless. The denominator has the units of 1/T namely, K-1. Thus, the
overall units for the slope are K. The slope equals –EA/R. We use the value
for the molar gas constant R = 8.314 J/mol K and obtain
Divide by 1000 to convert to kJ

17. (b) To determine the rate coefficient, k1, at T1 = 430 K we can use the
Arrhenius equation with EA = 160 kJ/mol, and one of the rate
coefficients and temperatures from the given data, such as k2 = 2.52 ×
10-5 s-1 and T2 = 462.9K
Thus,
Note that the units of k1 are the same as those of k2

18. In-class Problem 23
The thermal decomposition of ethanol (CH3CHO) is a second order reaction.
Write down an expression for the rate of loss of ethanol in terms or reactant
concentration. The rate coefficients for the reaction at various temperatures were
measured as follows
Use a graphical method to determine the activation energy (in kJ mol-1)
and the pre-exponential factor (in dm3 mol-1 s-1)
T (°C) 427 487 537 637 727
k (dm3 mol-1 s-1) 0.011 0.105 0.178 20.0 145.0

19. In-class Problem 24
The rate coefficients for the gas phase decomposition of ethane at various
temperatures were measured as follows
From the data determine the activation energy for the decomposition
and calculate the pre-exponential factor, A
k (s-1) 2.5×10-5 8.2×10-5 23.1×10-5 57.6×10-5 141.5×10-5
T (K) 823 843 863 883 903

20. The rate coefficient for the association of an inhibitor with carbonic anhydrase
was studied as a function of temperature.
Extra Problem 25
What is the activation energy for the reaction?
k (mol-1 dm3 s-1) 1.04×10-6 1.34×10-6 1.53×10-6 1.89×10-6 2.29×10-6 2.84×10-6
T (K) 289.0 293.5 298.1 303.2 308.0 313.5