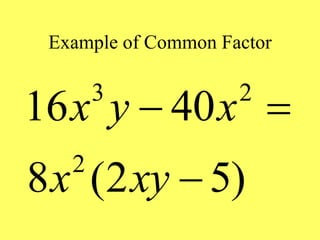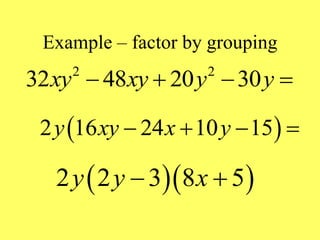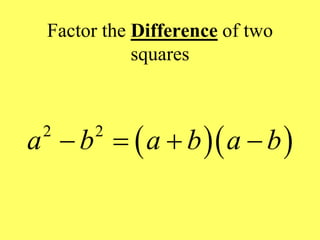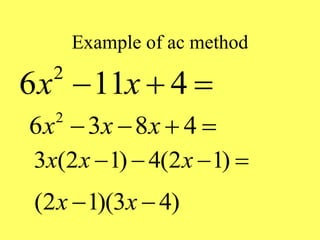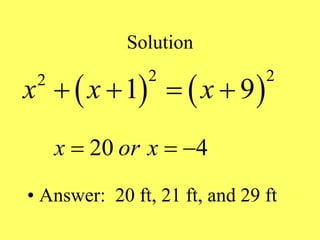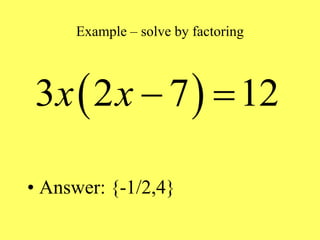(1) The document provides an overview of intermediate algebra topics including exponents, factoring, polynomials, and solving equations. (2) Key concepts discussed include integer exponents, the product rule, factoring common factors, special factoring patterns, and solving polynomial equations by factoring and using the zero-factor property. (3) The goal is to review and reinforce these essential intermediate algebra skills.

1. Intermediate Algebra 098A
Review of
Exponents &
Factoring

2. 1.1 – Integer Exponents
• For any real number b and any natural
number n, the nth power of b is found by
multiplying b as a factor n times.
n
b b b b b
    

3. Exponential Expression – an
expression that involves
exponents
• Base – the number being multiplied
• Exponent – the number of factors of the
base.

4. Product Rule
n n m n
a a a 


5. Quotient Rule
m
m n
n
a
a
a



6. Integer Exponent
1
n
n
a
a



7. Zero as an exponent
0
1 0
a a R
   

8. Calculator Key
• Exponent Key
^

9. Sample problem
3 0
2 5
8
24
x y
x y


5
5
3
y
x


10. more exponents
• Power to a Power
 
n
m mn
a a


11. Product to a Power
 
r r r
ab a b


12. Polynomials - Review
•Addition
•and
•Subtraction

13. Objective:
•Determine the
coefficient and degree
of a monomial

14. Def: Monomial
• An expression that is a constant
or a product of a constant and
variables that are raised to
whole –number powers.
• Ex: 4x 1.6 2xyz

15. Definitions:
• Coefficient: The numerical
factor in a monomial
• Degree of a Monomial: The
sum of the exponents of all
variables in the monomial.

16. Examples – identify the degree
4
8x

4 5
0.5x y

4
5

17. Def: Polynomial:
•A monomial or an
expression that can be
written as a sum or
monomials.

18. Def: Polynomial in one variable:
•A polynomial in which
every variable term has
the same variable.

19. Definitions:
• Binomial: A polynomial
containing two terms.
• Trinomial: A
polynomial containing
three terms.

20. Degree of a Polynomial
•The greatest degree of
any of the terms in the
polynomial.

21. Examples:
6 3 2
2
2
5 3 4 3 2
5 10 9 1
3 4 5
16
3 2 6
x x x x
x x
x
x x y xy y
   
 

   

22. Objective
•Add
•and
•Subtract
•Polynomials

23. To add or subtract Polynomials
• Combine Like Terms
• May be done with columns or
horizontally
• When subtracting- change the
sign and add

24. Evaluate Polynomial Functions
• Use functional notation to
give a polynomial a name
such as p or q and use
functional notation such as
p(x)
• Can use Calculator

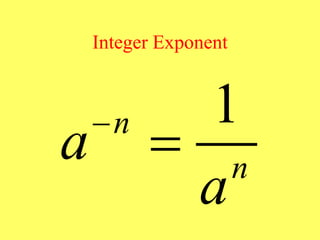
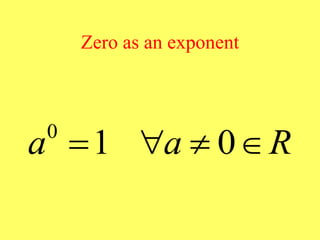
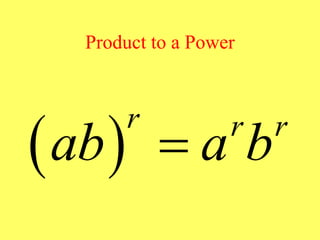
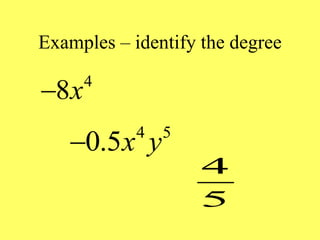
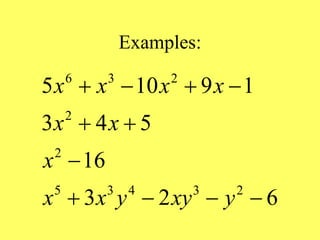
25. Calculator Methods
• 1. Plug In
• 2. Use [Table]
• 3. Use program EVALUATE
• 4. Use [STO->]
• 5. Use [VARS] [Y=]
• 6. Use graph- [CAL][Value]

26. Objective:
•Apply evaluation of
polynomials to real-life
applications.

27. Intermediate Algebra 5.4
•Multiplication
•and
•Special Products

28. Objective
•Multiply
•a
• polynomial
•by a
•monomial

29. Procedure: Multiply a
polynomial by a monomial
• Use the distributive property to
multiply each term in the
polynomial by the monomial.
• Helpful to multiply the
coefficients first, then the
variables in alphabetical order.

30. Law of Exponents
r s r s
b b b 


31. Objectives:
•Multiply Polynomials
•Multiply Binomials.
•Multiply Special
Products.

32. Procedure: Multiplying
Polynomials
• 1. Multiply every term in the
first polynomial by every term
in the second polynomial.
• 2. Combine like terms.
• 3. Can be done horizontally or
vertically.

33. Multiplying Binomials
•FOIL
• First
• Outer
• Inner
• Last

34. Product of the sum and difference
of the same two terms
Also called multiplying
conjugates
   2 2
a b a b a b
   

35. Squaring a Binomial
 
 
2 2 2
2 2 2
2
2
a b a ab b
a b a ab b
   
   
 
2 2
( )
a b a ab b
  

36. Objective:
• Simplify Expressions
• Use techniques as part of a
larger simplification
problem.

37. Albert Einstein-
Physicist
•“In the middle of
difficulty lies
opportunity.”

38. Intermediate Algebra –098A
•Common Factors
•and
•Grouping

39. Def: Factored Form
•A number or
expression written as a
product of factors.

40. Greatest Common Factor (GCF)
• Of two numbers a and b is the
largest integer that is a factor of
both a and b.

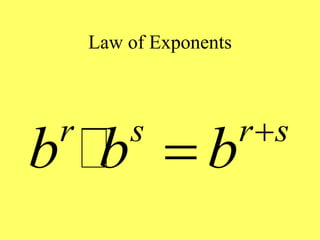
41. Calculator and gcd
• [MATH][NUM]gcd(
• Can do two numbers – input
with commas and ).
• Example: gcd(36,48)=12

42. Greatest Common Factor (GCF)
of a set of terms
•Always do this
FIRST!

43. Procedure: Determine greatest common
factor GCF of 2 or more monomials
• 1. Determine GCF of numerical
coefficients.
• 2. Determine the smallest
exponent of each exponential
factor whose base is common to
the monomials. Write base with
that exponent.
• 3. Product of 1 and 2 is GCF

44. Factoring Common Factor
• 1. Find the GCF of the terms
• 2. Factor each term with the
GCF as one factor.
• 3. Apply distributive property
to factor the polynomial

45. Example of Common Factor
3 2
2
16 40
8 (2 5)
x y x
x xy
 


46. Factoring when first terms is
negative
• Prefer the first term inside parentheses to be
positive. Factor out the negative of the
GCF.
3
2
20 36
4 (5 9)
xy y
y xy
  
 

47. Factoring when GCF is a
polynomial
( 5) ( 5)
( 5)( )
a c b c
c a b
   
 

48. Factoring by Grouping – 4 terms
• 1. Check for a common factor
• 2. Group the terms so each group has a
common factor.
• 3. Factor out the GCF in each group.
• 4. Factor out the common binomial factor –
if none , rearrange polynomial
• 5. Check

49. Example – factor by grouping
2 2
32 48 20 30
xy xy y y
   
 
2 16 24 10 15
y xy x y
   
  
2 2 3 8 5
y y x
 

50. Ralph Waldo Emerson – U.S.
essayist, poet, philosopher
•“We live in
succession , in
division, in parts, in
particles.”

51. Intermediate Algebra 098A
•Special Factoring

52. Objectives:Factor
• a difference of squares
• a perfect square trinomial
• a sum of cubes
• a difference of cubes

53. Factor the Difference of two
squares
  
2 2
a b a b a b
   

54. Special Note
• The sum of two squares is
prime and cannot be factored.
2 2
a b
is prime


55. Factoring Perfect Square
Trinomials
 
 
2
2 2
2
2 2
2
2
a ab b a b
a ab b a b
   
   

56. Factor: Sum and Difference of
cubes
 
 
3 3 2 2
3 3 2 2
( )
( )
a b a b a ab b
a b a b a ab b
    
    

57. Note
• The following is not factorable
2 2
a ab b
 

58. Factoring sum of Cubes -
informal
• (first + second)
• (first squared minus first times
second plus second squared)

59. Intermediate Algebra 098A
• Factoring Trinomials
• of
• General Quadratic
2
ax bx c
 

60. Objectives:
• Factor trinomials of the form
50 15
y y
  
2
2
x bx c
ax bx c
 
 

61. Factoring
• 1. Find two numbers with a product equal
to c and a sum equal to b.
• The factored trinomial will have the form(x
+ ___ ) (x + ___ )
• Where the second terms are the numbers
found in step 1.
• Factors could be combinations of positive
or negative
2
x bx c
 

62. Factoring
Trial and Error
• 1. Look for a common factor
• 2. Determine a pair of coefficients of first
terms whose product is a
• 3. Determine a pair of last terms whose
product is c
• 4. Verify that the sum of factors yields b
• 5. Check with FOIL Redo
2
ax bx c
 

63. Factoring ac method
• 1. Determine common factor if any
• 2. Find two factors of ac whose sum is b
• 3. Write a 4-term polynomial in which by
is written as the sum of two like terms
whose coefficients are two factors
determined.
• 4. Factor by grouping.
2
ax bx c
 

64. Example of ac method
2
6 11 4
x x
  
2
6 3 8 4
x x x
   
3 (2 1) 4(2 1)
x x x
   
(2 1)(3 4)
x x
 

65. Example of ac method
2 2
5 (8 10 3)
y y y
  
 
2 2
5 8 2 12 3
y y y y
   
   
2
5 2 4 1 3 4 1
y y y y
   
 
 
  
2
5 4 1 2 3
y y y
 

66. Factoring - overview
• 1. Common Factor
• 2. 4 terms – factor by grouping
• 3. 3 terms – possible perfect square
• 4. 2 terms –difference of squares
• Sum of cubes
• Difference of cubes
• Check each term to see if completely
factored

67. Isiah Thomas:
• “I’ve always believed no
matter how many shots I
miss, I’m going to make
the next one.”

68. Intermediate Algebra 098A
•Solving Equations
•by
•Factoring

69. Zero-Factor Theorem
•If a and b are real
numbers
•and ab =0
•Then a = 0 or b = 0

70. Example of zero factor property
  
   
5 2 0
5 0 2 0
5 2
5,2 2, 5
x x
x or x
x or x
or
  
   
  
 

71. Solving a polynomial equation by
factoring.
1. Factor the polynomial
completely.
2. Set each factor equal to 0
3. Solve each of resulting equations
4. Check solutions in original
equation.
5. Write the equation in standard
form.

72. Example – solve by factoring
2
3 11 4
x x
 
2
3 11 4 0
x x
  
  
3 1 4 0
x x
  
3 1 0 4 0
x or x
   
1
4
3
x or x

 

73. Example: solve by factoring
 
  
 
3 2
3 2
2
4 12
4 12 0
4 12 0
6 2 0
0,6, 2
x x x
x x x
x x x
x x x
 
  
  
  


74. Example: solve by factoring
• A right triangle has a
hypotenuse 9 ft longer than the
base and another side 1 foot
longer than the base. How long
are the sides?
• Hint: Draw a picture
• Use the Pythagorean theorem

75. Solution
• Answer: 20 ft, 21 ft, and 29 ft
   
2 2
2
1 9
x x x
   
20 4
x or x
  

76. Example – solve by factoring
• Answer: {-1/2,4}
 
3 2 7 12
x x  

77. Example: solve by factoring
• Answer: {-5/2,2}
   
2 2
1 1 1
3 2
2 12 3
x x x
   

78. Example: solve by factoring
• Answer: {0,4/3}
   
2
9 1 4 6 1 3
y y y y y
   

79. Example: solve by factoring
• Answer: {-3,-2,2}
 
3 2
3 13 7 3 1
t t t t
    

80. Sugar Ray Robinson
• “I’ve always believed that
you can think positive just
as well as you can think
negative.”

82. Maya Angelou - poet
• “Since time is the one
immaterial object which we
cannot influence – neither
speed up nor slow down, add
to nor diminish – it is an
imponderably valuable gift.”