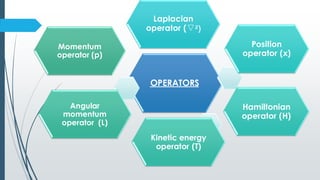
The document outlines fundamental postulates of quantum mechanics, beginning with the significance of the wave function (ψ) as a key property describing a system's state. It details properties of ψ, conditions for eigenfunctions, and the relationship between classical observables and quantum mechanical operators, including the process of obtaining eigenvalues. Additionally, it discusses the derivation of the time-independent Schrödinger wave equation using these postulates to connect classical energy expressions to quantum mechanics.

1. QUANTUM CHEMISTRY
PRINSHILA GANDHI
BSC. CHEMISTRY
POSTULATES

2. POSTULATES OF QUANTUM
MECHANICS

3. POSTULATE #1
Wave function or state
function is an important
property in quantum
mechanics. To every state in
physical system , there is a
function ψ, which defines the
state of system .

4. WAVE FUNCTION (ψ)

5. wave function = quantity that describes wave
characteristics of a particle .
OR
in simple words, it is the storehouse of all
information of a system.
•it is the amplitude with mathematical
importance.
•ψ(r,t) depends on (r) & (t).

6. PROBABLITY DENSITY(ψ²)
probability of finding the particle located at
distance (r) & time (t).
• it is preferable because in quantum mechanics,
there is imaginary value (ⅰ) ,
so by taking square , (i) =vanishes out & it will give
us a real value.
•therefore, ψ² is mostly preferred.

7. Stationary
waves

8. Time dependent wave function

9. POSTULATE #2
The function ψ must be single
valued, finite , smoothly varying
& continuous.
 also, it should follow the
conditions of S, C, F, B, N
(properties of an eigen function).

10. .
S (single
valued)
C
(continuous)
F (finite
value)
B (boundary
conditions)
N
(normalised)

11. POSTULATE #3
For every observable of a
system In classical mechanics,
(like-position, velocity,
momentum ,energy) there
corresponds a mathematical
operator in quantum mechanics.

12. .

13. OPERATORS
Laplacian
operator (▽²)
Position
operator (x)
Hamiltonian
operator (H)
Kinetic energy
operator (T)
Angular
momentum
operator (L)
Momentum
operator (p)

14. HERMITIAN OPERATOR
∫ψ*φ dx =0

16. Postulate IV and Postulate V will
tell us about how we will
calculate the properties of the
system in quantum mechanics…….

17. Postulate IV:
For any measurement of the observable
property associated with the operator Â, the
only value that will ever be observed is the
eigen value ‘a’ which can be obtained from
eigen value equation, i.e.,
Âψ = aψ

18. Explanation of Postulate IV:
• This means that when the operator  acts on the wavefunction ψ,
which is supposed to be suitable for this operator, gives back the
function ψ multiplied by a constant quantity a.
• For the given state, known as the eigenstate of the system, ψ is the
eigenfunction for the operator  and a is the corresponding
eigenvalue.

19. Postulate V:
When ψ is not an eigen value of Â, then we talk
of average values in quantum mechanics.
Explanation of Postulate IV:
• It means that if ψ is an eigen function of Â, then Âψ = aψ. But ψ is
not always an eigen function of Â.
• The expected average value (or expectation value) of an observable
property of a system whose state function is ψ, is given by mean
value theorem:

20. • If ψ is an eigen value of Â, expectation value <a> = a (eigen value).

21. Derivation of time independent
Schrödinger wave equation on
the basis of postulates of
quantum mechanics

22. Let us consider an electron in an atom of mass ‘m’ and it is moving with
velocity ‘v’.
Total energy (E) is the sum of kinetic energy (T) and potential energy (V).
E = T+V ---(1)
---(2)
p = total momentum of the particle
Put equation (2) in (1):
---(3)

23. Classical expression E has to be converted to its correspondingquantum
mechanical operator for energy. The following replacements are required:
V is potential energy. So it is a function of position co-ordinates.Hence
operator is V itself.
Hamiltonian operator is the operator for energy.
Now,

24. ---(3)
Here,
According to 4th postulate of quantum mechanics we know that Âψ = aψ.
So we must have Ĥψ = Eψ. ---(4)
Put equation (3) in (4):
It is the time independentSchrodingerwave equation.