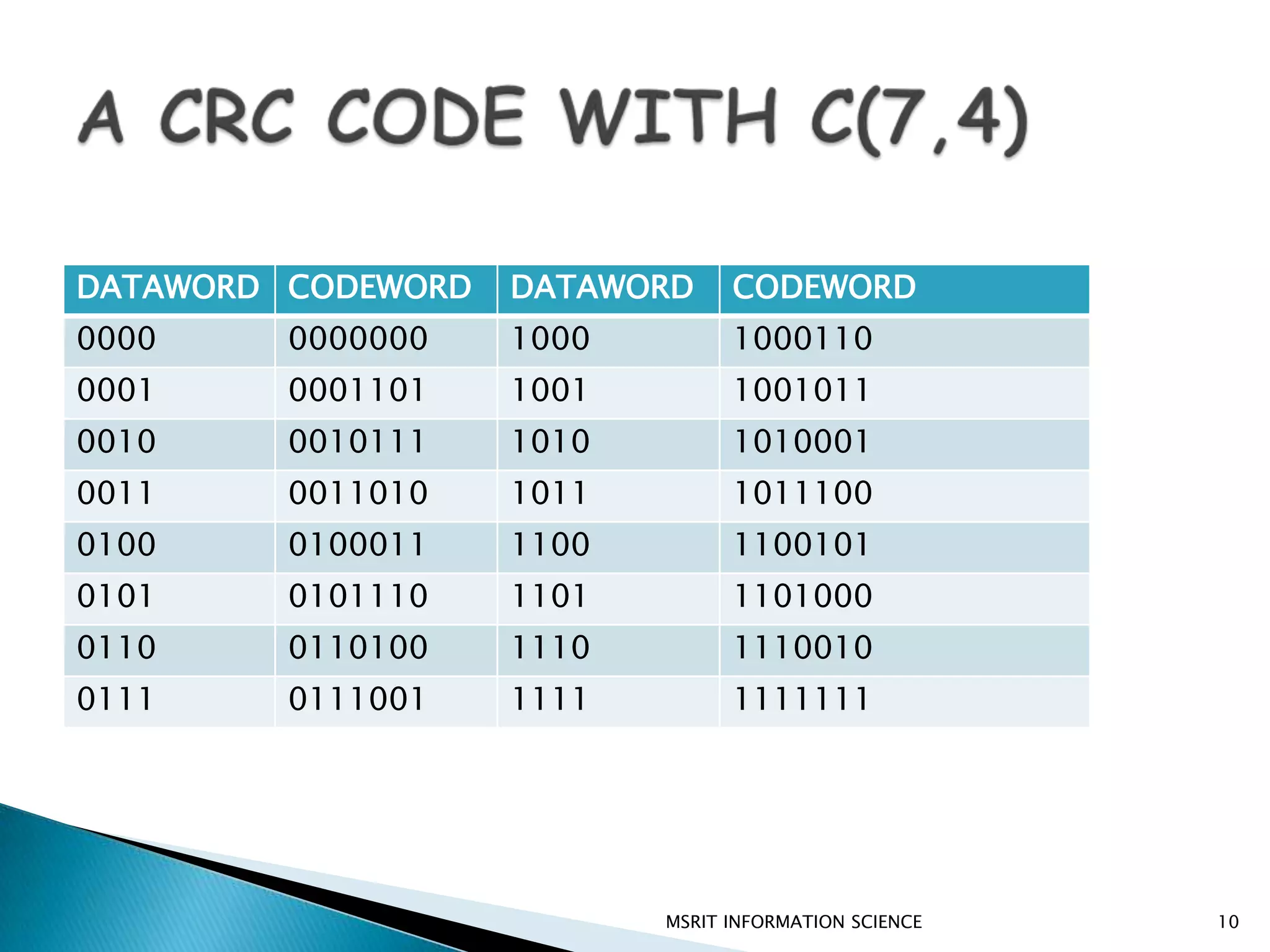
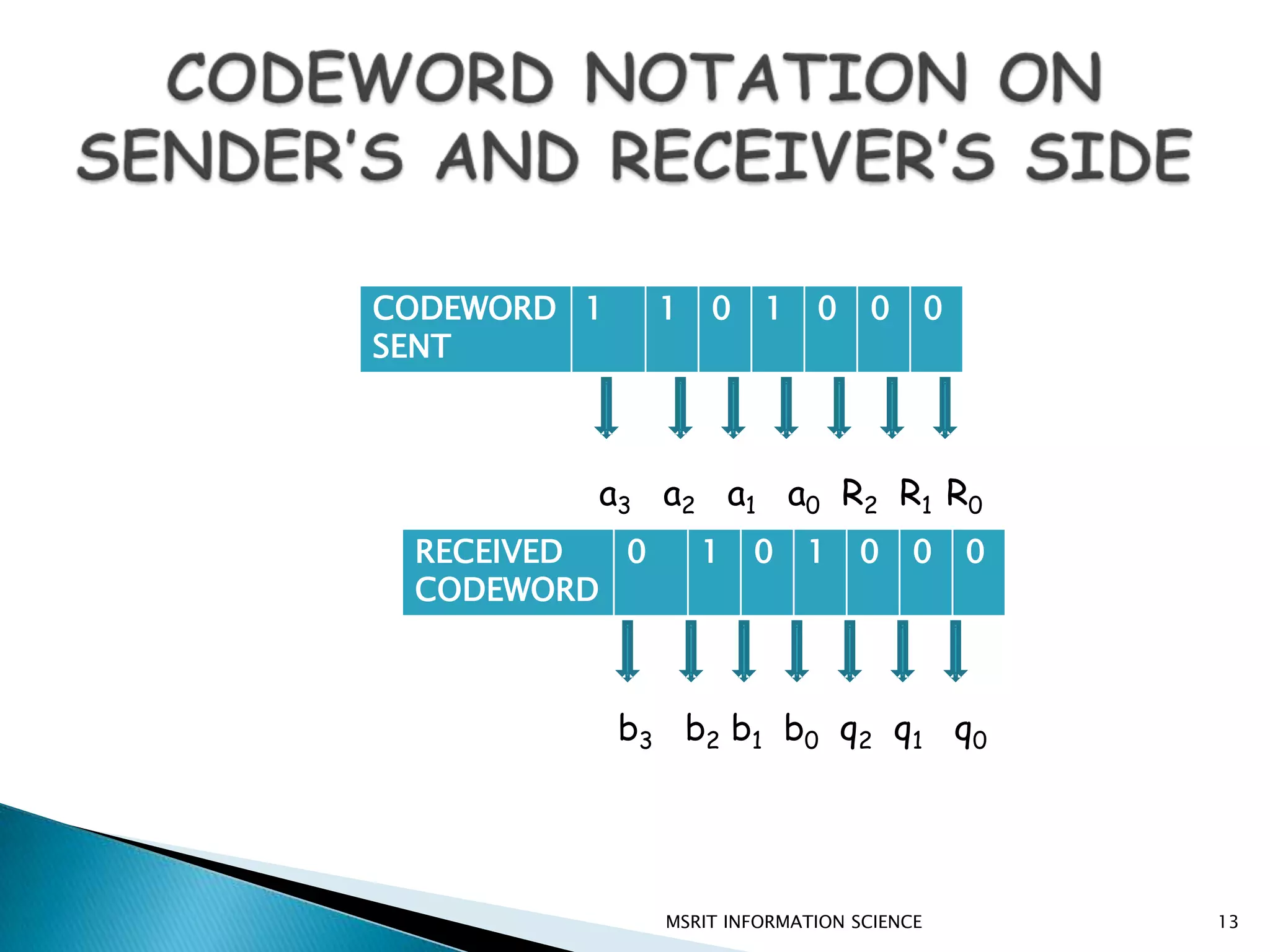
This document discusses error detection and correction techniques. It introduces concepts like redundancy, forward error correction, retransmission, linear block coding, Hamming codes, and cyclic redundancy checks (CRC). Specific error correction codes covered include Hamming codes, which use modulo-2 arithmetic to add redundant bits to detect and correct single bit errors. CRC codes are also discussed, which use cyclic codes and polynomial representations to detect errors by computing a syndrome value. The document provides information on generating and detecting errors for different codes.

1. ERROR DETECTION&ERROR CORRECTION 1 MSRIT INFORMATION SCIENCE

2. AMAK A-> ANKITA (1MS07IS133) M-> MAYANK (1MS07IS047) A-> ANSHUJ (1MS07IS011) K-> KRISH (1MS07IS038) 2 MSRIT INFORMATION SCIENCE

4. HAMMING CODE

5. CYCLIC REDUNDANCY CHECK(CRC)

6. IMPLEMENTATION OF HAMMING CODETABLE OF CONTENTS: 3 MSRIT INFORMATION SCIENCE

8. Burst error(Multiple)

9. Redundancy: Correction or detection of errors. INTRODUCTION 4 MSRIT INFORMATION SCIENCE

12. Adding : 0+0=0 0+1=1 1+0=1 1+1=0 Subt: 0-0=0 0-1=1 1-0=1 1-1=0 XOR operation: 1 0 1 1 0 1 1 1 0 0 0 1 0 1 0 6 MSRIT INFORMATION SCIENCE

14. k bit datawords

15. r redundant bits

16. n= k+r, n>k,n bit codeword.

17. 2k total datawords(equal to number of valid codewords.)

18. 2n total codewords

19. 2n -2k invalid codewords7 MSRIT INFORMATION SCIENCE

22. Need more number of redundant bits than for detection.

23. Involves error detection as well as finding the position(s) where error has occurred.8 MSRIT INFORMATION SCIENCE

24. Generation of codewords for each dataword: C(7,4) n ,k Codeword is generated by the generator which appends 3 redundant bits at the end of the dataword. Ro =a2 + a1 + a0 Modulo-2 R1= a3 + a2 + a1 Modulo-2 R2= a1+ a0 + a3 Modulo-2 HAMMING CODE GENERATION 9 MSRIT INFORMATION SCIENCE

25. A CRC CODE WITH C(7,4) 10 MSRIT INFORMATION SCIENCE

26. checker on the receiver side will generate a 3bit syndrome by the formulae given below: s0 = b2 + b1 + b0 + q0 modulo-2 s1 = b3 + b2 + b1 + q1 modulo-2 s2 = b1 + b0 + b3 + q2 modulo-2 If the syndrome i.e s2s1s0 is 000 then data is error free…or undetected. Otherwise, received codeword has an error(s). 11 MSRIT INFORMATION SCIENCE

27. MAGIC TABLE Depending upon the value of syndrome we can find the position of occurrence of error and then the bit position where error has occurred is flipped. 12 MSRIT INFORMATION SCIENCE

28. CODEWORD NOTATION ON SENDER’S AND RECEIVER’S SIDE a3 a2 a1 a0 R2 R1 R0 b3b2 b1 b0 q2 q1 q0 13 MSRIT INFORMATION SCIENCE

29. Number of bit change occurring between two codewords. 0 1 1 1 0 1 0 1 0 1 1 1 1 1 0 1 0 0 1 0 1 The total number of ones is equal to the number of bit changes between two codewords. HAMMING DISTANCE 14 MSRIT INFORMATION SCIENCE

30. Smallest Hamming Distance between all sets of codewords. Ex- d(0000000,0001101) = 3 d(0001100,0111001) = 4 d(0110100,0111001) =3 d(11111111,0000000) =7…. & so on.. Dmin= 3 for the above set of codewords. MINIMUM HAMMING DISTANCE 15 MSRIT INFORMATION SCIENCE

31. Suppose ‘s’ errors are to be detected, then dmin should be s+1. for the example taken, it can detect upto a maximum of 2 errors. Suppose ‘t’ errors are to be corrected, then the dmin should be 2t+1. in the above example, it can correct upto only 1 error. 16 MSRIT INFORMATION SCIENCE

32. Linear block code? Linear block code with an extra property: code word is cyclically rotated that generates another codeword. 1010110 is a codeword on rotating 0101101 which is another codeword. CYCLIC CODE 17 MSRIT INFORMATION SCIENCE

33. Type of linear block code which only detects errors. Its computation resembles a long division operation in which the quotient is discarded and the remainder becomes the result. CYCLIC REDUNDANCY CHECK(CRC) 18 MSRIT INFORMATION SCIENCE

34. CRC ENCODER AND DECODER 19 MSRIT INFORMATION SCIENCE

35. Encoder on sender’s side generates codeword. Dataword size is k bits. Desired codeword is n bits. Augment dataword by appending n-k 0’s. Divisor (predefined) of size n-k+1, divides augmented dataword in generator. Obtained remainder is appended to dataword. 20 MSRIT INFORMATION SCIENCE

36. The generated codeword is sent to receiver via some transmission medium. Decoder on receiver’s side checks for errors. The checker divides the codeword by the same divisor. This generates a remainder which is called a syndrome. If the syndrome is 0 then there is no error or the error is undetected. If syndrome is non zero, error has been detected and data is discarded. 21 MSRIT INFORMATION SCIENCE

37. Cyclic codes can be represented using polynomials. Special polynomials in which co-efficient can be either 0 or 1. The bit position of dataword indicates power of the polynomial. Ex:- 1 0 0 1 1 0 1 1 x7 x6 x5 x4 x3 x2 x1 x0 equivalent polynomial expression x7+x4+x3+x+1. POLYNOMIAL REPRESENTATION 22 MSRIT INFORMATION SCIENCE

38. The given dataword can be represented in polynomial terms. Multiply the dataword with xn-kto generate augmented dataword. The augmented dataword is divided by the generator polynomial g(x) and the resulting remainder is added to the augmented dataword. Note in division when we subtract we actually perform XOR operation. CODEWORD GENERATION 23 MSRIT INFORMATION SCIENCE

39. The divisor on the receiving side divides the received code word and generates a remainder. Remainder is also called as a syndrome. If the syndrome generated is 0 then there is no error in transmission or undetected error. Non zero syndrome means that error has been detected. No error correction is possible using CRC. ERROR DETECTION 24 MSRIT INFORMATION SCIENCE

42. To catch error of 1+xt the generator polynomial should not divide 1+xt for 0

43. Odd number of errorsGenerator polynomial should be a factor of x+1. 26 MSRIT INFORMATION SCIENCE

44. Polynomial should contain more than one term. Polynomial should have the x0 term equal to 1. Polynomial should contain x+1 as a factor. Polynomial should not divide 1+xt for 0<t<n-1. PROPERTIES OF GOOD GENERATOR POLYNOMIAL 27 MSRIT INFORMATION SCIENCE