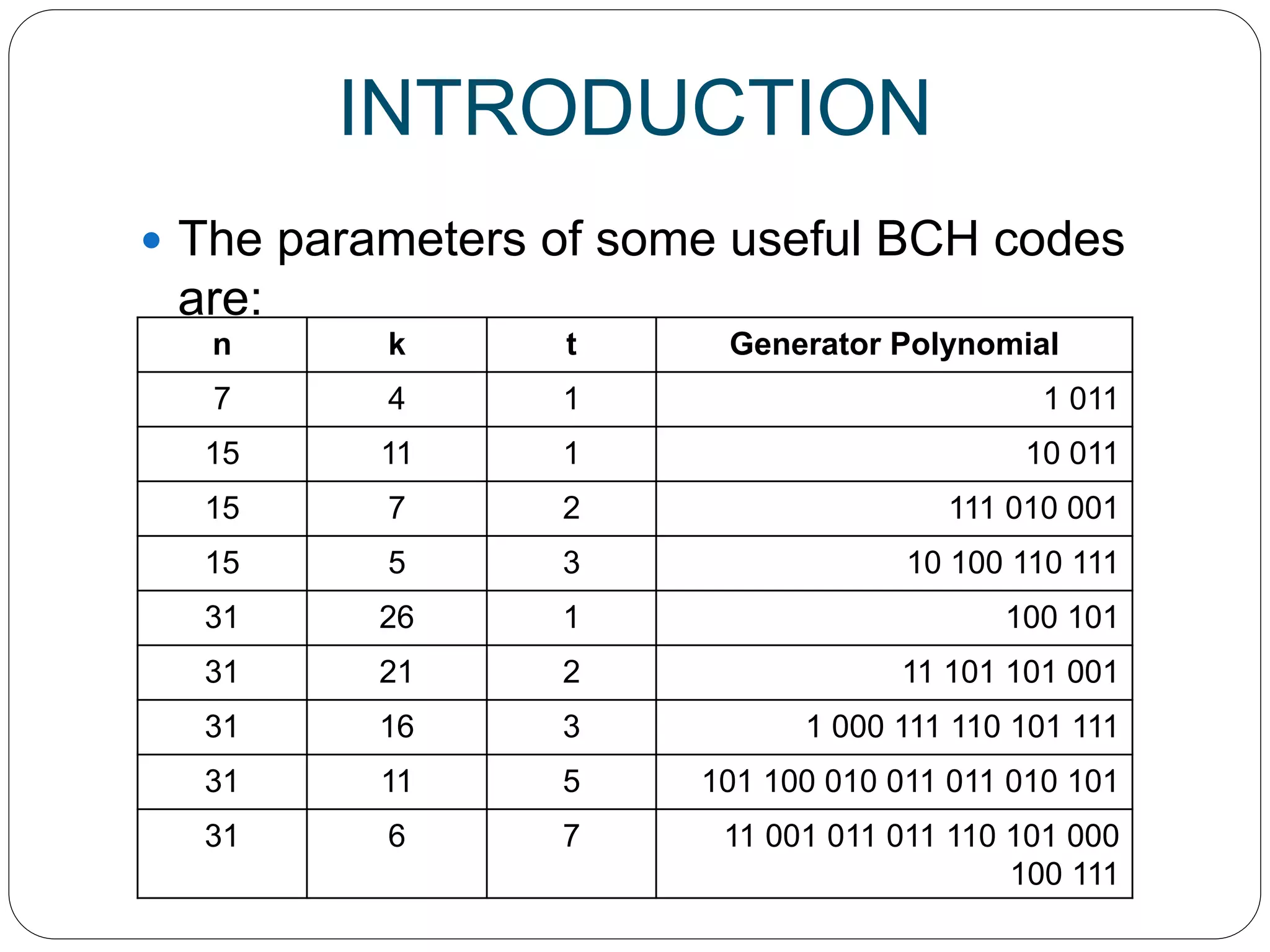
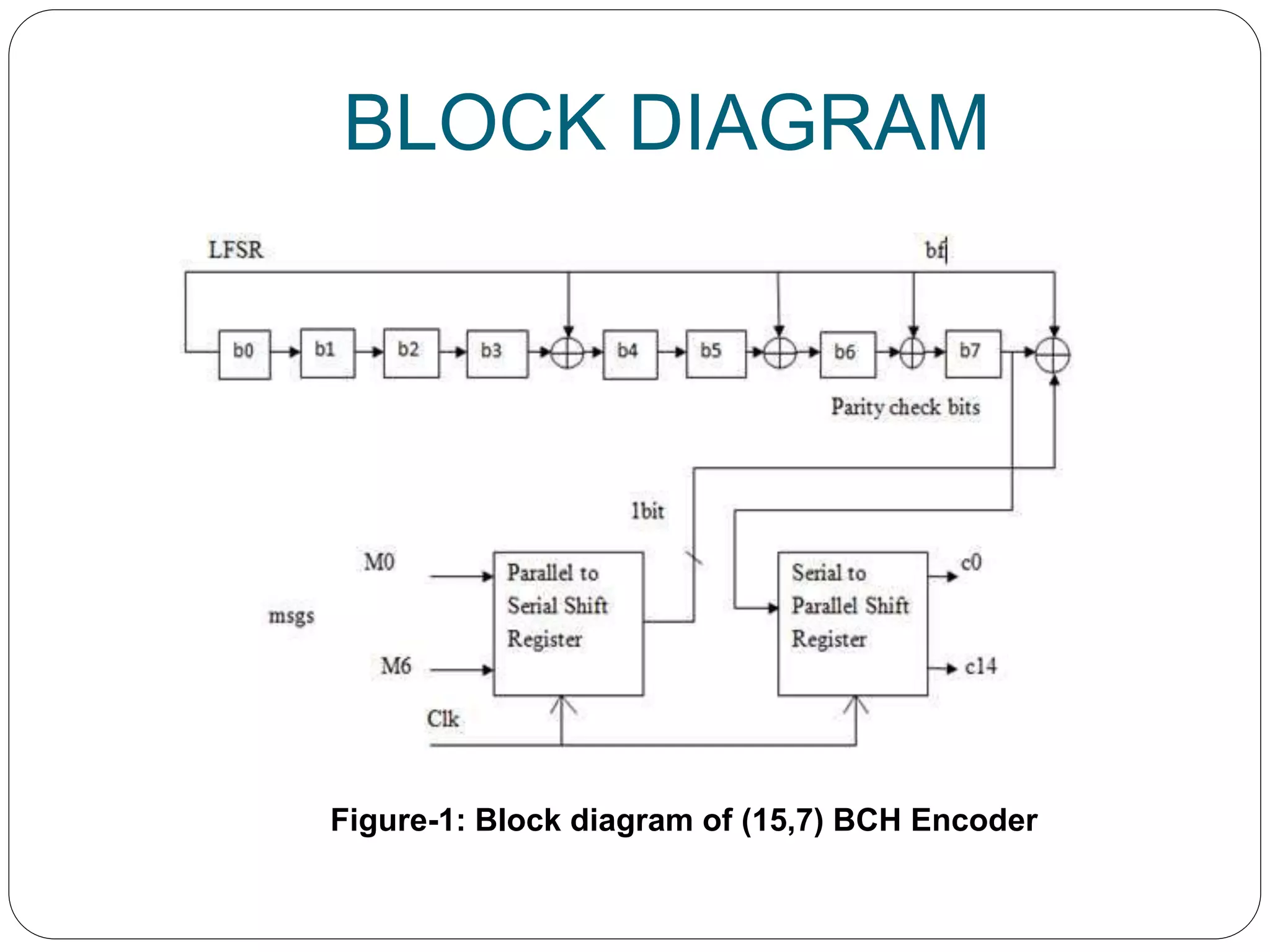
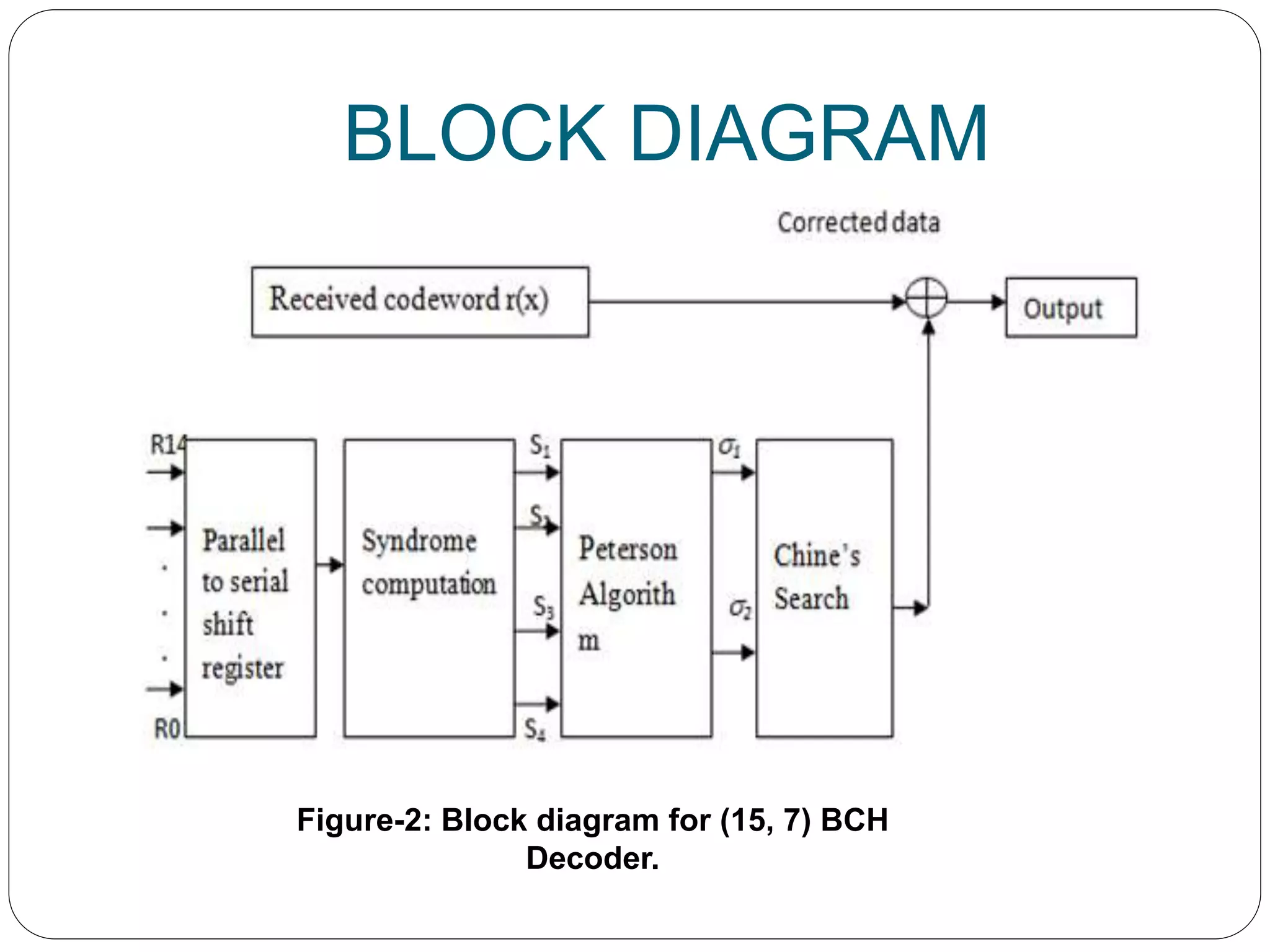
BCH codes are powerful cyclic error-correcting codes used to detect and correct multiple random errors in digital communications, characterized by flexible block lengths and control over code rate. They were discovered in the late 1950s and are particularly effective due to simple decoding methods, yet they can be complex to implement. Applications include satellite communications, digital media storage, and industry standards for video coding and data transmission.

1. BCH Codes
Information Theory &
Coding

2. OUTLINE
 INTRODUCTION
 BLOCK DIAGRAM
 EXAMPLE
 MERITS
 DEMERITS
 APPLICATIONS

3. •Powerful random error-correcting cyclic codes.
•Makes block size(n) smallest for given message
block(k) to obtain desired hamming distance.
•Discovered by Hocquenghem in 1959 and
independently by Bose and Chaudhuri in 1960.
•Most important subclass  Reed-Solomon (RS)
codes.
•Berlekamp’s iterative algorithm and Chien’s search
algorithm—most efficient decoding algorithms.
•In technical terms a BCH code is a
multilevel cyclic variable-length digital error-correcting
code used to correct multiple random error patterns.
INTRODUCTION

4. INTRODUCTION
 For positive pair of integers m≥3 and t, a (n, k) BCH
code has parameters:
 Block length: n = 2m – 1
 Number of check bits: n – k ≤ mt
 Minimum distance: dmin ≥ 2t + 1
 t<(2m – 1)/2 random errors detected and corrected.
 So also called ‘t-error correcting BCH code’.
 Major advantage is flexibility for block length and
code rate.

5.  Generator polynomial  specified in terms of its
roots from Galois Field GF(2k).
 g(x) has α,α2,…, α2t and their conjugates as its roots.
 We choose g(x) from xn + 1 polynomial factors by
taking xn-k as highest term.
INTRODUCTION

6.  The parameters of some useful BCH codes
are:
n k t Generator Polynomial
7 4 1 1 011
15 11 1 10 011
15 7 2 111 010 001
15 5 3 10 100 110 111
31 26 1 100 101
31 21 2 11 101 101 001
31 16 3 1 000 111 110 101 111
31 11 5 101 100 010 011 011 010 101
31 6 7 11 001 011 011 110 101 000
100 111
INTRODUCTION

7. BLOCK DIAGRAM
Figure-1: Block diagram of (15,7) BCH Encoder

8. BCH Encoder
 (15, 7) BCH Encoder.
 The 7 message bits (M0, M1….M6) are applied to the
parallel to serial shift register.
 The output of parallel to serial shift register will be
sent to (15, 7) BCH Encoder module.
 Using these message bits, parity bits are computed
and sent to serial to parallel shift register.
 Then parity bits are appended to original message bits
to obtain 15 bit encoded data.
 This entire encoding process requires 15 clock cycles.

9. Figure-2: Block diagram for (15, 7) BCH
Decoder.
BLOCK DIAGRAM

10. BCH Decoder
 (15, 7) BCH decoder.
 The decoding algorithm for BCH codes consists of
three major steps.
 Calculate the syndrome value Si, i=1,2,….,2t from
the received word r(x).
 Determine the error location polynomial s(x)
 Find the roots of s(x) and then correct the errors

11. EXAMPLE
 For a (31,21,2) BCH code:
 Encoder: t = 2
 g(x)=xⁿ+1=x³¹+1
=(x+1)(x¹⁰+x⁹+x⁸+x⁶+x⁵+x³+1)
(x²⁰+x¹⁷+x¹⁶+x¹³+x¹¹+x⁷+x⁶+x⁵+x²+x+1)
 Here highest order term for g(x) must be chosen as
xⁿ⁻ᵏ=x³¹⁻²¹=x¹⁰
 So g(x)= (x¹⁰+x⁹+x⁸+x⁶+x⁵+x³+1)

12.  Message D: (0110011)
 Data: d(x)=x⁵+x⁴+x+1
 So code C(x)=d(x).g(x)
= (x⁵+x⁴+x+1)(x¹⁰+x⁹+x⁸+x⁶+x⁵+x³+1)
= x¹⁵+2x¹⁴+2x¹³+x¹²+2x¹¹+4x¹⁰+3x⁹+2x⁸
+2x⁷+2x⁶+2x⁵+2x⁴+x³+x+1
= x¹⁵+x¹²+ x⁹+ x³+x+1
• Codeword, C: (1001001000001011)

13. MERITS
 The principal advantage is the ease with which they can be decoded
using ‘syndrome decoding’ method.
 Allows very simple electronic hardware to perform the task,
obviating the need for a computer, and meaning that a decoding
device may be made small and low-powered.
 Highly flexible, allowing control over block length and acceptable
error thresholds, meaning that a custom code can be designed to a
given specification
 Reed–Solomon codes, which are BCH codes, are used in
applications such as satellite communications, compact
disc players, DVDs, disk drives, and two-dimensional bar codes.
 BCH codes are also useful in theoretical computer science.
 Low amount of redundancy
 Easy to implement in hardware
 Widely used

14. DEMERITS
 Complexity
 Iterative and complex decoding algorithm
 Decoder cannot decide whether a decoded package
is false or not.

15. APPLICATIONS
 BCH Codes as Industry Standards:
 (511, 493) BCH code in ITU-T. Rec. H.261
“video codec for audiovisual service at kb/s”
a video coding standard used for video
conferencing and video phone.
n=511 m=9
k=493
n-k=18 t=2
 (40, 32) BCH code in ATM (Asynchronous
Transfer Mode) pp. 223-227.
is a shortened cyclic code that can correct
1-bit error and detect 2-bit errors.

16. THANK
YOU