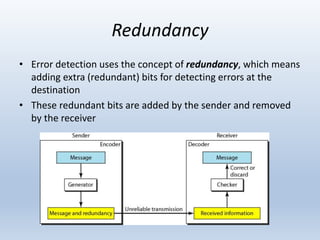
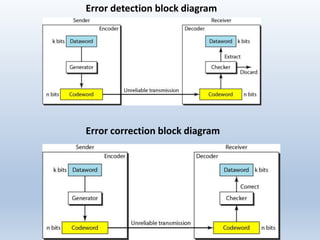
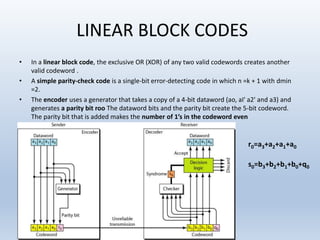
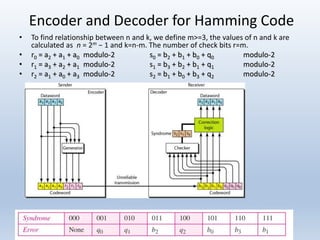
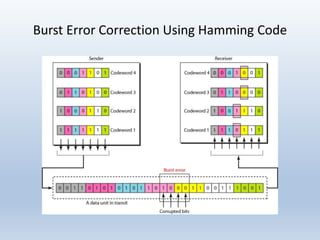
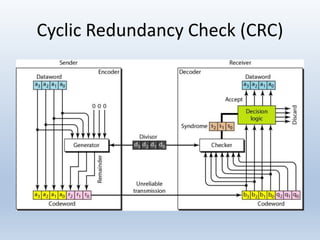
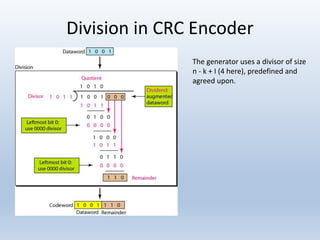
Chapter 10 covers error detection and correction in data communication, highlighting types of errors like single-bit and burst errors. It explains redundancy mechanisms for error detection and correction methodologies, including forward error correction and retransmission. Additionally, it discusses various coding techniques, Hamming distance for error detection/correction, cyclic redundancy checks, and checksum calculations.

1. Error Detection and correction
Chapter 10
Data communication and networks

2. Type of errors
• Only one bit of a given data unit
is changed
• The least likely type of error in
serial transmission
• Single-bit error can happen in
parallel transmission
Burst Error
• Two or more bits in the data
unit have changed
• Burst error does not necessarily
mean that the errors occur in
consecutive bits
• Most likely to happen in a serial
transmission
• Number of bits affected
depends on the data rate and
duration of noise
Single-Bit Error

3. Redundancy
• Error detection uses the concept of redundancy, which means
adding extra (redundant) bits for detecting errors at the
destination
• These redundant bits are added by the sender and removed
by the receiver

4. Error control
• Detection VS Correction
 Detection: error ? yes or no
 Correction: Need to know the exact number of bits that are corrupted,
and their location in the message
• Forward Error Correction VS Retransmission( backward error correction)
 Forward error correction is the process in which the receiver tries to
guess the message by using redundant bits
 if the number of errors is small. Correction by retransmission is a
technique in which the receiver detects the occurrence of an error and
asks the sender to resend the message. Resending is repeated until a
message arrives that the receiver believes is error-free
• In modulo-N arithmetic, we use only the integers in the range
0 to N-1, inclusive.

5. Block Coding
• Divide the message into blocks, each of k bits, called datawords.
• Add r redundant bits to each block to make the length n = k + r. The
resulting n-bit blocks are called codewords
• 2n - 2k codewords that are not used. We call these codewords invalid or
illegal
• we need more redundant bits for error correction than for error detection
• Example: 4B/5B block coding
– k = 4 and n = 5.
– 2k = 16 datawords and 2n = 32 codewords.

6. Error Detection
1. The receiver receives 011 which is a
valid codeword. The receiver extracts
the dataword 01 from it.
2. The codeword is corrupted during
transmission, and 111 is received.
This is not a valid codeword and is
discarded.
3. The codeword is corrupted during
transmission, and 000 is received.
This is a valid codeword. The receiver
incorrectly extracts the dataword 00.
Two corrupted bits have made the
error undetectable.
Error Correction
• The sender creates the codeword
01011. The codeword is corrupted
during transmission, and 01001 is
received. receiver finds an error has
occurred , assuming that there is only
1 bit corrupted .
• Comparing the received codeword
with the 1st codeword in the table
(01001 versus 00000), the receiver
decides that the 1st codeword is not
the one that was sent because there
are 2 different bits. (the same for 3rd
or 4th one in the table)
• The original codeword must be the
2nd one in the table because this is
the only one that differs from the
received codeword by 1 bit.

7. Error detection block diagram
Error correction block diagram

8. Hamming distance
• Hamming distance between two words x and y as d(x, y).
• The Hamming distance between two words is the number of differences
between corresponding bits .
• Example: Hamming distance d(10101, 11110) is 3
• The minimum Hamming distance is the smallest Hamming distance
between all possible pairs in a set of words .
• for below example dmin = 2
• Three parameters to define the coding schemes
– Codeword size n
– Dataword size k
– The minimum Hamming distance dmin
• Coding scheme C(n, k) with a separate expression for dmin

9. Hamming distance
• Minimum distance for error detection
 If ‘s’ errors occurs during transmission, the Hamming
distance between the sent codeword and received
codeword is ‘s’.
If our code is to detect up to ‘s’ errors, the minimum
distance between the valid codewords must be ‘s+1’, so
that the received codeword does not match a valid
codeword.
dmin = s + 1.
• Minimum Distance for Error Correction
 To guarantee correction of up to “t” errors in all cases, the
minimum Hamming distance in a block code must be
 dmin = 2t+ 1.

10. LINEAR BLOCK CODES
• In a linear block code, the exclusive OR (XOR) of any two valid codewords creates another
valid codeword .
• A simple parity-check code is a single-bit error-detecting code in which n =k + 1 with dmin
=2.
• The encoder uses a generator that takes a copy of a 4-bit dataword (ao, aI' a2' and a3) and
generates a parity bit roo The dataword bits and the parity bit create the 5-bit codeword.
The parity bit that is added makes the number of 1’s in the codeword even
r0=a3+a2+a1+a0
s0=b3+b2+b1+b0+q0

11. Different situations of occurrence of
error in linear block coding
• No error occurs; the received codeword is 10111. The syndrome is
0. The dataword 1011 is created.
• One single-bit error changes a1, The received codeword is 10011.
The syndrome is 1. No dataword is created.
• One single-bit error changes ro The received codeword is 10110.
The syndrome is 1. No dataword is created. Note that although
none of the dataword bits are corrupted, no dataword is created .
• An error changes ro and second error changes a3 The received
codeword is 00110. The syndrome is 0. The dataword 0011 is
created at the receiver. Note that here the dataword is wrongly
created due to the syndrome value.
• Three bits- a3, a2, a1-are changed by errors. The received
codeword is 01011. The syndrome is 1. The dataword is not
created.
• A simple parity-check code can detect an odd number of errors.

12. Encoder and Decoder for Hamming Code
• To find relationship between n and k, we define m>=3, the values of n and k are
calculated as n = 2m − 1 and k=n-m. The number of check bits r=m.
• r0 = a2 + a1 + a0 modulo-2 s0 = b2 + b1 + b0 + q0 modulo-2
• r1 = a3 + a2 + a1 modulo-2 s1 = b3 + b2 + b1 + q1 modulo-2
• r2 = a1 + a0 + a3 modulo-2 s2 = b1 + b0 + b3 + q2 modulo-2

13. Burst Error Correction Using Hamming Code

14. Cyclic Redundancy Check (CRC)

15. Division in CRC Encoder
The generator uses a divisor of size
n - k + I (4 here), predefined and
agreed upon.

16. Division in CRC Decoder

17. Cyclic Code Analysis
• Dataword: d(x) Syndrome: s(x) Error: e(x)
Codeword: c(x) Generator: g(x)
• In a cyclic code,
1. If s(x)≠0, one or more bits is corrupted.
2. If s(x) =0, either
a. No bit is corrupted. or
b. Some bits are corrupted, but the decoder failed to detect them
• Received codeword =c(x) + e(x)
• (Received codeword)/g(x) = c(x)/g(x) + e(x)/g(x) = s(x)
• First term: no remainder
• Second term:
 if it is not equal to zero then there is some error
 If it is equal to zero that means, either e(x)=0 or e(x) is exactly divisible by
g(x) refers to no error scenario.

18. Cyclic Code Analysis
• In a cyclic code, those e(x) errors that are divisible by g(x) are not caught .
• If the generator g(x) has more than one term and the coefficient of X0 is 1,
all single errors can be caught.
• If a generator cannot divider “x^t+1” (t between 0 and n - 1), then all
isolated double errors can be detected.
• A generator that contains a factor of “x + 1” can detect all odd-numbered
errors.
• Burst error’s ( L == length of error ; r== no of check bits )
1. All burst errors with L <= r will be detected
2. All burst errors with L =r + 1 will be detected with
probability 1 - (1/2)^(r-1)
3. All burst errors with L > r + 1 will be detected with
probability 1-(1/2)^r
Example g(x) = x^14 + x^3 + 1 then r = 14

19. Checksum
• (7, 11, 12, 0, 6), we send (7, 11, 12,0,6,36),
where 36 is the sum of the original numbers .
• We send the negative (complement) of the
sum, called the checksum. In this case, we
send (7, 11, 12,0,6,-36).
• Complement of “x” = (2^n – 1) –x : n bit’s

20. Checksum: Example
• The sender initializes the checksum to 0 and adds all data items
and the checksum. However, 36 cannot be expressed in 4 bits. The
extra two bits are wrapped and added with the sum to create the
wrapped sum value 6. The sum is then complemented, resulting in
the checksum value 9 (15 − 6 = 9).

21. Internet Checksum

22. Example on internet check sum
DATA (32 bit) 10110011101010110101101011010101
Sender side
• 1011001110101011  seg 1
• 0101101011010101  seg 2
• 0000111010000000  seg1 +seg 2
• 1  carry
• 0000111010000001  sum
• 1111000101111110  checksum { 1’s complement of sum }
• Send the “ DATA + checksum “ to the receiver
Receiver side
• 1011001110101011  seg 1
• 0101101011010101  seg 2
• 1111000101111110  checksum
• 1111111111111110  seg 1 + seg 2 + checksum
• 1  carry
• 1111111111111111  sum’
• 0000000000000000  checksum’ { 1’s complement of sum’ }