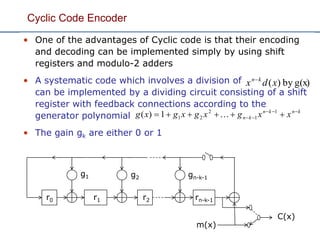
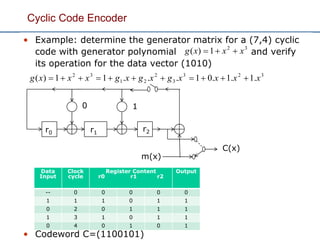
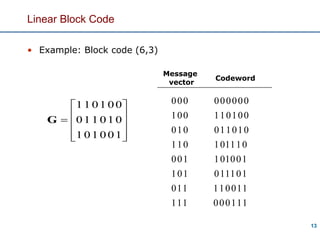
This document discusses channel coding and linear block codes. Channel coding adds redundant bits to input data to allow error detection and correction at the receiver. Linear block codes divide the data into blocks, encode each block into a larger codeword, and use a generator matrix to map message blocks to unique codewords. The codewords can be detected and sometimes corrected using a parity check matrix. Hamming codes are a type of linear block code that can correct single bit errors. The document provides examples of encoding data using generator matrices and decoding using syndrome values and parity check matrices. It also discusses how the minimum distance of a code determines its error detection and correction capabilities.





![Linear Block Code
• In Systematic block code
• In matrix form
7
,...,1,
.........
.........
,22,11,
,12121111
nknknfor imc
and
mpmpmpc
mpmpmpc
ii
kknkkkkn
kkn
100
010
001
][
,21
,22221
,11211
21
knkkk
kn
kn
k
ppp
ppp
ppp
mmmC](https://image.slidesharecdn.com/unit5dcerrorcodingclasssmg-191011220545/85/Digital-Communication-Channel-Coding-7-320.jpg)
![Linear Block Code
•
8
mGC
matrixParity)(
matrixidentity
matrixGenerator][
knk
kkk
nkk
P
I
IPG
100
010
001
,21
,22221
,11211
knkkk
kn
kn
k
ppp
ppp
ppp
IPG](https://image.slidesharecdn.com/unit5dcerrorcodingclasssmg-191011220545/85/Digital-Communication-Channel-Coding-8-320.jpg)



![Linear Block Code
• In polynomial form the codeword c(x) can be written as
c(x) = m(x) g(x)
• where m(x) is the message polynomial and g(x) is the
generator polynomial, G is the generator matrix.
• G = [P | I],
• where Pi = Remainder of [xn-k+i-1/g(x)] for i=1, 2, .., k, and I
is unit matrix.
14
knkkk
kn
kn
k ppp
ppp
ppp
P
P
P
P
,21
,22221
,11211
2
1
](https://image.slidesharecdn.com/unit5dcerrorcodingclasssmg-191011220545/85/Digital-Communication-Channel-Coding-14-320.jpg)




![Error detection and error correction capabilities of LBC
• Theorem: A LBC with a minimum distance dmin can detect
upto dmin -1 errors and correct upto [(dmin -1)/2] errors.
Where [(dmin -1)/2] denotes the largest integer not greater than
(dmin -1)/2.
• Proof:
Let C be the transmitted codeword and
R is the received codeword.
Let C’ be the any other codeword in the code.
• Then the Hamming distance between codeword d(C,C’),
d(C,R) and d(C’,R) satisfy
d(C,R)+ d(C’,R) ≥ d(C,C’) … 1
Let the received vector consist of t errors i.e. d(C,R)=t
Let dmin be the minimum distance of the code
d(C,C’) ≥ dmin](https://image.slidesharecdn.com/unit5dcerrorcodingclasssmg-191011220545/85/Digital-Communication-Channel-Coding-19-320.jpg)