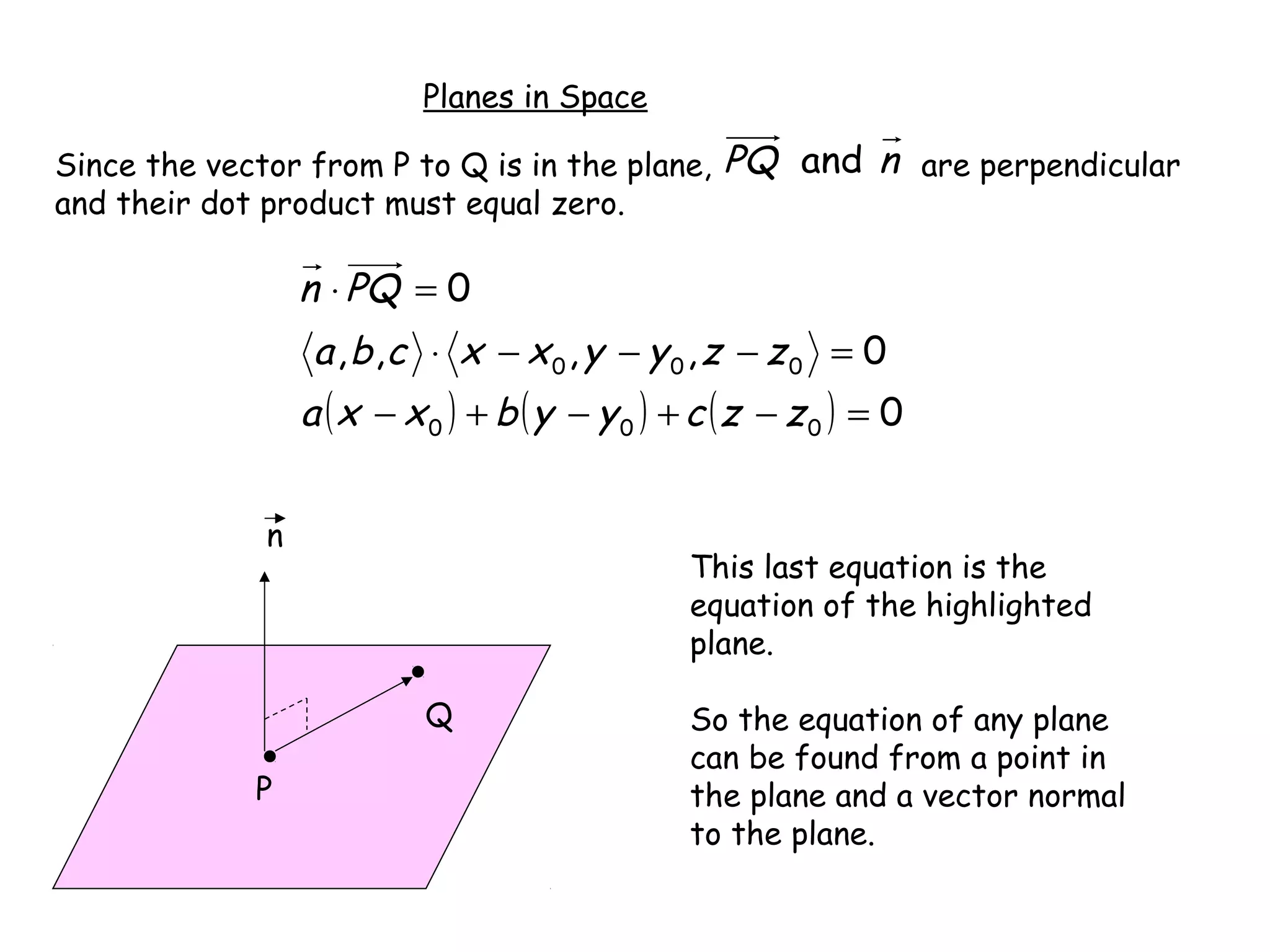
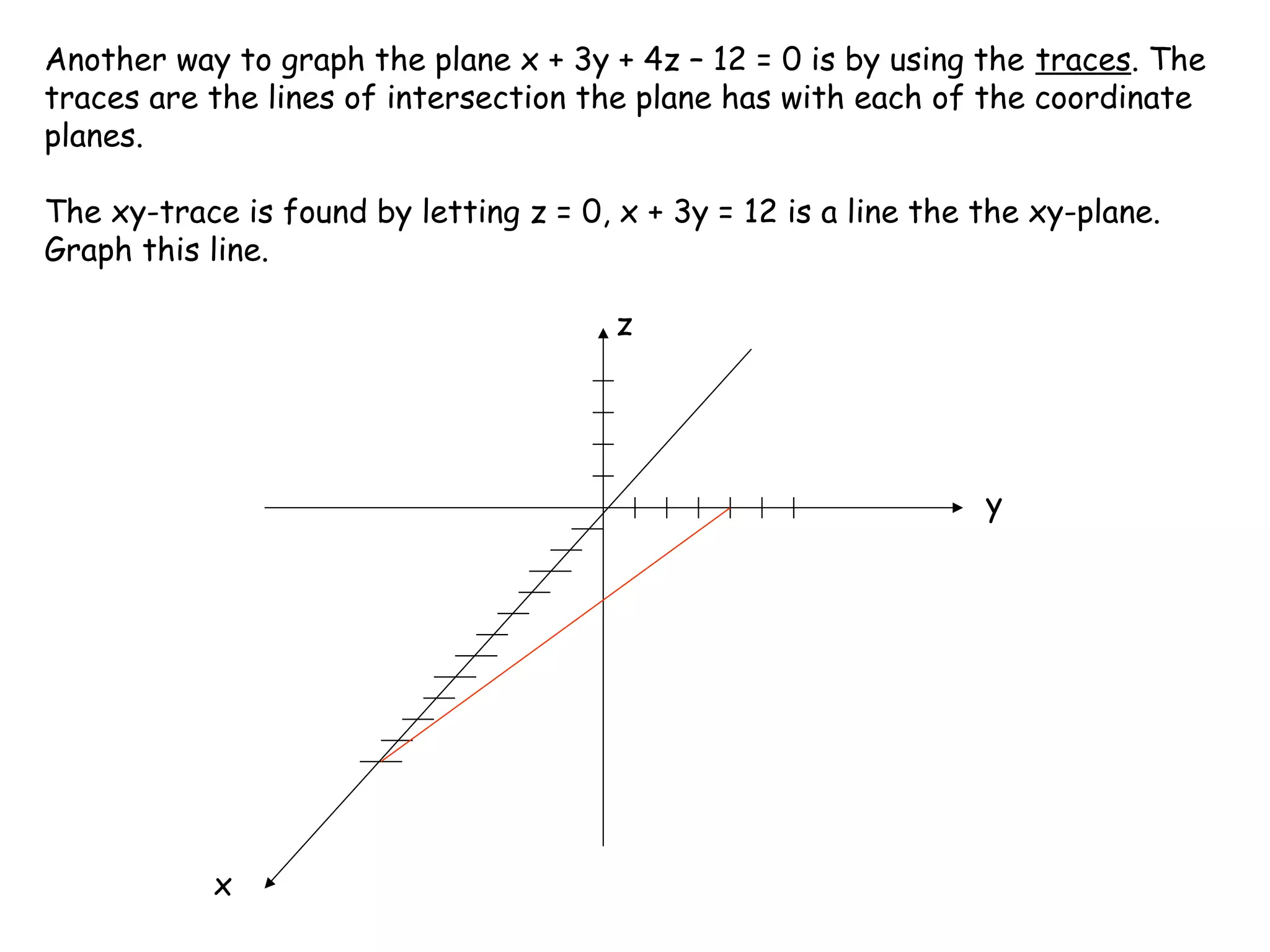
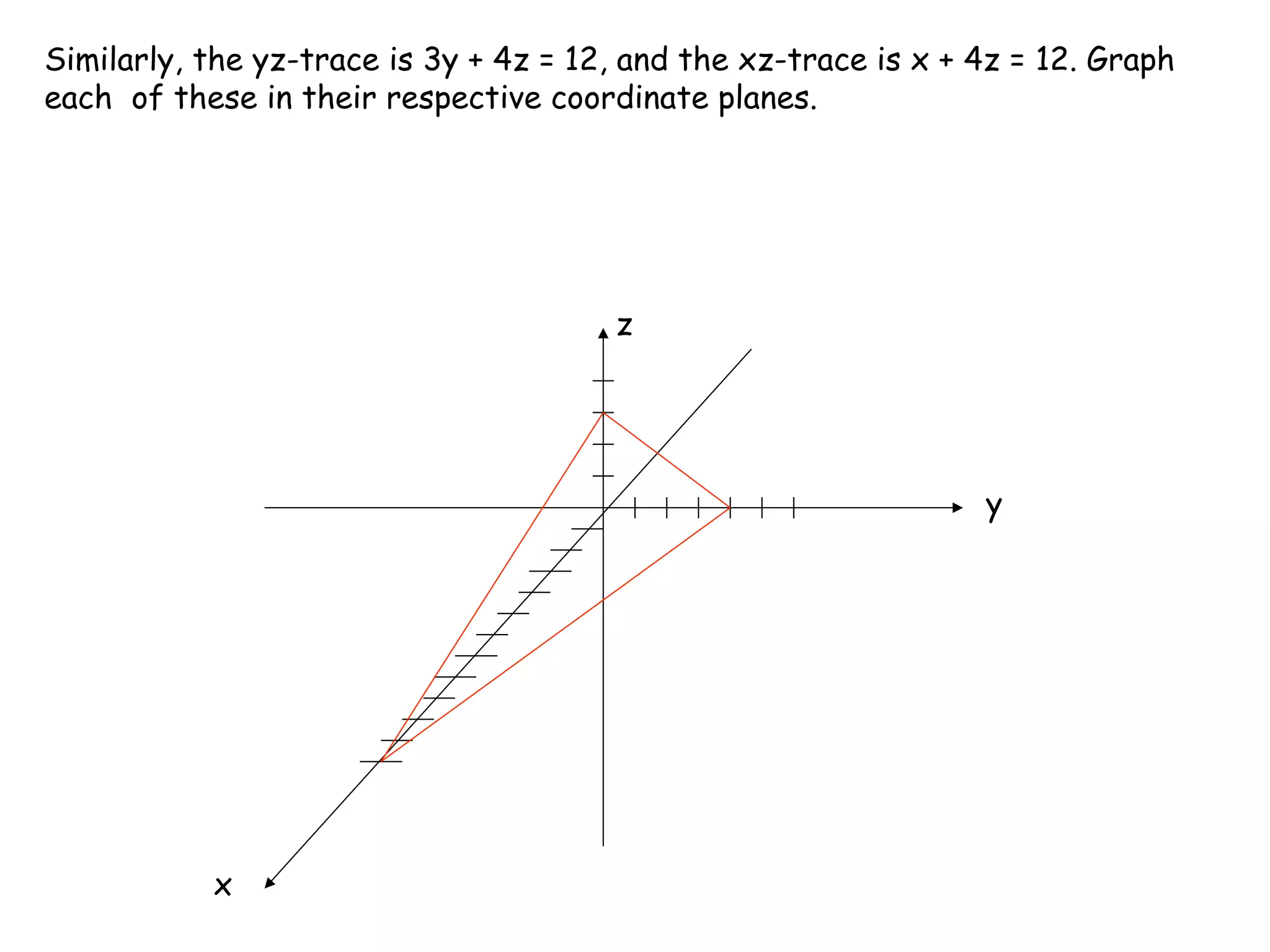
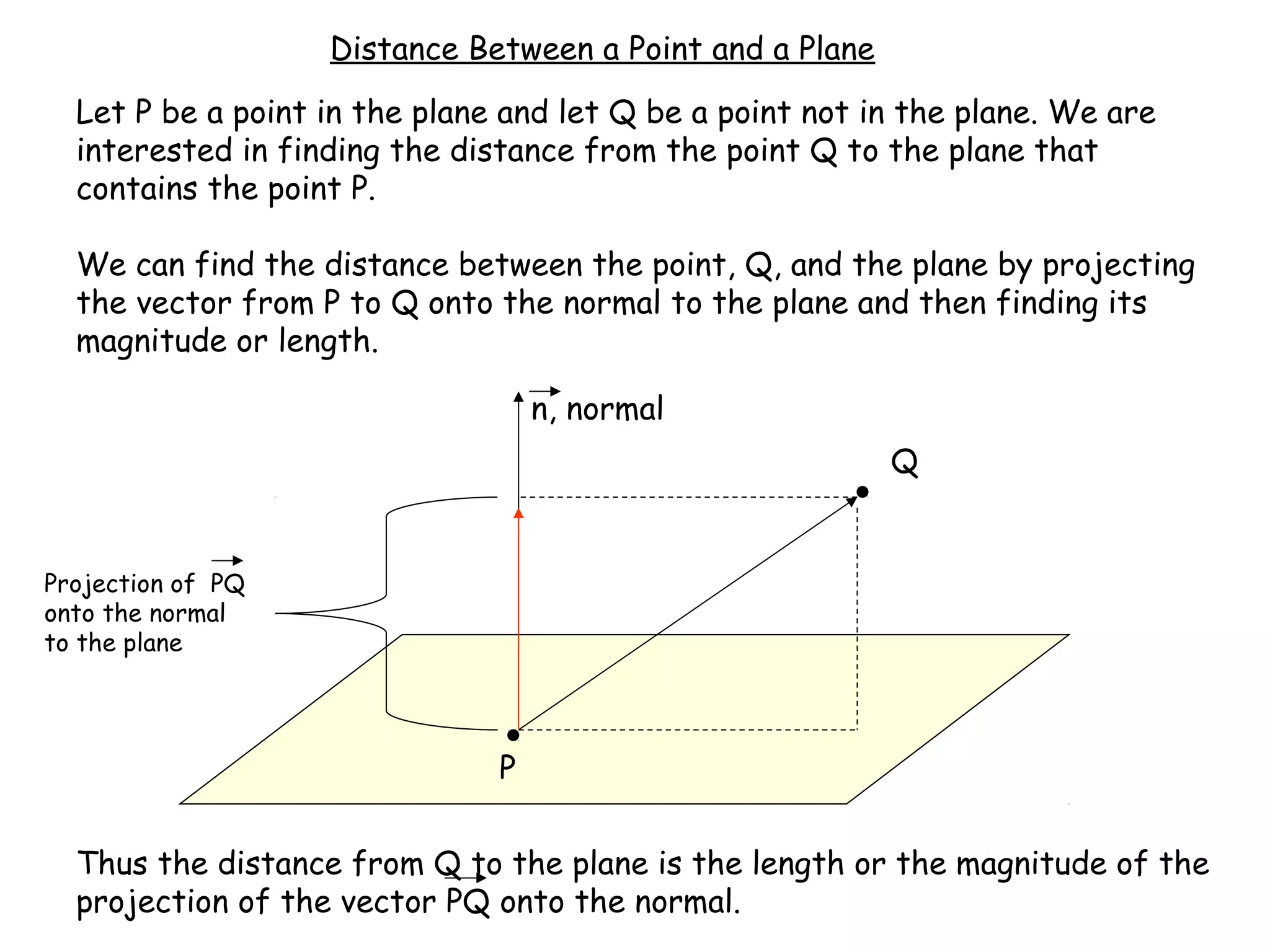
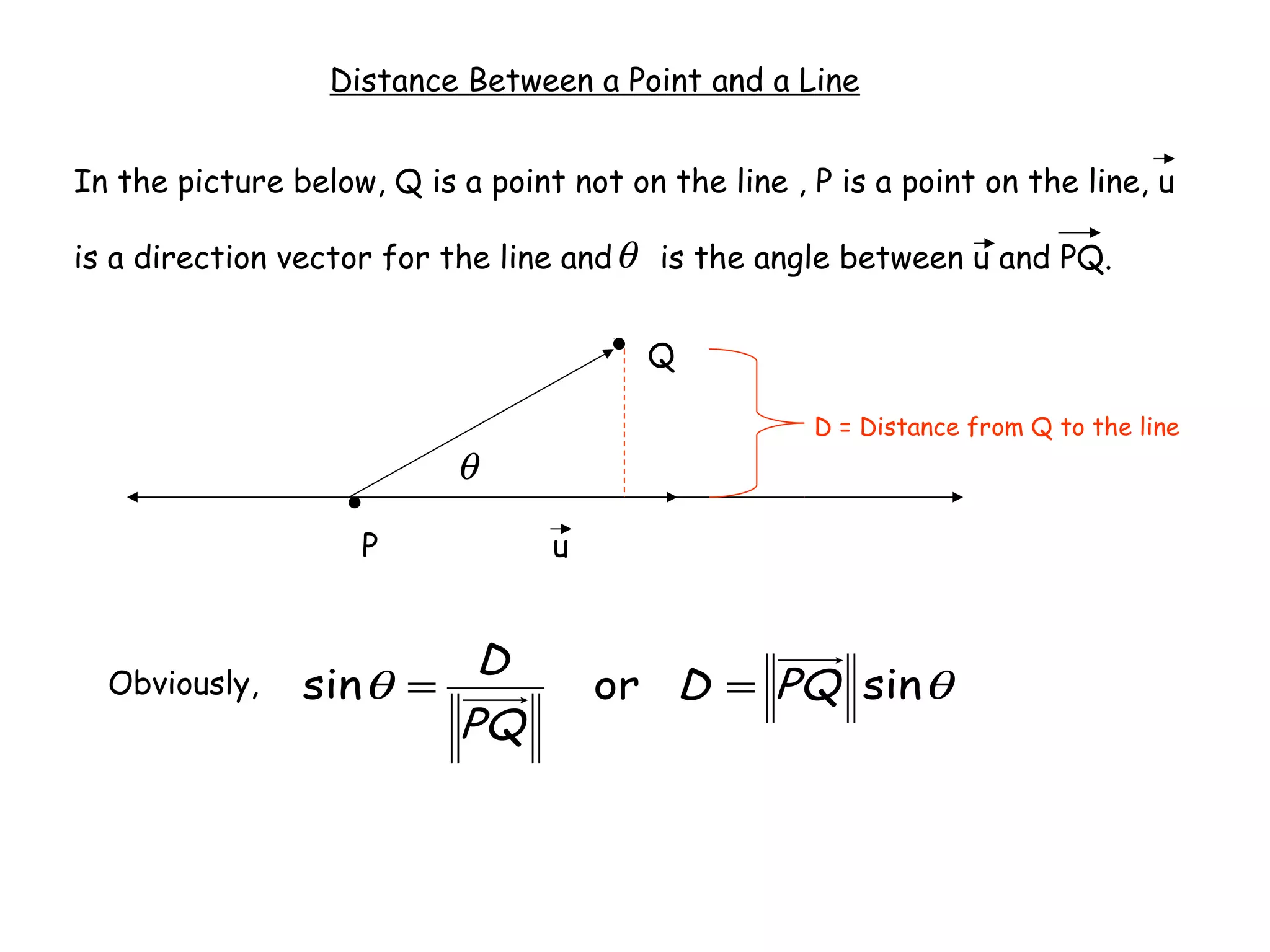
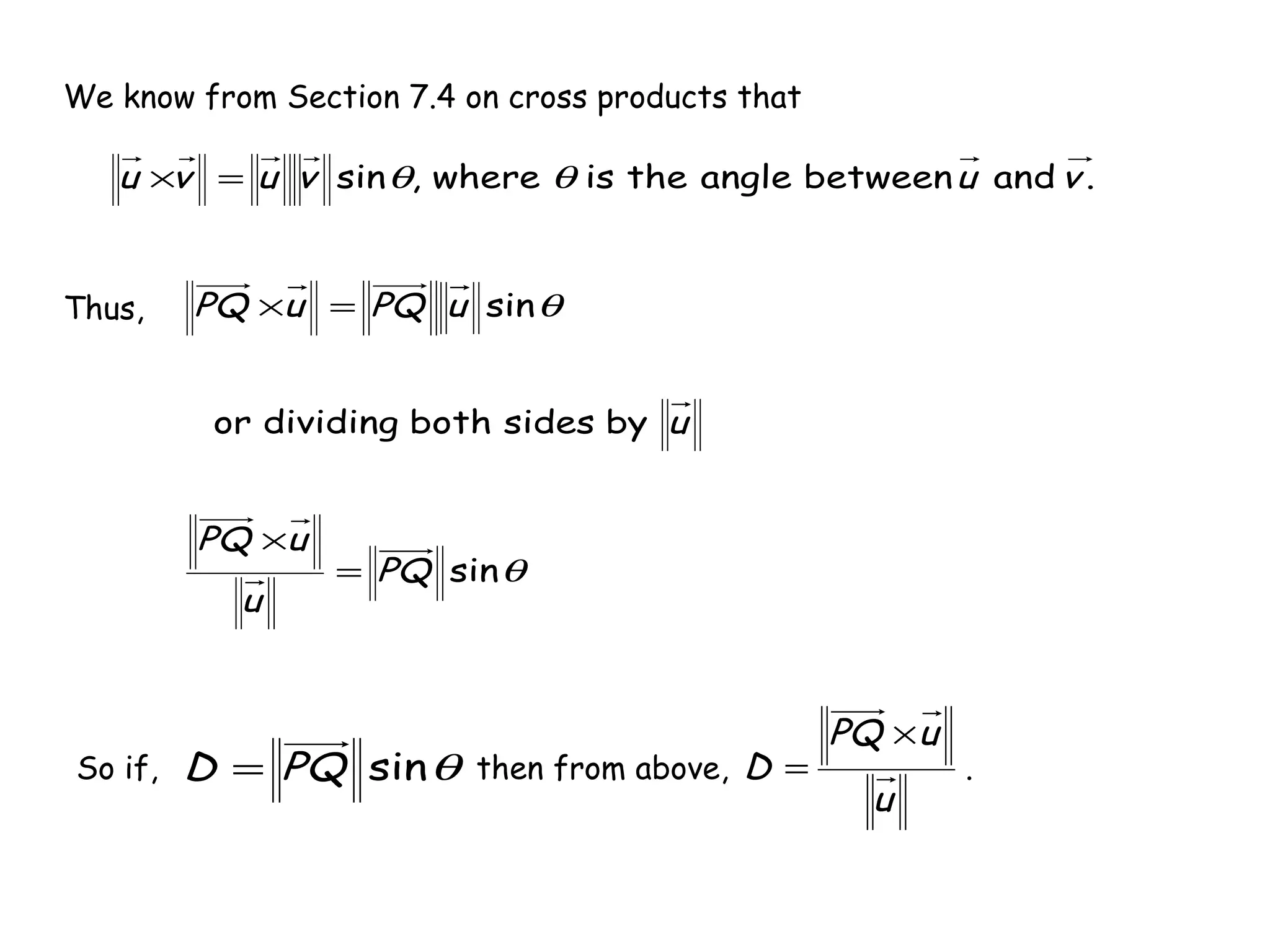
The document discusses lines and planes in 3D space. It defines lines as being determined by a point and direction vector, and gives parametric and symmetric equations to represent lines. Planes are defined by a point and normal vector, with standard and general forms for their equations. Methods are provided for finding the intersection of lines or planes, as well as the distance between a point and plane or line. Examples demonstrate finding equations of lines and planes, sketching planes, and determining relationships between lines or planes.

1. Chapter 7: Vectors and the
Geometry of Space
Section 7.5
Lines and Planes in Space
Written by Karen Overman
Instructor of Mathematics
Tidewater Community College, Virginia Beach Campus
Virginia Beach, VA
With Assistance from a VCCS LearningWare Grant

2. In this lesson you will learn:
o Lines in Space
o Parametric equations for a line
o Symmetric equations for a line
o Relationships between lines in space
o Planes in Space
o Standard form and General form of a plane
o Sketching planes using traces
oThe line of intersection of two planes
o Distances in Space
o The distance between a point and a plane
o The distance between a point and a line

3. Lines in Space
Previously you have studied lines in a two-dimensional coordinate system.
These lines were determined by a point and a direction or the slope.
In 3-dimensional space, a line will also be determined by a point and a
direction, except in 3-dimensional space the direction will be given by a
parallel vector, called the direction vector.

4. Lines in Space
To determine the equation of the line passing through the point P
and parallel to the direction vector, , we will use our
knowledge that parallel vectors are scalar multiples. Thus, the vector
through P and any other point Q on the line is a scalar multiple
of the direction vector, .
( )000 ,, zyx
cbav ,,=
( )zyx ,,
cbav ,,=
In other words,
( )
ctbtatzzyyxx
tcbat
,,,,
or
scalarnumberrealanyiswhere,,,PQ
000 =−−−
=

5. Equations of Lines in
Space
Equate the respective components and there are three equations.
ctzzbtyyatxx
ctzzbtyyatxx
+=+=+=
=−=−=−
000
000
and,
or
and,
These equations are called the parametric equations of the line.
If the components of the direction vector are all nonzero, each
equation can be solved for the parameter t and then the three can be
set equal.
c
zz
b
yy
a
xx 000 −
=
−
=
−
These equations are called the symmetric equations of the line.

6. Equations of Lines in
Space
A line passing through the point P and parallel to the vector,
is represented by the parametric equations:
And if all three components of the direction vector are nonzero, the line
is also represented by the symmetric equations:
ctzzbtyyatxx +=+=+= 000 and,
cbav ,,=
( )000 ,, zyx
c
zz
b
yy
a
xx 000 −
=
−
=
−

7. Example 1: Find the parametric and symmetric equations of the line passing
through the point (2, 3, -4) and parallel to the vector, <-1, 2, 5> .
Solution: Simply use the parametric and symmetric equations for any line given
a point on the line and the direction vector.
Parametric Equations:
tztytx 54and23,2 +−=+=−=
Symmetric Equations:
5
4
2
3
1
2 +
=
−
=
−
− zyx

8. Example 2: Find the parametric and symmetric equations of the line passing
through the points (1, 2, -2) and (3, -2, 5).
Solution: First you must find the direction vector which is just finding the
vector from one point on the line to the other. Then simply use the
parametric and symmetric equations and either point.
7,4,225,22,13vectordirection −=+−−−=v
tztytx 72and42,21:equationsparametric +−=−=+=
7
2
4
2
2
1
:equationssymmetric
+
=
−
−
=
− zyx
Notes:
1. For a quick check, when t = 0 the parametric equations give the point
(1, 2, -2) and when t = 1 the parametric equations give the point (3, -2, 5).
2. The equations describing the line are not unique. You may have used the
other point or the vector going from the second point to the first point.

9. Relationships Between Lines
In a 2-dimensional coordinate system, there were three possibilities when
considering two lines: intersecting lines, parallel lines and the two were
actually the same line.
In 3-dimensional space, there is one more possibility. Two lines may be skew,
which means the do not intersect, but are not parallel. For an example see
the picture and description below.
If the red line is down in the xy-
plane and the blue line is above the
xy-plane, but parallel to the xy-
plane the two lines never intersect
and are not parallel.

10. Example 3: Determine if the lines are parallel or identical.
tz
ty
tx
21
42
25:2Line
−=
+−=
−=
tz
ty
tx
+=
−=
+=
4
22
3:1Line
Solution: First look at the direction vectors: 2,4,2and1,2,1 21 −−=−= vv
Since , the lines are parallel.
Now we must determine if they are identical. So we need to determine
if they pass through the same points. So we need to determine if the
two sets of parametric equations produce the same points for
different values of t.
Let t=0 for Line 1, the point produced is (3, 2, 4). Set the x from Line
2 equal to the x-coordinate produced by Line 1 and solve for t.
12 2vv −=
122253 =→−=−→−= ttt
Now let t=1 for Line 2 and the point (3, 2, -1) is produced. Since the z-
coordinates are not equal, the lines are not identical.

11. Example 4: Determine if the lines intersect. If so, find the point of
intersection and the cosine of the angle of intersection.
tz
ty
tx
−=
+=
−=
2
53
4:2Line
tz
ty
tx
−=
−=
+=
4
2
23:1Line
Solution: Direction vectors:
Since , the lines are not parallel. Thus they either intersect or
they are skew lines.
1,5,11,2,2 21 −−=−−= vv
12 vkv ⋅≠
Keep in mind that the lines may have a point of intersection or a common
point, but not necessarily for the same value of t. So equate each
coordinate, but replace the t in Line 2 with an s.
stz
sty
stx
−=−
+=−
−=+
24:
532:
423:
System of 3 equations with 2
unknowns – Solve the first 2 and
check with the 3rd
equation.

12. Solution to Example 4 Continued:
Solving the system, we get t = 1 and s = -1.
Line 1: t = 1 produces the point (5, -2, 3)
Line 2: s = -1 produces the point (5, -2, 3)
The lines intersect
at this point.
Recall from lesson 7.3 on the dot product,
numerator.theinvalueabsoluteuseweso
,90thanlessbeshouldlinesngintersectitwobetweenθangleThe
andbetweenangletheishere,cos

vuw
vu
vu
θθ
⋅
⋅
=

13. Solution to Example 4 Continued:
( ) ( ) ( ) ( )
706.0
39
11
279
1102
cos
151122
1,5,11,2,2
cos
222222
≈
−
=
⋅
+−−
=
−++−⋅−+−+
−−⋅−−
=
θ
θ
Thus,

14. Planes in Space
In previous sections we have looked at planes in space. For example, we looked
at the xy-plane, the yz-plane and the xz-plane when we first introduced 3-
dimensional space.
Now we are going to examine the equation for a plane. In the figure below P,
, is a point in the highlighted plane and is the vector
normal to the highlighted plane.
( )000 ,, zyx cban ,,=
n
P
Q
For any point Q,
in the plane, the vector from P
to Q ,
is also in the plane.
( )zyx ,,
000 ,, zzyyxxPQ −−−=

15. Planes in Space
Since the vector from P to Q is in the plane, are perpendicular
and their dot product must equal zero.
n
P
Q
This last equation is the
equation of the highlighted
plane.
So the equation of any plane
can be found from a point in
the plane and a vector normal
to the plane.
nPQ and
( ) ( ) ( ) 0
0,,,,
0
000
000
=−+−+−
=−−−⋅
=⋅
zzcyybxxa
zzyyxxcba
PQn

16. Standard Equation of a Plane
The standard equation of a plane containing the point and having
normal vector, is
Note: The equation can be simplified by using the distributive property and
collecting like terms.
This results in the general form:
( )000 ,, zyx
cban ,,=
( ) ( ) ( ) 0000 =−+−+− zzcyybxxa
0=+++ dczbyax

17. Example 5: Given the normal vector, <3, 1, -2> to the plane containing the
point (2, 3, -1), write the equation of the plane in both standard form and
general form.
Solution: Standard Form ( ) ( ) ( ) 0000 =−+−+− zzcyybxxa
( ) ( ) ( ) 0123123 =+−−+− zyx
To obtain General Form, simplify.
01123
or
022363
=−−+
=−−−+−
zyx
zyx

18. Example 6: Given the points (1, 2, -1), (4, 0,3) and (2, -1, 5) in a plane, find the
equation of the plane in general form.
Solution: To write the equation of the plane we need a point (we have three) and
a vector normal to the plane. So we need to find a vector normal to the plane.
First find two vectors in the plane, then recall that their cross product will be a
vector normal to both those vectors and thus normal to the plane.
Two vectors: From (1, 2, -1) to (4, 0, 3): < 4-1, 0-2, 3+1 > = <3,-2,4>
From (1, 2, -1) to (2, -1, 5): < 2-1, -1-2, 5+1 > = <1,-3,6>
Their cross product:
kjkji
kji
7147140
631
423 −−=−−=
−
−
( ) ( ) ( )
032
or
021714
01721410
=−+
=+−−
=+−−−−
zy
zy
zyxEquation of the plane:

19. Sketching Planes in Space
If a plane intersects all three coordinate planes (xy-plane, yz-plane and the
xz-plane), part of the plane can be sketched by finding the intercepts and
connecting them to form the plane.
For example, let’s sketch the part of the plane, x + 3y + 4z – 12 = 0 that
appears in the first octant.
The x-intercept (where the plane intersects the x-axis) occurs when both y
and z equal 0, so the x-intercept is (12, 0, 0). Similarly the y-intercept is
(0, 4, 0) and the z-intercept is (0, 0, 3).
Plot the three points on the coordinate system and then connect each pair
with a straight line in each coordinate plane. Each of these lines is called a
trace.
The sketch is shown on the next slide.

20. Sketch of the plane x + 3y + 4z – 12 = 0 with intercepts, (12, 0, 0), (0, 4, 0)
and (0, 0, 3).
y
x
z
Now you can see the triangular
part of the plane that appears
in the first octant.

21. y
x
z
Another way to graph the plane x + 3y + 4z – 12 = 0 is by using the traces. The
traces are the lines of intersection the plane has with each of the coordinate
planes.
The xy-trace is found by letting z = 0, x + 3y = 12 is a line the the xy-plane.
Graph this line.

22. y
x
z
Similarly, the yz-trace is 3y + 4z = 12, and the xz-trace is x + 4z = 12. Graph
each of these in their respective coordinate planes.

23. Example 7: Sketch a graph of the plane 2x – 4y + 4z – 12 = 0.
Solution: The intercepts are (6, 0, 0), (0, -3, 0) and (0, 0, 3). Plot each of
these and connect each pair with a straight line.

24. y
x
z
Example 7: Sketch a graph of the plane 2x – 4y + 4z – 12 = 0.
Solution: The intercepts are (6, 0, 0), (0, -3, 0) and (0, 0, 3). Plot each of
these and connect each pair with a straight line.
Hopefully you can see the part of the
plane we have sketched appears on the
negative side of the y-axis.

25. Not all planes have x, y and z intercepts. Any plane whose equation is missing
one variable is parallel to the axis of the missing variable. For example,
2x + 3y – 6 = 0 is parallel to the z-axis. The xy trace is 2x + 3y = 6, the yz
trace is y = 2 and the xz trace is x = 3.
Part of the plane is outlined in red.
More on Sketching Planes
Any plane whose equation is missing two variables is parallel to the
coordinate plane of the missing variables. For example, 2x – 6 = 0 or x = 3 is
parallel to the yz-plane.
The plane is outlined in
blue and is at the x value
of 3.

26. Intersecting Planes
Any two planes that are not parallel or identical will intersect in a line and to
find the line, solve the equations simultaneously.
For example in the figure above, the white plane and the yellow plane intersect
along the blue line.

27. Example 8: Find the line of intersection for the planes x + 3y + 4z = 0
and x – 3y +2z = 0.
( )
zyzy
zyxzyx
zyxzyx
3
1
or026
023023
0430431
−
==−−
=+−→=+−
=−−−→=++⋅−
Back substitute y into one of the first equations and solve for x.
zx
zzx
zzx
3
04
04
3
1
3
−=
=+−
=+




 −
⋅+
Finally if you let z = t, the parametric equations for the line are
tztytx =
−
=−= and
3
1
,3
Solution: To find the common intersection, solve the equations simultaneously.
Multiply the first equation by –1 and add the two to eliminate x.

28. Distance Between a Point and a Plane
P
Q
n, normal
Projection of PQ
onto the normal
to the plane
Thus the distance from Q to the plane is the length or the magnitude of the
projection of the vector PQ onto the normal.
Let P be a point in the plane and let Q be a point not in the plane. We are
interested in finding the distance from the point Q to the plane that
contains the point P.
We can find the distance between the point, Q, and the plane by projecting
the vector from P to Q onto the normal to the plane and then finding its
magnitude or length.

29. Distance Between a Point and a Plane
If the distance from Q to the plane is the length or the magnitude of the
projection of the vector PQ onto the normal, we can write that
mathematically:
PQprojn
=planethetoQfromDistance
Now, recall from section 7.3,
n
n
nPQ
PQprojn
⋅










⋅
= 2
So taking the magnitude of this vector, we get:
n
nPQ
n
n
nPQ
n
n
nPQ
PQprojn
⋅
=⋅
⋅
=⋅










⋅
= 22

30. Distance Between a Point and a Plane
The distance from a plane containing the point P to a point Q not in the
plane is
n
nPQ
PQprojD n
⋅
==
where n is a normal to the plane.

31. Example 9: Find the distance between the point Q (3, 1, -5) to the plane
4x + 2y – z = 8.
Solution: We know the normal to the plane is <4, 2, -1> from the general
form of a plane. We can find a point in the plane simply by letting x and y
equal 0 and solving for z: P (0, 0, -8) is a point in the plane.
Thus the vector, PQ = <3-0, 1-0, -5-(-8)> = <3, 1, 3>
Now that we have the vector PQ and the normal, we simply use the formula
for the distance between a point and a plane.
( )
4.2
21
11
1416
3212
124
1,2,43,1,3
222
≈=
++
−+
=
−++
−⋅
=
⋅
==
D
n
nPQ
PQprojD n

32. Let’s look at another way to write the distance from a point to a plane. If
the equation of the plane is ax + by + cz + d = 0, then we know the normal
to the plane is the vector, <a, b, c> .
Let P be a point in the plane, P = and Q be the point not in the
plane, Q = . Then the vector,
( )111 ,, zyx
( )000 ,, zyx
101010 ,, zzyyxxPQ −−−=
So now the dot product of PQ and n becomes:
( ) ( ) ( )
111000
101010
101010 ,,,,
czbyaxczbyax
zzcyybxxa
zzyyxxcbanPQ
−−−++=
−+−+−=
−−−⋅=⋅
Note that since P is a point on the plane it will satisfy the equation of the
plane, so and the dot
product can be rewritten:
111111 or0 czbyaxddczbyax −−−==+++
dczbyaxnPQ +++=⋅ 000

33. Thus the formula for the distance can be written another way:
The Distance Between a Point and a Plane
The distance between a plane, ax + by + cz + d = 0 and a point Q
is
222
000
cba
dczbyax
PQprojD n
++
+++
==
( )000 ,, zyx
Now that you have two formulas for the distance between a point and a plane,
let’s consider the second case, the distance between a point and a line.

34. Distance Between a Point and a Line
In the picture below, Q is a point not on the line , P is a point on the line, u
is a direction vector for the line and is the angle between u and PQ.
P
Q
u
D = Distance from Q to the line
Obviously, θθ sinorsin PQD
PQ
D
==
θ
θ

35. We know from Section 7.4 on cross products that
.andbetweenangletheiswhere,sin vuvuvu θθ=×
Thus,
θ
θ
sin
bysidesbothdividingor
sin
PQ
u
uPQ
u
uPQuPQ
=
×
=×
So if, then from above, .θsinPQD =
u
uPQ
D
×
=

36. Distance Between a Point and a Line
The distance, D, between a line and a point Q not on the line is given by
u
uPQ
D
×
=
where u is the direction vector of the line and P is a point on the line.

37. Example 10: Find the distance between the point Q (1, 3, -2) and the line
given by the parametric equations:
tztytx 23and1,2 +=−−=+=
Solution: From the parametric equations we know the direction vector, u is
< 1, -1, 2 > and if we let t = 0, a point P on the line is P (2, -1, 3).
Thus PQ = < 2-1, -1-3, 3-(-2) > = < 1, -4, 5 >
Find the cross product:
( )
( )
12.2
2
9
6
27
211
333
222
222
≈==
+−+
++−
=
×
=
u
uPQ
D
kji
kji
uPQ 333
211
541 ++−=
−
−=×
Using the distance formula:

38. You have three sets of practice problems for this lesson in
Blackboard under Chapter 7, Lesson 7.5 Parts A, B and C.