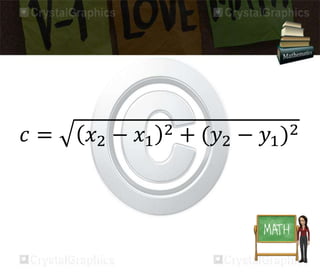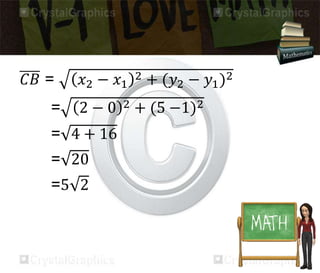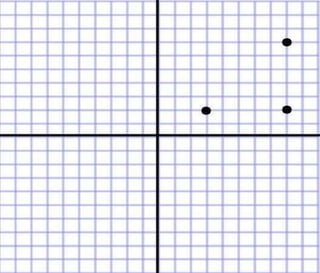
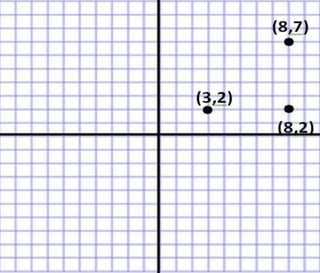
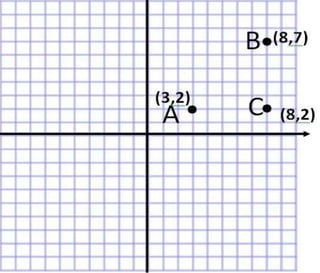
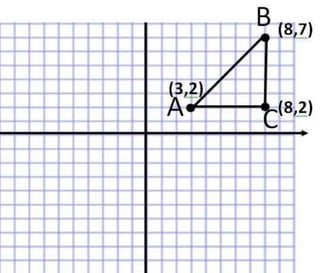
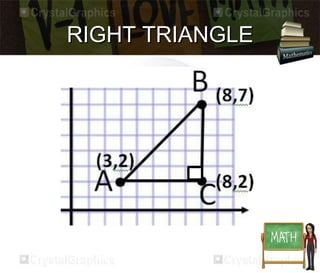
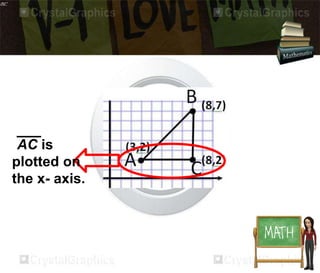
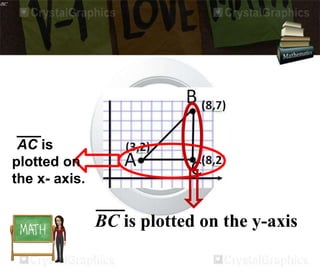
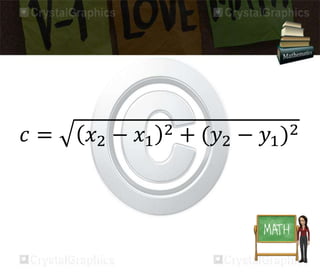
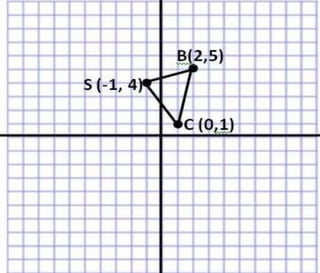
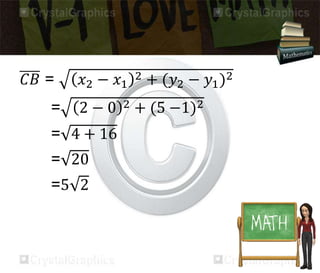
The document discusses the distance formula. It explains how to calculate the distance between two points (x1, y1) and (x2, y2) using the formula: Distance = √(x2 - x1)2 + (y2 - y1)2. It provides an example of calculating the distance between points (3,2) and (8,7), which equals 5. The document also contains instructions for students to practice using the distance formula to find distances between various point coordinates, and assignments to graph points and calculate distances using the formula.

1. DISTANCE FORMULA

2. Plot these coordinates on
our Cartesian plane.
(3,2)
(8,7)
(8,2)

8. RIGHT TRIANGLE

9. AC is
plotted on
the x- axis.

10. Find the difference of the two
coordinates in x axis.
x2-x1
x2=8
x1=3
=8 – 3
=5

11. AC is
plotted on
the x- axis.
BC is plotted on the y-axis

12. Find the difference of the two
coordinates in x axis.
y2-y1
y2=7
y1=2
=7 – 2
=5

13. PYTHAGOREAN
THEOREM
c
a
b

14. 푐 = 푥2 − 푥1
2 + (푦2 − 푦1)2

15. DISTANCE FORMULA

16. SUBSTITUTION METHOD
By substitution:
퐷 = 푥2 − 푥1
2 + (푦2 − 푦1)2
퐷 = 5 2 + 5 2
퐷 = 50

17. ACTIVITY #1
• Graph and show that the following
coordinates forms an isosceles
triangle by using the distance
formula.
S (-1,4)
C (0,1)
B (2,5)

21. 퐶퐵 = 푥2 − 푥1
2 + (푦2 − 푦1)2
= 2 − 0 2 + (5 −1)2
= 4 + 16
= 20
=5 2

22. 퐵푆 = 푥2 − 푥1
2 + (푦2 − 푦1)2
= 2 + 1 2 + (5 −4)2
= 10

23. QUIZ#6
Get ½ crosswise sheet of paper and
answer the following.
Find the distance between the given
points.
1. (0,9) and (0,13)
2. (4,5) and (-3,5)
3. (8,1) and (8,-2)
4. (1,0) and (5,2)
5. (5,-4) and (1,-1)

24. ASSIGNMENT
A. Graph and Find the distance using
distance formula.
I (-4,6) and V (2,5)
Y (-1,6) and S (5, 10)
B. Make a research on midpoint and
give at least 2 examples.