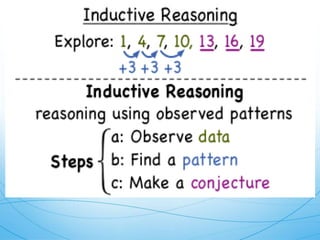
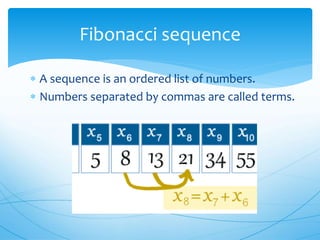
This document outlines key concepts in mathematical logic, including problem-solving strategies, inductive and deductive reasoning processes, and notable sequences like Fibonacci and Pascal's triangle. It also introduces George Polya's four principles for effective problem-solving: understanding the problem, devising a plan, carrying out the plan, and reviewing the process. Various exercises and references are provided to facilitate learning and application of these concepts.

1. By Prof. Liwayway Memije-Cruz
Problem
Solving and
Reasoning

2. Mathematical Logic
 Mathematical logic is a
subfield of mathematics
exploring the
applications of formal
logic to mathematics.
 A statement or
proposition, is a
declarative statement
that is either true or
false, but not both.

3. Solve:

4. 1. When asked how old she was, Mara replied “In two years I will be
twice as old as I was five years ago”. How old is she?
2 . If you have two coins totaling 11p, and one of the coins is not a
penny, what are the two coins?
3. Divide 40 by half and add ten. What is the answer?
4. To the nearest cubic centimeter, how much soil is there in a 3m x
2m x 2m hole?
5. A farmer has 15 cows, all but 8 die. How many does he have left?
6. The ages of a mother and her graduate son add up to 66. The
mother’s age is the son’s age reversed. How old are they?
7. The amount of water flowing into a tank doubles every minute.
The tank is full in an hour. When is the tank half full?
Mathematical Logic Test

5. Inductive Reasoning
 Uses specific examples to reach a general conclusion
called conjecture.
 a logical process in which multiple premises, all believed
true or found true most of the time, are combined to
obtain a specific conclusion.
 often used in applications that involve prediction,
forecasting, or behavior.
 not logically rigorous. Imperfection can exist and
inaccurate conclusions can occur.
 moves from the particular to the general. It gathers
together particular observations in the form of premises,
then it reasons from these particular premises to a
general conclusion.

7. 1. Mara leaves for school at 7:00 a.m. Mara is always on
time. Mara assumes, then, that she will always be on
time if she leaves at 7:00 a.m.
2. Two-thirds of the students at BSU receive student
aid. Therefore, two-thirds of all college students
receive student aid.
3. All children in the day care center like to play with
Legos. All children, therefore, enjoy playing with
Legos.
There are varying degrees of strength and weakness in inductive
reasoning, and various types including statistical syllogism, arguments
from example, causal inferences, simple inductions, and inductive
generalizations. They can have part to whole relations, extrapolations, or
predictions.

8. 1. Read and analyze Examples 1 – 4, pp.
43-46 of Mathematics in the Modern
World.
2. https://www.jobtestprep.co.uk/images/
free-pdf/free-logical-reasoning-
questions-answers.pdf
Exercises on Inductive Reasoning

9. Deductive Reasoning
 process of reaching a
general conclusion by
applying general
assumptions, procedures
and principles.
 is a logical process in which
a conclusion is based on
the concordance of
multiple premises that are
generally assumed to be
true.
syllogism
 The Greek philosopher
Aristotle, who is
considered the father of
deductive reasoning,
wrote the following
classic example:
 All men are mortal.
 Socrates is a man.
 Therefore, Socrates is
mortal.

10.  or deduction, is one of the two basic types of logical inference. A
logical inference is a connection from a first statement (a
“premise”) to a second statement (“the conclusion”) for which
the rules of logic show that if the first statement is true, the
second statement should be true.
 Examples:
 Premise: Socrates is a man, and all men are mortal.
 Conclusion: Socrates is mortal.
 Premise: This dog always barks when someone is at the door,
and the dog didn’t bark.
 Conclusion: There’s no one at the door.
 Premise: Sam goes wherever Ben goes, and Ben went to the
library.
 Conclusion: Sam also went to the library.
Deductive Reasoning

11.  Read, study and solve examples 5 and 6
in your book
Exercises:

12. Problem Solving with Patterns

13. Fibonacci sequence
 A sequence is an ordered list of numbers.
 Numbers separated by commas are called terms.

14. Fibonacci Numbers

15. Jacques Philippe Marie Binet
 a French mathematician,
physicist and astronomer
born in Rennes; he died in
Paris, France, in 1856.
 made significant
contributions to number
theory, and the
mathematical foundations of
matrix algebra.
 Binet's Formula expressing
Fibonacci numbers in closed
form is named in his honour,
although the same result
was known to Abraham de
Moivre a century earlier.

16. Binet’s Formula

17. Blaise Pascal
 a French mathematician,
physicist, inventor, writer
and Catholic theologian.
 Known for his Pascal
triangle

18. Pascal's Triangle
 One of the most
interesting Number
Patterns is Pascal's
Triangle (named after
Blaise Pascal, a famous
French Mathematician
and Philosopher). To
build the triangle, start
with "1" at the top, then
continue placing
numbers below it in a
triangular pattern.

19. History of Pascal's Triangle
Properties of Pascal's Triangle

20. Primes
 When you look at
Pascal's Triangle, find
the prime numbers
that are the first
number in the row.
That prime number is
a divisor of every
number in that row.


21. Powers of 2
 Now let's take a look at
powers of 2. If you notice,
the sum of the numbers is
Row 0 is 1 or 2^0. Similiarly,
in Row 1, the sum of the
numbers is 1+1 = 2 = 2^1. If
you will look at each row
down to row 15, you will
see that this is true. In fact,
if Pascal's triangle was
expanded further past Row
15, you would see that the
sum of the numbers of any
nth row would equal to 2^n

22. Fibonacci's Sequence
 If you take the
sum of the
shallow diagonal,
you will get the
Fibonacci
numbers.

23. Fractal
 If you shade all the
even numbers, you
will get a fractal.
This is also the
recursive of
Sierpinski's
Triangle.

24. Polya’s Problem Solving Strategy
 George Pólya was a
Hungarian
mathematician.
 In 1945 George Polya
published the book
 How To Solve It
 which quickly became
 his most prized
publication. It sold over
one million copies and
has been translated
 into 17 languages

25. Polya’s Problem Solving Strategy

26. Polya’s First Principle: Understand the
problem
Polya taught teachers to ask students questions such
as:
• Do you understand all the words used in stating the
problem?
• What are you asked to find or show?
• Can you restate the problem in your own words?
• Can you think of a picture or diagram that might
help you understand the problem?
• Is there enough information to enable you to find a
solution?

27. Polya’s Second Principle: Devise a plan
 Polya mentions that there
are many reasonable
ways to solve problems.
The skill at choosing an
appropriate strategy is
best learned by solving
many problems. You will
find choosing a strategy
increasingly easy. A
partial list of strategies is
included:
 Guess and check
 Look for a pattern
 Make an orderly list
 Draw a picture
 Eliminate possibilities
 Solve a simpler problem
 Use symmetry
 Use a model
 Consider special cases
 Work backwards
 Use direct reasoning
 Use a formula
 Solve an equation
 Be ingenious

28. This step is usually easier than devising
the plan. In general, all you need is care
and patience, given that you have the
necessary skills. Persist with the plan that
you have chosen. If it continues not to
work discard it and choose another.
Don’t be misled, this is how mathematics
is done, even by professional
Polya’s Third Principle: Carry out the
plan

29. Polya’s Fourth Principle: Look back
Polya mentions that much can be
gained by taking the time to reflect
and look back at what you have
done, what worked, and what didn’t.
Doing this will enable you to predict
what strategy to use to solve future
problems.

30.  Read and study the examples on Polya’s
strategy from pp. 55 – 60
 Read and answer Exercises Set 3 from
pp. 60-62
Exercises

31.  https://whatis.techtarget.com/definition/inductive-reasoning
 https://www.jobtestprep.co.uk/free-inductive-reasoning-
examples
 https://www.jobtestprep.co.uk/images/free-pdf/free-logical-
reasoning-questions-answers.pdf
 https://whatis.techtarget.com/definition/deductive-reasoning
 https://artofproblemsolving.com/wiki/index.php?title=Binet%27s_
Formula
 http://www.milefoot.com/math/discrete/sequences/binetformula
.htm
 http://jwilson.coe.uga.edu/EMAT6680Su12/Berryman/6690/Berry
manK-Pascals/BerrymanK-Pascals.html
 https://math.berkeley.edu/~gmelvin/polya.pdf
References: