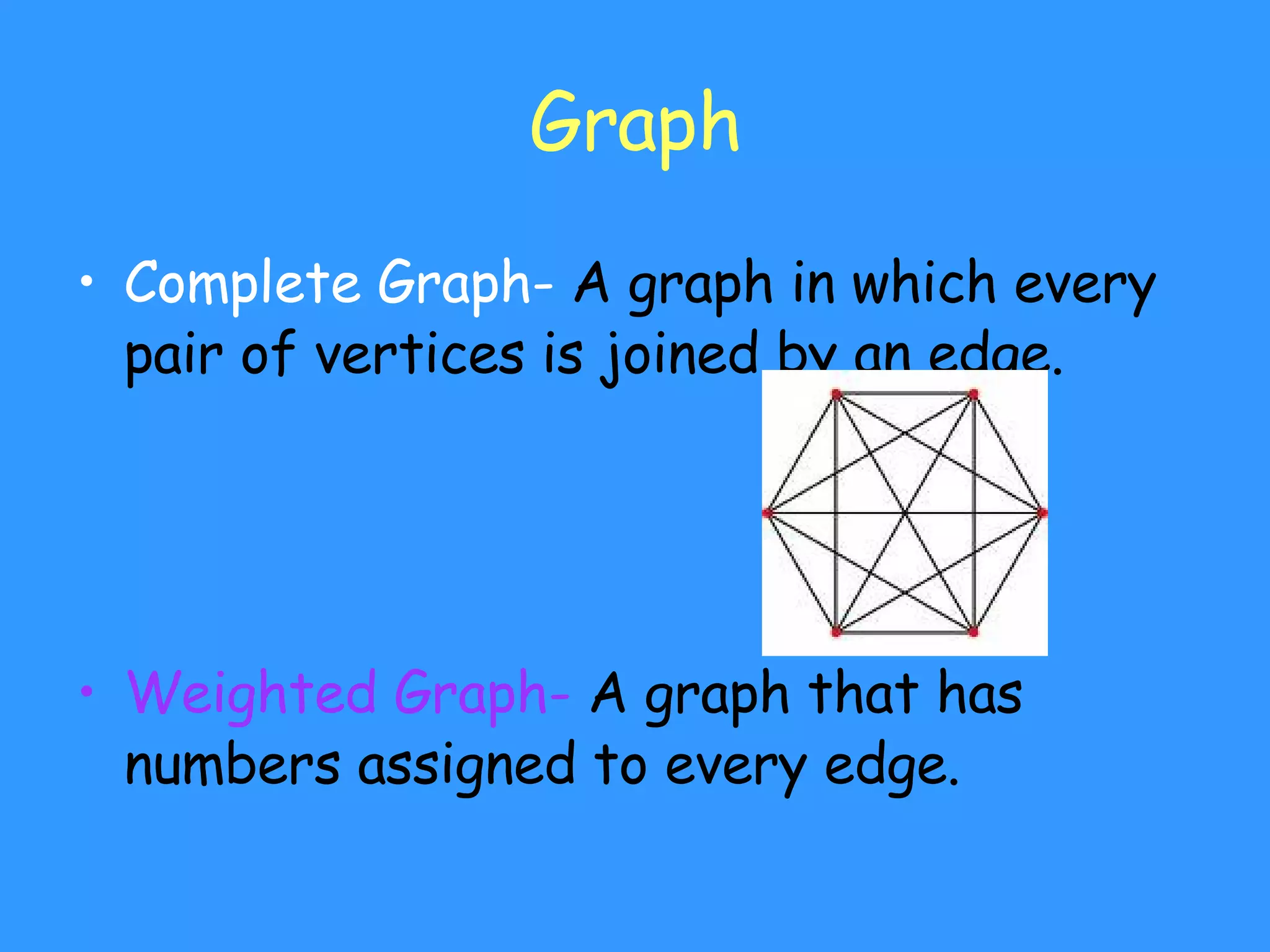
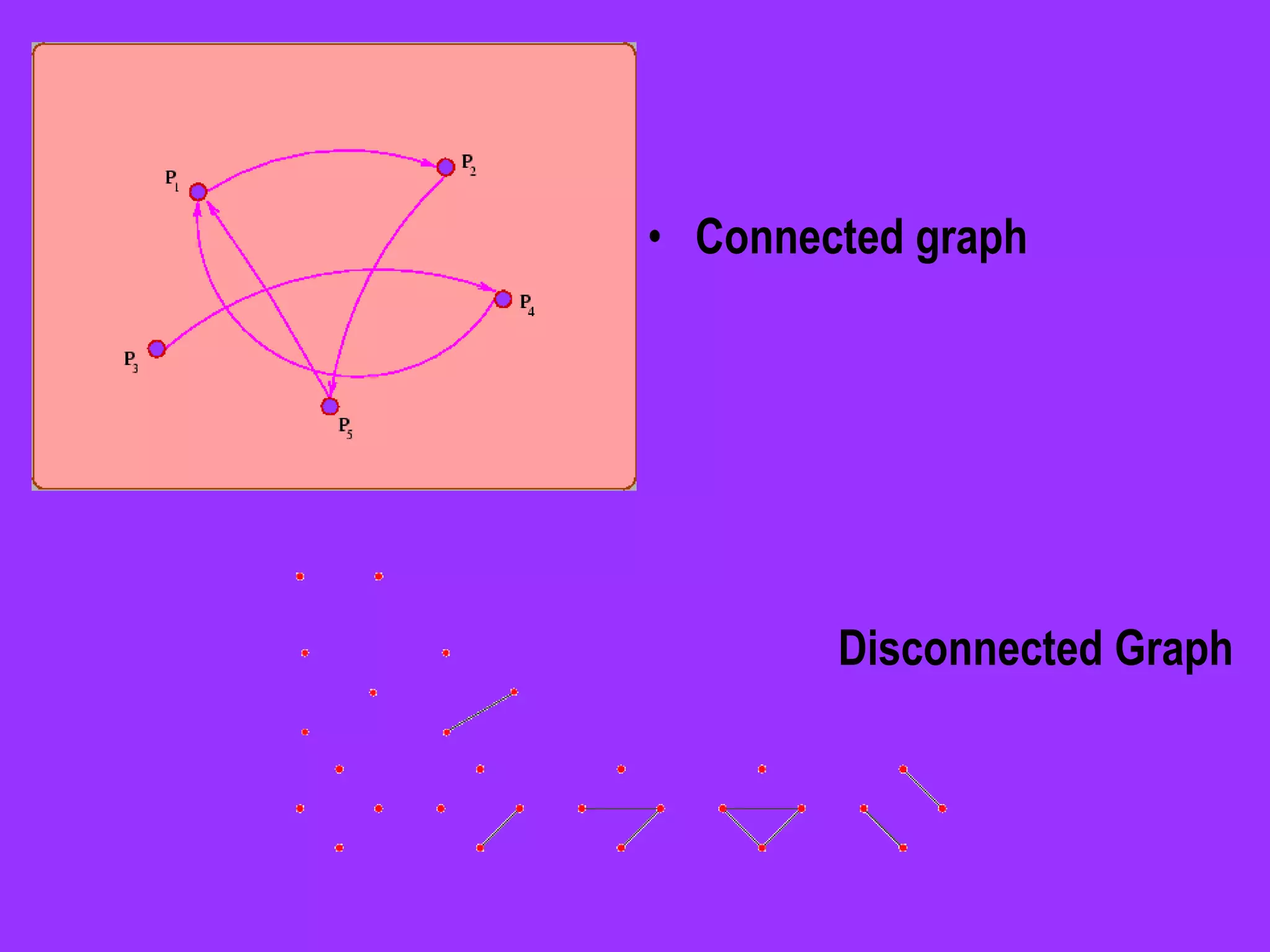
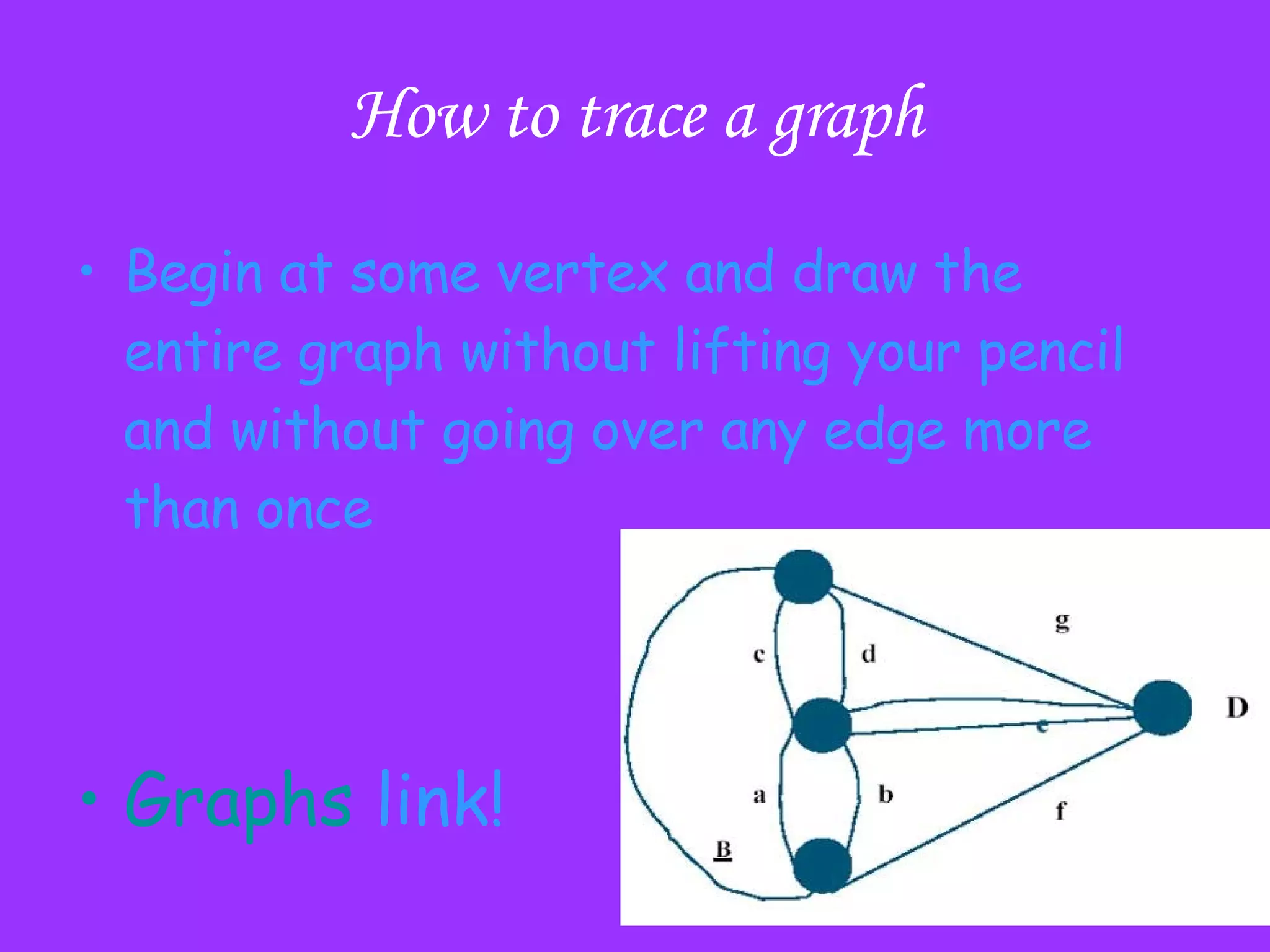
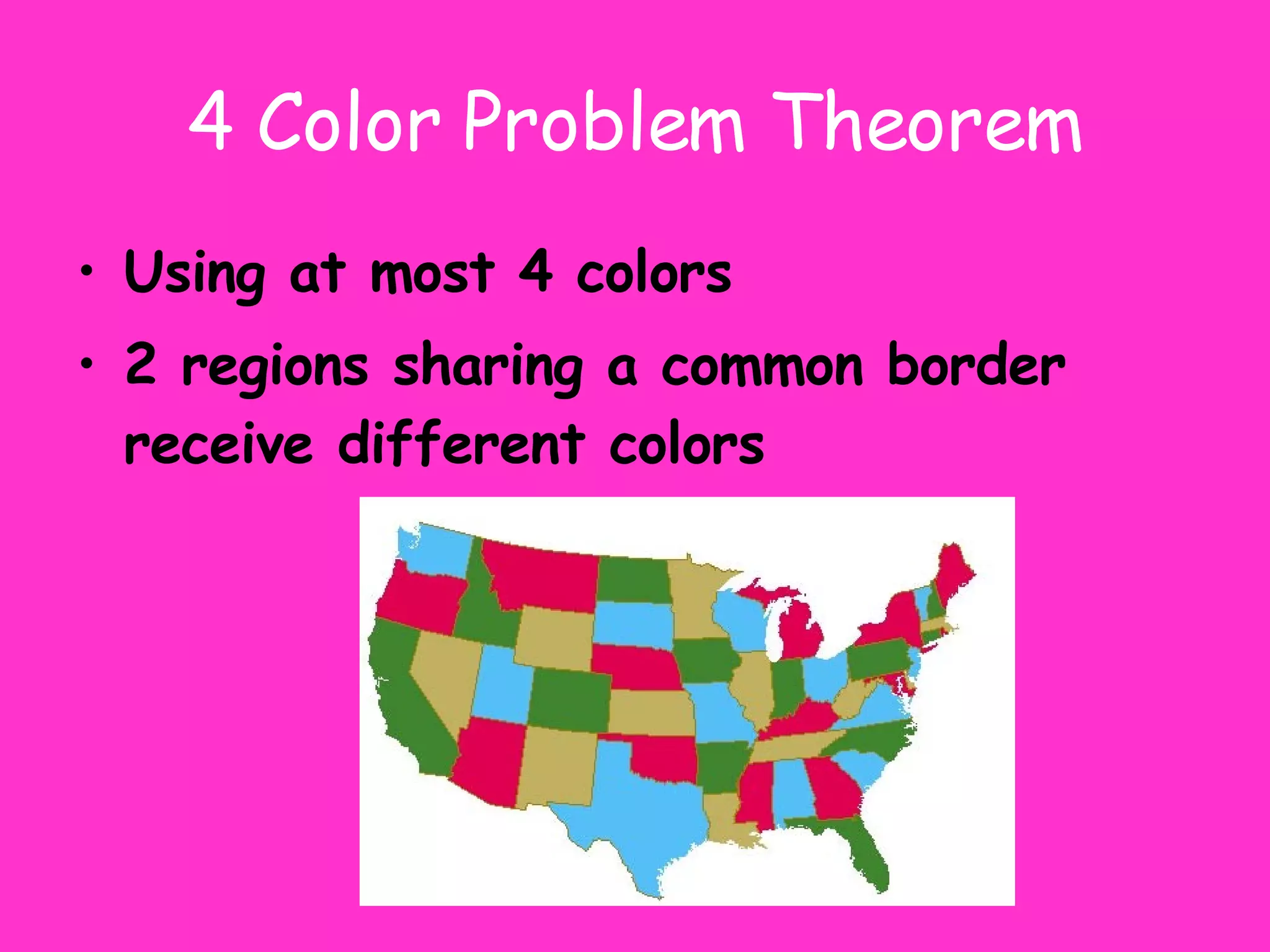
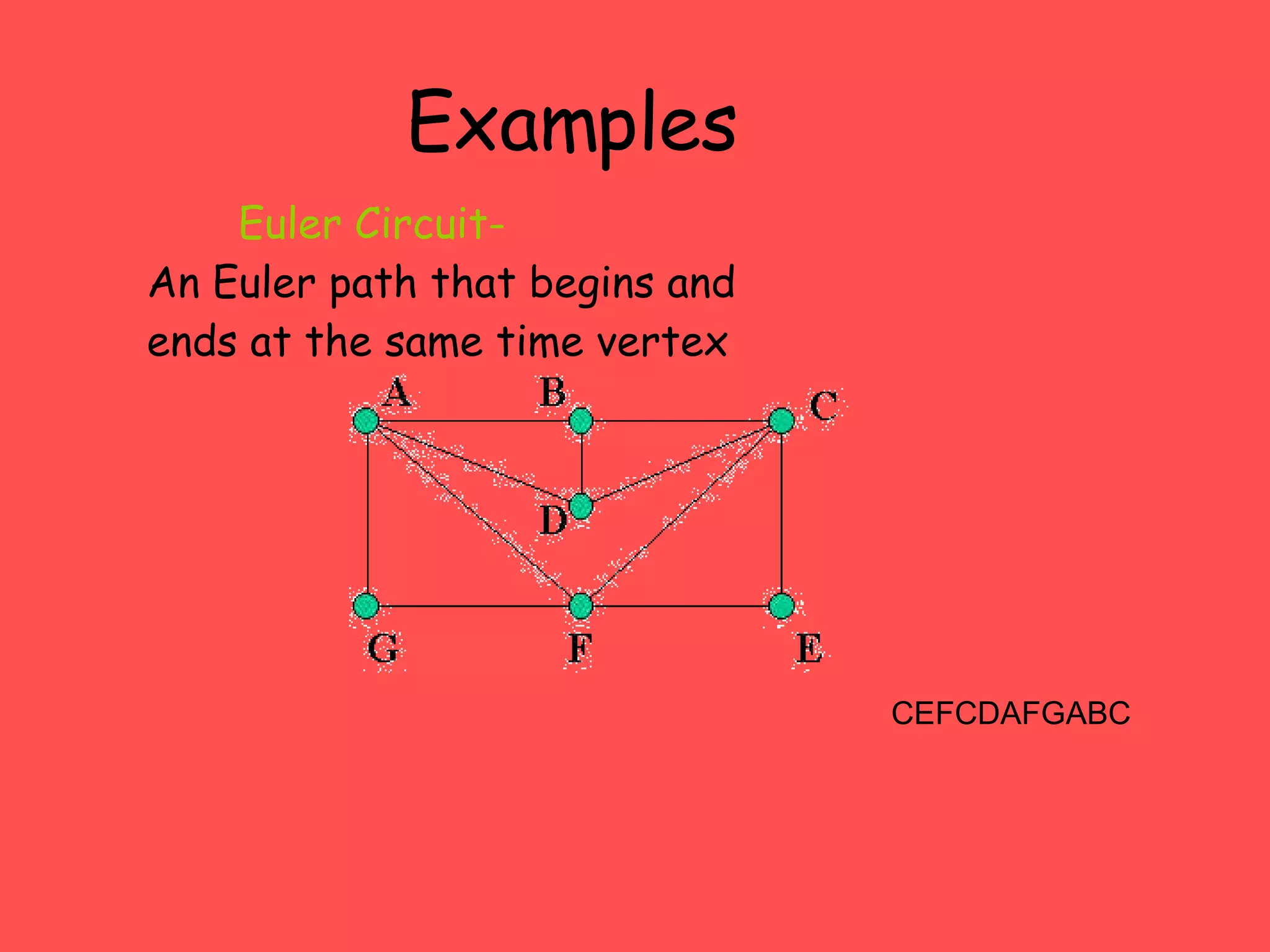
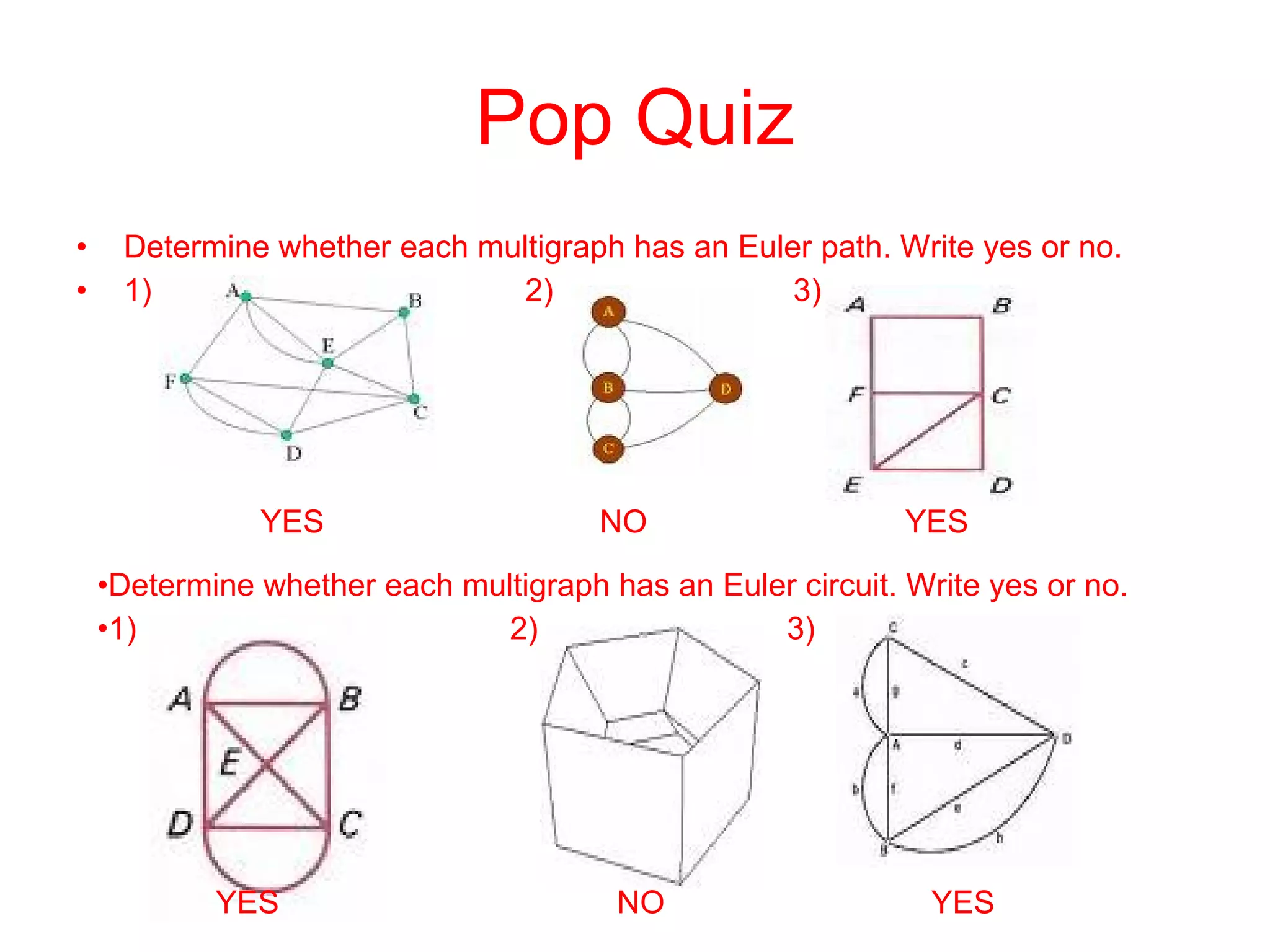
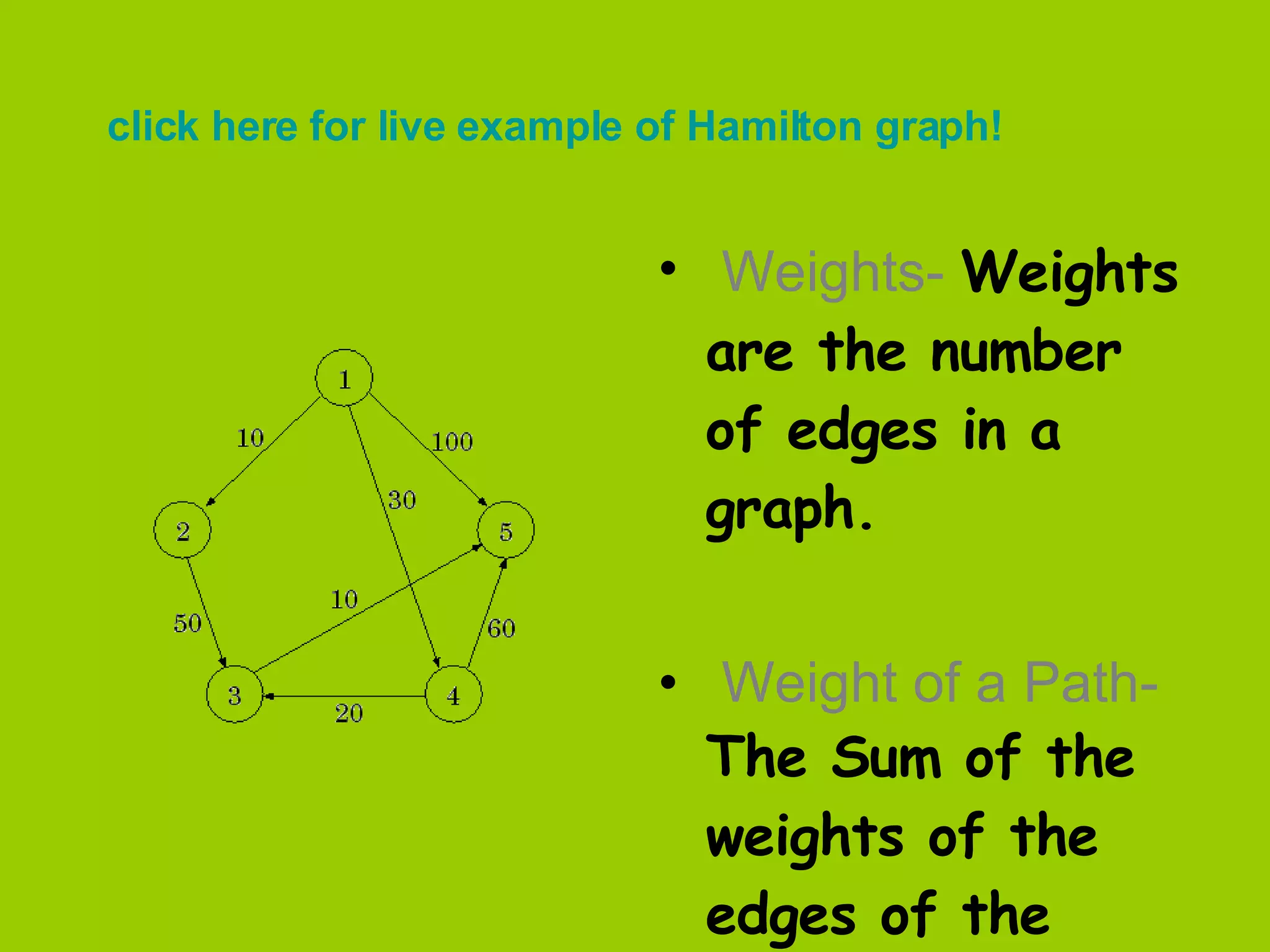
This document discusses key concepts in graph theory including: - Graphs consist of vertices connected by edges - Connected graphs allow travel between all vertices via edges - Bridges, if removed, disconnect a graph - The four color theorem states regions sharing a border need different colors - Euler's theorem provides conditions for when a graph can be traced using each edge once - Hamilton paths pass through each vertex once while circuits begin and end at the same vertex

1. Graph Theory Chapter 3 By: Amber Dejha Sahar Isiah Kamal

2. 3.1 Graphs, Puzzles, and Map Coloring

3. Graphs Graph- consist of finite set of point called vertices and lines called edges, that join pairs of vertices Connected graph- if it is possible to travel from any vertex to any other vertex of the graph by moving along successive edges Bridge- connected graph is an edge such that if it were removed the graph is no longer connected

4. Connected graph Disconnected Graph

5. How to trace a graph Begin at some vertex and draw the entire graph without lifting your pencil and without going over any edge more than once Graphs link!

6. 4 Color Problem Theorem Using at most 4 colors 2 regions sharing a common border receive different colors

7. 3.2 Hamilton & Circuit Paths

8. Euler Theorem A graph can be traced if……. It is connected It has either no odd vertices or two odd vertices If it has 2 odd vertices, the tracing must begin at one of these and end at the other. If all the vertices are even, then the tracing must begin and end at the same vertex .

9. Euler Path- A path in a graph is a series of consecutive edges in which no edge is repeated. The number in a path is called its length. Euler Path- A path containing all the edges of a graph.(tracing)

10. Examples CEFCDAFGABC Euler Circuit- An Euler path that begins and ends at the same time vertex

11. Eulerian Graph- A graph with all even vertices. Eulerizing A Graph- Duplicate some edges in a graph to make all the vertices even . Euler Graph

12. Hamilton Path Hamilton Path- A path that passes through all the vertices of a graph exactly once is called a Hamilton Path. Hamilton Circuit- A Hamilton Path that begins and ends at the same vertex .

13. Graph Complete Graph- A graph in which every pair of vertices is joined by an edge. Weighted Graph- A graph that has numbers assigned to every edge.

14. Weights- Weights are the number of edges in a graph. Weight of a Path- The Sum of the weights of the edges of the path. click here for live example of Hamilton graph!

15. Pop Quiz Determine whether each multigraph has an Euler path. Write yes or no. 1) 2) 3) Determine whether each multigraph has an Euler circuit. Write yes or no. 1) 2) 3) YES NO YES YES NO YES