Educational

1. Discrete Mathematics
GRAPH THEORY

2. 1. Assignment of jobs to employees of an organization
2. The outcomes of round-robin tournaments.
3. To model acquaintanceship between people
4. Telephone calls between telephone numbers, and links between
websites.
5. To walk down all the streets in a city without going down a street
twice
6. Circuit board.
7. Two chemical compounds with the same molecular formula but
different structures using graphs.
8. Computer networks.
Graph Theory Application

3. WHAT IS GRAPH THEORY?
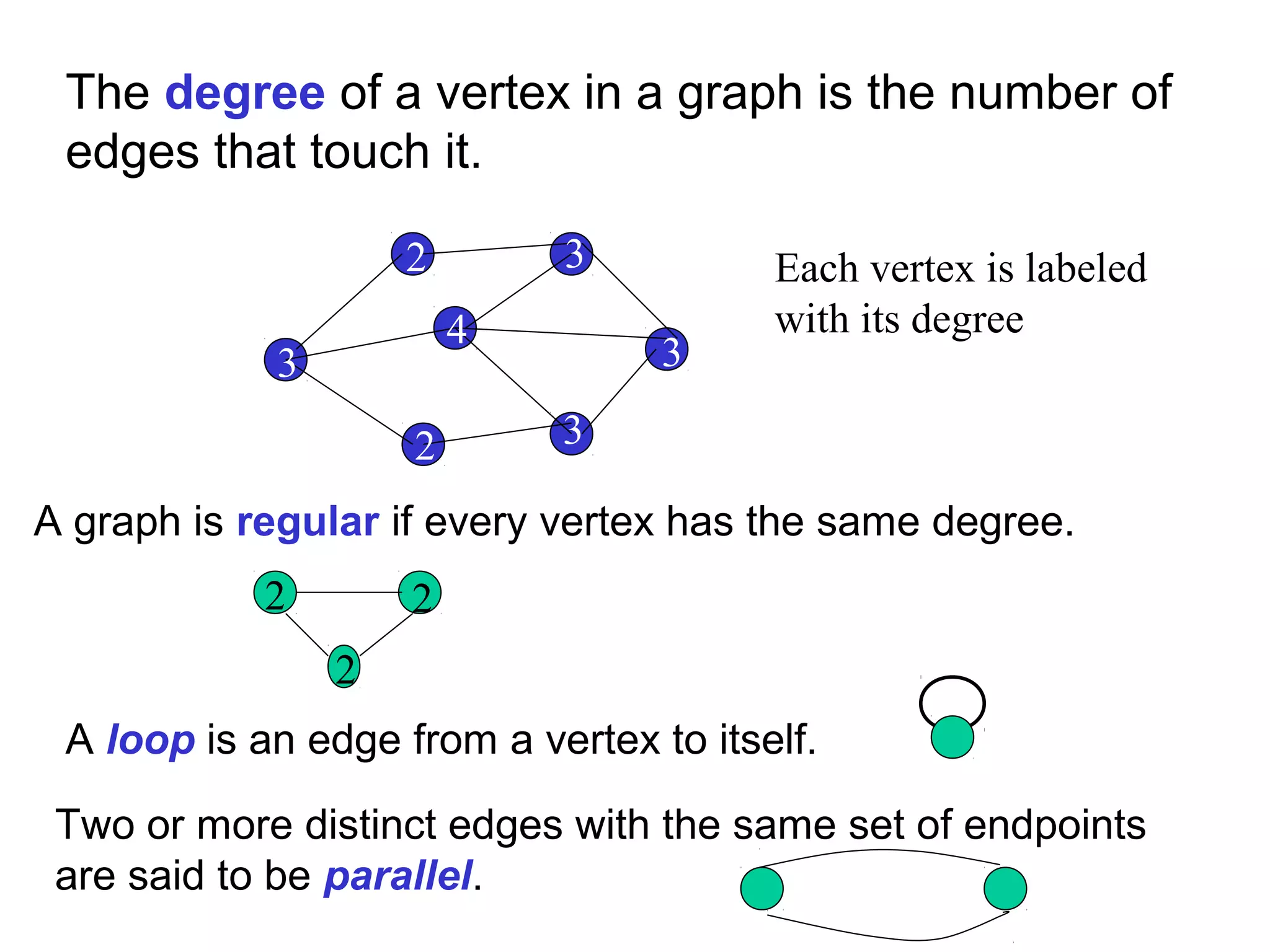
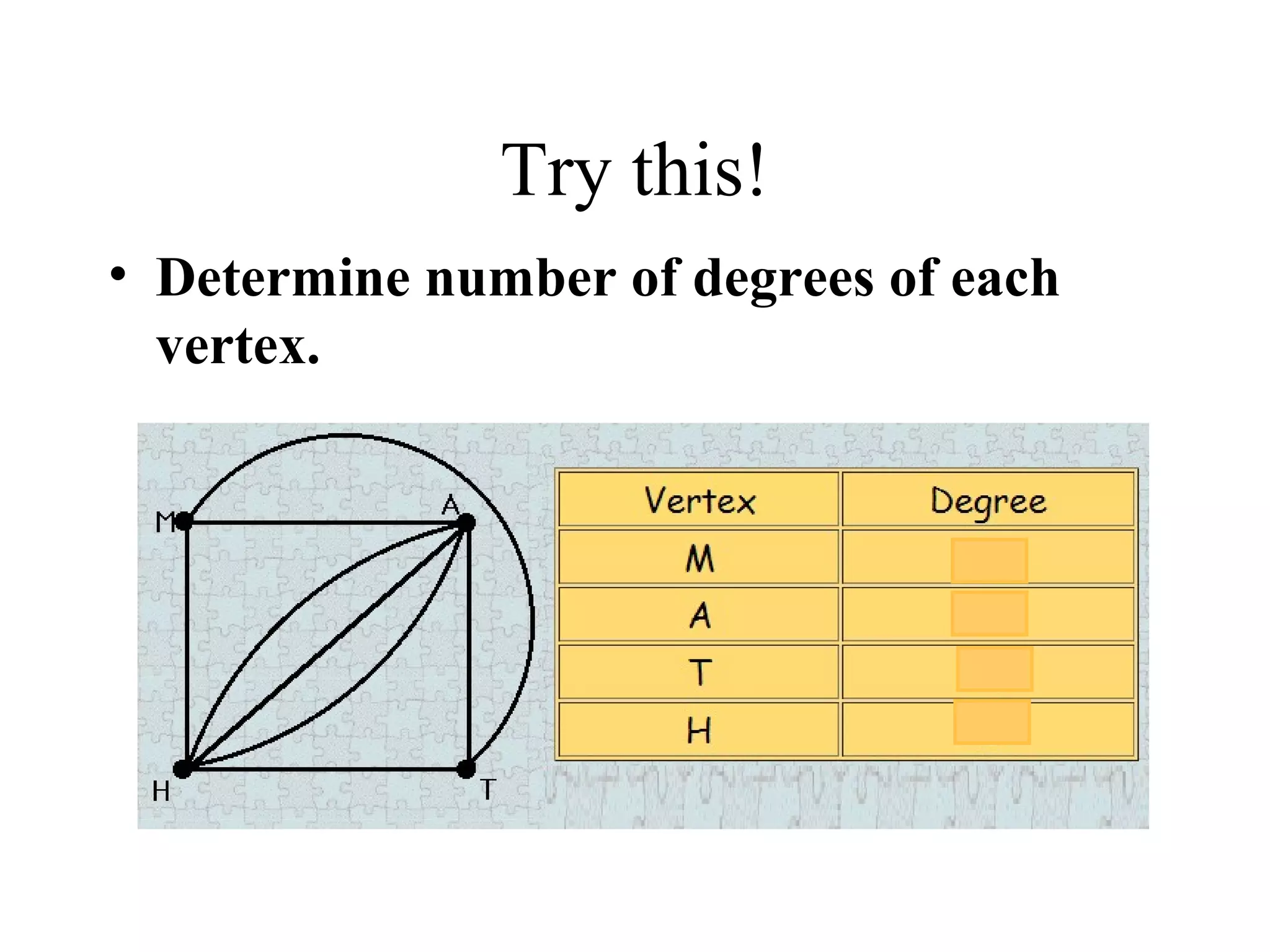
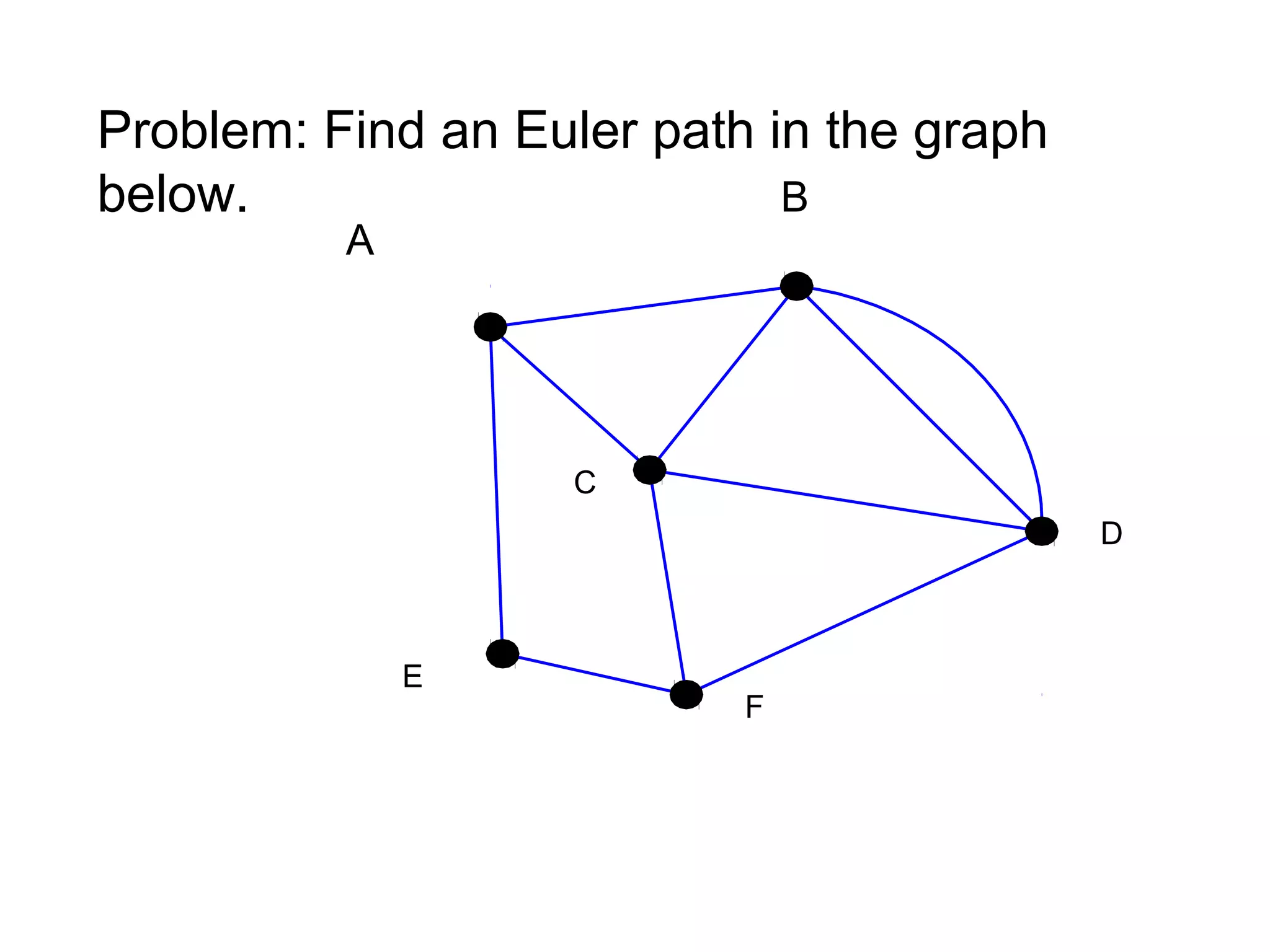
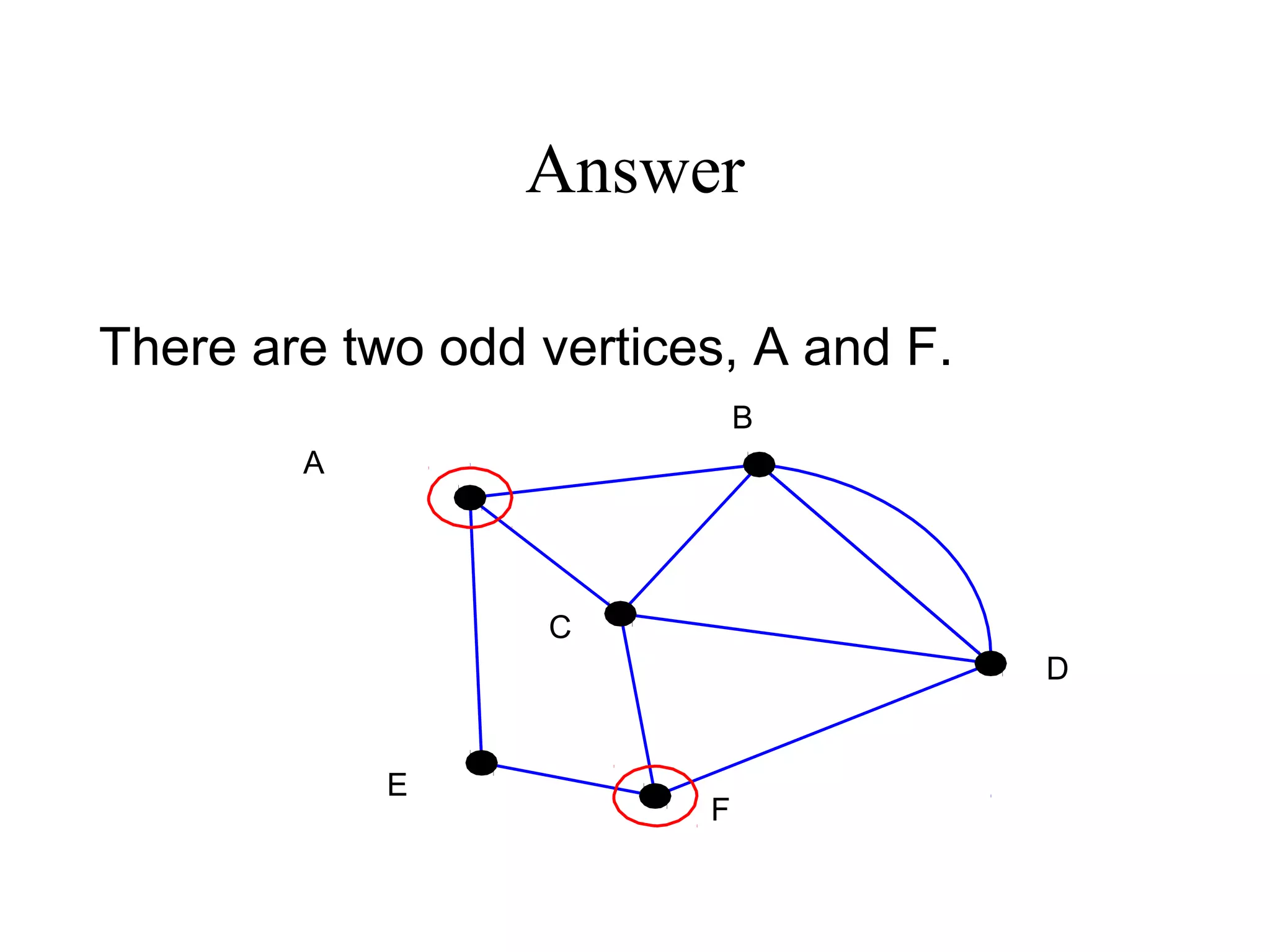
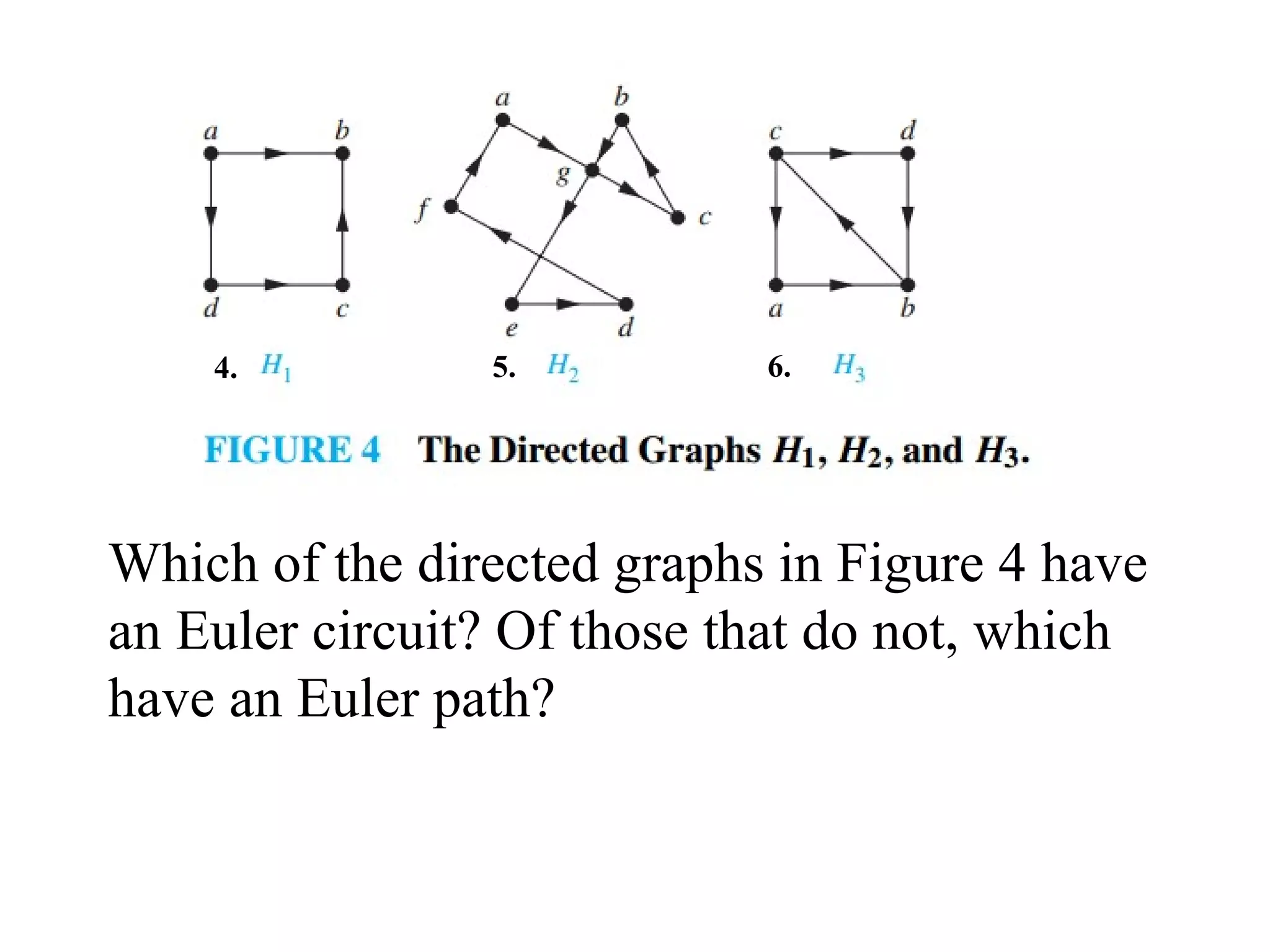
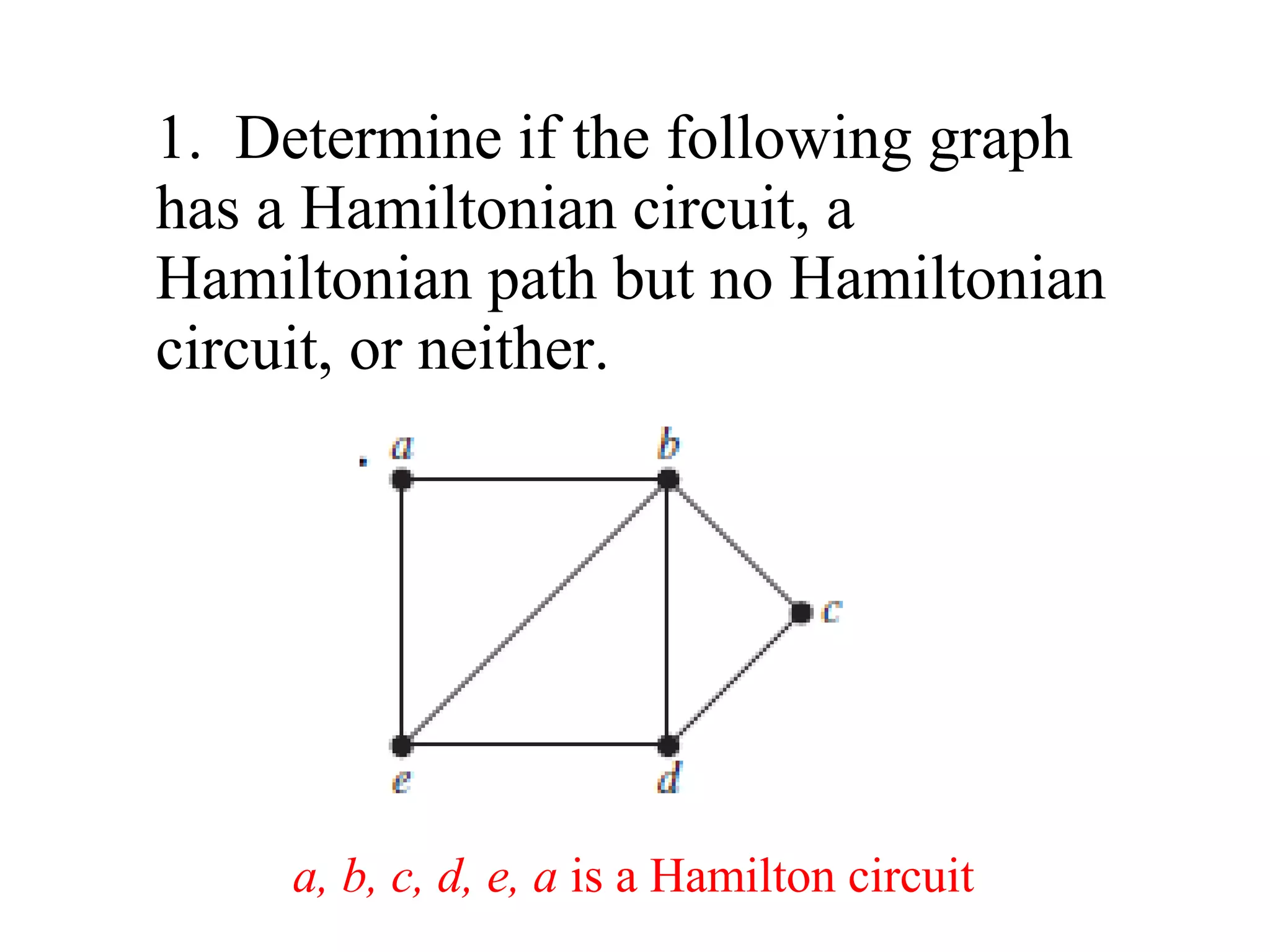
• Graph theory is the study of mathematical
structures called graphs that are used to model
pairwise relations between objects from a
certain collection.
• The origin of graph theory can be traced back
to Leonard Euler's (German pronounciation ley-
awn-hahrt OY-lər) work on the “Konigsberg
bridge problem” on 1736.

4. Königsberg
City in Germany

5. THE Bridges of the Konigsberg
• The question is whether a person can plan a walk in
such a way that he will cross each of these bridges
once but not more than once.
This can be pictured as follows:
A
B
C
D
e1
e5
e2
e6
e4
e7
The vertices are V={A,B,C,D} and the edges are E =
{e1,e2,e3,e4,e,5,e6,e7}. e1 and e2 is associated with the unordered
pair (A,B), e5 and e6 is associated with (B,C), e3 is associated
with (B,D), e4 and e7 is associated with (A,D) and so on.
e3

6. Definition
A graph G = (V ,E) consists of V , a nonempty
set of vertices (or nodes) and E, a set of edges.
Each edge has either one or two vertices associated
with it, called its endpoints. An edge is said to
connect its endpoints.

7. Vertex Edge Graph
Vertex Edge Graph - A collection of points
some of which are joined by line segments
or curves.
This graph has 6 vertices and 7 edges
Each point is a vertex and each line is an edge

8. Example:
Let V ={1, 2, 3, 4}, and E={e1, e2, e3, e4, e5}.
Let γ be defined by e1=e5={1, 2}, e2={4, 3},
e3={1, 3}, e4={2, 4}.
Draw, G={V, E}

9. e1
e5
e2
e3
e4
e1
e5
e2
e3
e4
e1
e5
e2
e3
e4

10. The degree of a vertex in a graph is the number of
edges that touch it.
3
2
2
4
3
3
3 Each vertex is labeled
with its degree
A graph is regular if every vertex has the same degree.
2
2
2
A loop is an edge from a vertex to itself.
Two or more distinct edges with the same set of endpoints
are said to be parallel.

11. The degree of a vertex is not the same as the number of
edges that are incident with U since any loop in U is
counted twice.

12. An isolated vertex is a vertex of degree 0.
A vertex U is incident with an edge e, if e is either a loop at U or
it has the from e={u,v}.

13. Try this!
• Determine number of degrees of each
vertex.

14. Seatwork: Find the degree of each vertex.
Vertices Degree
A
B
C
D
E
Vertices Degree
A
B
C
D
E
1. 2.

15. 3.
Vertices Degree
A
B
C
D
E

16. BASIC CONCEPTS
Let U and W be vertices of a graph G.
•A walk from U to W is an alternating sequence of
vertices and edges of G, beginning with the vertex U
and ending in the vertex W, with the property that
each edge is incident with the vertex immediately
preceding it and the vertex immediately following it
in the sequence.
•A walk that begins and ends at the same vertex is
called a closed walk. On the other hand, a walk that
begins and ends at two different vertices is called an
open walk.

17. BASIC CONCEPTS
• The complete graph of order n, denoted by Kn is the
graph that has n vertices and exactly one edge
connecting each of the possible pairs of distinct vertices.
• A graph H is called a subgraph of a graph G if every
vertex of H is also a vertex of G and every edge of H is
also an edge of G.
• A path in a graph is a sequence: v1, v2, v3, . . . vk, such
that it is possible to travel from v1 to vk without using the
same edge twice .
• A circuit is a path that begins and ends at the same
vertex.

18. Complete Graph

19. SUBGRAPH

20. Complete
Graph
Subgraphs:

21. An Eulerian path in a graph is a path that travels
along every edge of the graph exactly once. An
Eulerian path might pass through individual
vertices of the graph more than once.
Euler Graph (pronounced oilier)
Start and finish
Euler circuits is a path that ends at the same vertex it started
A Euler path is a
snowplow problem
where a snow plow
needs to plow every
street once.

22. QUIZ (1/4)
1. Two edges are said to be adjacent if they share
a common________.
2. The ________of a vertex U is number of times
an edge meets U.
3. The graph that has n vertices and exactly one
edge connecting each of the possible pairs of
distinct vertices.
4. A walk that begins and ends at the same vertex
is called a/an__________.
5. Two or more distinct edges with the same
set of endpoints are called _______.

23. SEATWORK:
For Items # 1 to # 3, consider the graph:
1. Identify the elements of V and
E.
2. List down the functions γ(e)
for all e.
3. Give the degree of each
vertex.
4. Draw the graph G = {V, E, γ}, where V={A, B, C, D,
E}, E ={e1, e2, e3, e4, e5, e6} , γ(e1)=γ(e5)={A, C} ,
γ(e2)={A, D}, γ(e3)={E, C}, γ(e4)={B, C}, and
γ(e6)={E, D}

24. THEORIES ABOUT EULER CIRCUITS
• A connected multigraph with at least
two vertices has an Euler circuit if and
only if each of its vertices has even
degree.

25. THEORIES ABOUT EULER PATHS
• A connected multigraph has an Euler
path but not an Euler circuit if and only
if it has exactly two vertices of odd
degree.

26. Draw the Vertex/edge graph and answer the following questions.
1) How many vertices are there?
2) How many edges are there?
3)How many vertices have a degree of 2?
4) How many vertices have a degree of 4?
Draw a Euler circuit starting at the vertex with a white dot.
Remember: A circuit travels along every path exactly once and
may pass through vertices multiple times before ending at the
starting vertex.
6
9
3
3

27. # of ODD Vertices Implication (for a connected graph)
0
There is at least
one Euler Circuit.
1 THIS IS IMPOSSIBLE! Can’t be drawn
2
There is no Euler Circuit
but at least 1 Euler Path.
more than 2
There are no Euler Circuits
or Euler Paths.
Use this chart to see if a Euler path or circuit may be drawn

28. Problem: Find an Euler path in the graph
below. B
A
F
E
D
C

29. Answer
There are two odd vertices, A and F.
B
A
F
E
D
C

30. Which of the following have an Euler
circuit, an Euler path but not a Euler
circuit, or neither?
Neither: NO EP, NO EC EP BUT NOT EC

31. Which of the following have an Euler
circuit, an Euler path but not a Euler
circuit, or neither?
NO EP, BUT EC

32. Quiz
Which of the undirected graphs in Figure 3
have an Euler circuit? Of those that do not,
which have an Euler path?
1. 2. 3.

33. Which of the directed graphs in Figure 4 have
an Euler circuit? Of those that do not, which
have an Euler path?
4. 5. 6.

34. Sir William Rowan Hamilton
• In the 19th
century, an Irishman named Sir
William Rowan Hamilton (1805-1865)
invented a game called the Icosian game.
• The game consisted of a graph in which the
vertices represented major cities in Europe.

35. Hamiltonian Circuit/Paths:
A Hamiltonian path in a graph is a path that
passes through every vertex in the graph exactly
once. A Hamiltonian path does not necessarily
pass through all the edges of the graph, however.
A Hamiltonian path which ends in the same place in
which it began is called a Hamiltonian circuit.

36. Example
• Which of the simple graphs have a Hamilton
circuit or, if not, a Hamilton path, or neither?
Solution:
G1 Hamilton circuit: a, b, c, d, e, a.
G2 There is no Hamilton circuit, but G2 does have a Hamilton path, namely,
a, b, c, d.
G3 has neither a Hamilton circuit nor a Hamilton path, because any path
containing all vertices must contain one of the edges {a, b}, {e, f}, and {c, d}
more than once.

37. Examples
Hamiltonian
path: a, b, c, d, e
Hamiltonian circuit: A,
D, C, B, A

38. Trace a Hamiltonian path
Only a path, not a circuit. The path did
not end at the same vertex it started.
The path does not need to go over every edge but it can only go
over an edge once and must pass through every vertex exactly
once.
Hamiltonian Circuits
are often called the
mail man circuit
because the mailman
goes to every mailbox
but does not need to go
over every street.

39. 1. Determine if the following graph
has a Hamiltonian circuit, a
Hamiltonian path but no Hamiltonian
circuit, or neither.
a, b, c, d, e, a is a Hamilton circuit

40. 2. Does the graph have a Hamilton path? Ifso, find such a
path. If it does not, give an argument to show why no
such path exists.
a, b, c, f, d, e is a Hamilton path

41. 3. Does the graph in Exercise 32 have a Hamilton path? If
so, find such a path. If it does not, give an argument to
show why no such path exists.
f, e, d, a, b, c is a Hamilton path.

42. Review:
Euler Graphs Passes over edge exactly once. May pass
through a vertex more than once.
Hamiltonian
Graphs
Passes through every vertex exactly once but
not necessarily over every edge.
Circuits The path ends at the same vertex it started.

43. Quiz Answer
1. VERTEX
2. DEGREE
3. COMPLETE GRAPH
4. CLOSE WALK
5. PARALLEL

44. Quiz Answer
Solution:
1. G1 has an Euler circuit, a, e, c, d, e, b, a.
2. G2 Neither
3. G3 has an Euler path, namely, a, c, d, e, b, d, a, b.
4. H1 Neither
5. H2 has an Euler circuit, a, g, c, b, g, e, d, f, a
6. H3 has an Euler path, namely, c, a, b, c, d, b