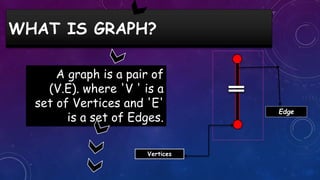
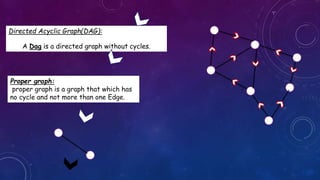
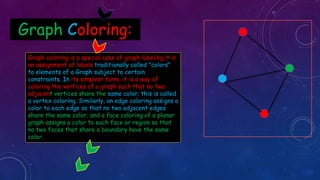
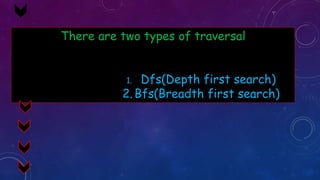
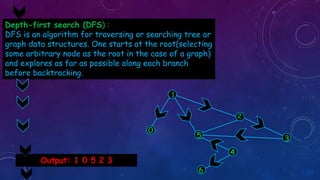
The document provides an overview of graph concepts including definitions of a graph as a pair of vertices and edges, different types of graphs such as directed/undirected graphs and cyclic/acyclic graphs. It also discusses graph coloring, adjacency matrices/lists for representing graphs, and algorithms for traversing graphs including depth-first search and breadth-first search. Examples are given for each concept to illustrate key differences and properties.

1. PRESENTATION
ABOUT:
GRAPH

2. Contents For Our
Presentation...
1. what is Graph,vertices and Edge?
2. kinds of Graph.
3. Graph Coloring.
4. Adjacent Matrix.
5. Adjacent List .
6. Depth First search.
7. Breath First search.

3. WHAT IS GRAPH?
A graph is a pair of
(V.E). where 'V ' is a
set of Vertices and 'E'
is a set of Edges.
Vertices
Edge

4. kinds of Graph:
Undirected Graph:
In an undirected graph, the order of the
vertices in the pairs in the Edge set
doesn't matter
Directed Graph:
In a directed graph the order of the
vertices in the pairs in the edge set
matters.
Cyclic Graph:
A cyclic graph is a directed graph with at
least one cycle. A cycle is a path along the
directed edges from a vertex to itself. The
vertex labeled graph above as several
cycles.

5. Directed Acyclic Graph(DAG):
A Dag is a directed graph without cycles.
Proper graph:
proper graph is a graph that which has
no cycle and not more than one Edge.

6. Graph Coloring:
Graph coloring is a special case of graph labeling,it is
an assignment of labels traditionally called "colors"
to elements of a Graph subject to certain
constraints. In its simplest form, it is a way of
coloring the vertices of a graph such that no two
adjacent vertices share the same color; this is called
a vertex coloring. Similarly, an edge coloring assigns a
color to each edge so that no two adjacent edges
share the same color, and a face coloring of a planar
graph assigns a color to each face or region so that
no two faces that share a boundary have the same
color.

7. Adjacency Matrix:
Adjacency matrix:
A two-dimensional matrix, in which the rows
represent source vertices and columns represent
destination vertices. Data on edges and vertices
must be stored externally. Only the cost for one edge
can be stored between each pair of vertices.
A
D
E

8. Adjacency list:
Vertices are stored as records or objects, and every
vertex stores a list of adjacent vertices. This data
structure allows the storage of additional data on the
vertices. Additional data can be stored if edges are also
stored as objects, in which case each vertex stores its
incident edges and each edge stores its incident vertices.
For That Example Adjacency list Will be:
A->B->E->F->D
A->B->C->D
A->C->D

9. There are two types of traversal
1. Dfs(Depth first search)
2.Bfs(Breadth first search)

10. Depth-first search (DFS) :
DFS is an algorithm for traversing or searching tree or
graph data structures. One starts at the root(selecting
some arbitrary node as the root in the case of a graph)
and explores as far as possible along each branch
before backtracking.
1
0
6
Output: 1 0 5 2 3

11. Breadth-first search:
(BFS) is an algorithm for traversing or searching tree
or graph data structures. It starts at the tree rootand
explores the neighbor nodes first, before moving to the
next level neighbours.Compare BFS with the equivalent,
but more memory-efficient Interactive deeping depth
and contrast with depth-first search and contrast with
depth first search.
A
B
c E
F H
Queue Status
OUTPUT : A B S C G D E F H G
S

12. Thank you...!!!