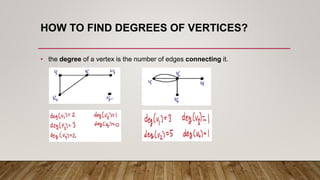
The document explains Euler paths and circuits, defining an Euler path as a path that uses every edge of a graph exactly once, while an Euler circuit returns to the starting vertex. It outlines the conditions for the existence of these paths and circuits, particularly concerning the degrees of vertices. Fleury's algorithm is presented as a method to find these paths or circuits based on vertex degree conditions and edge selection.

1. EULER PATHS AND
CIRCUITS
BY M PIR SYED AYAZ FARID SHAH
CLASS MCS 4TH

2. HOW TO FIND DEGREES OF VERTICES?
• the degree of a vertex is the number of edges connecting it.

3. EULER PATHS AND CIRCUITS
• An Euler path is a path that uses every edge of a graph exactly once. An Euler
path starts and ends at deferent vertices.
• An Euler circuit is a circuit that uses every edge of a graph exactly once. An Euler
circuit starts and ends at the same vertex.
• Our goal is to find a quick way to check whether a graph (or multigraph) has an Euler path or
circuit.

4. EULER PATHS AND CIRCUITS
• If a graph G has an Euler path,
then it must have
• exactly two odd vertices.
• If a graph G has an Euler circuit,
then all of its vertices
• must be even vertices.

5. FLEURY'S ALGORITHM
• To find an Euler path or an Euler circuit:
• 1. Make sure the graph has either 0 or 2 odd vertices.
• 2. If there are 0 odd vertices, start anywhere. If there are 2
• odd vertices, start at one of them.
• 3. Follow edges one at a time. If you have a choice between
• a bridge and a non-bridge, always choose the non-bridge.
• 4. Stop when you run out of edges.
• This is called Fleury's algorithm, and it always works!