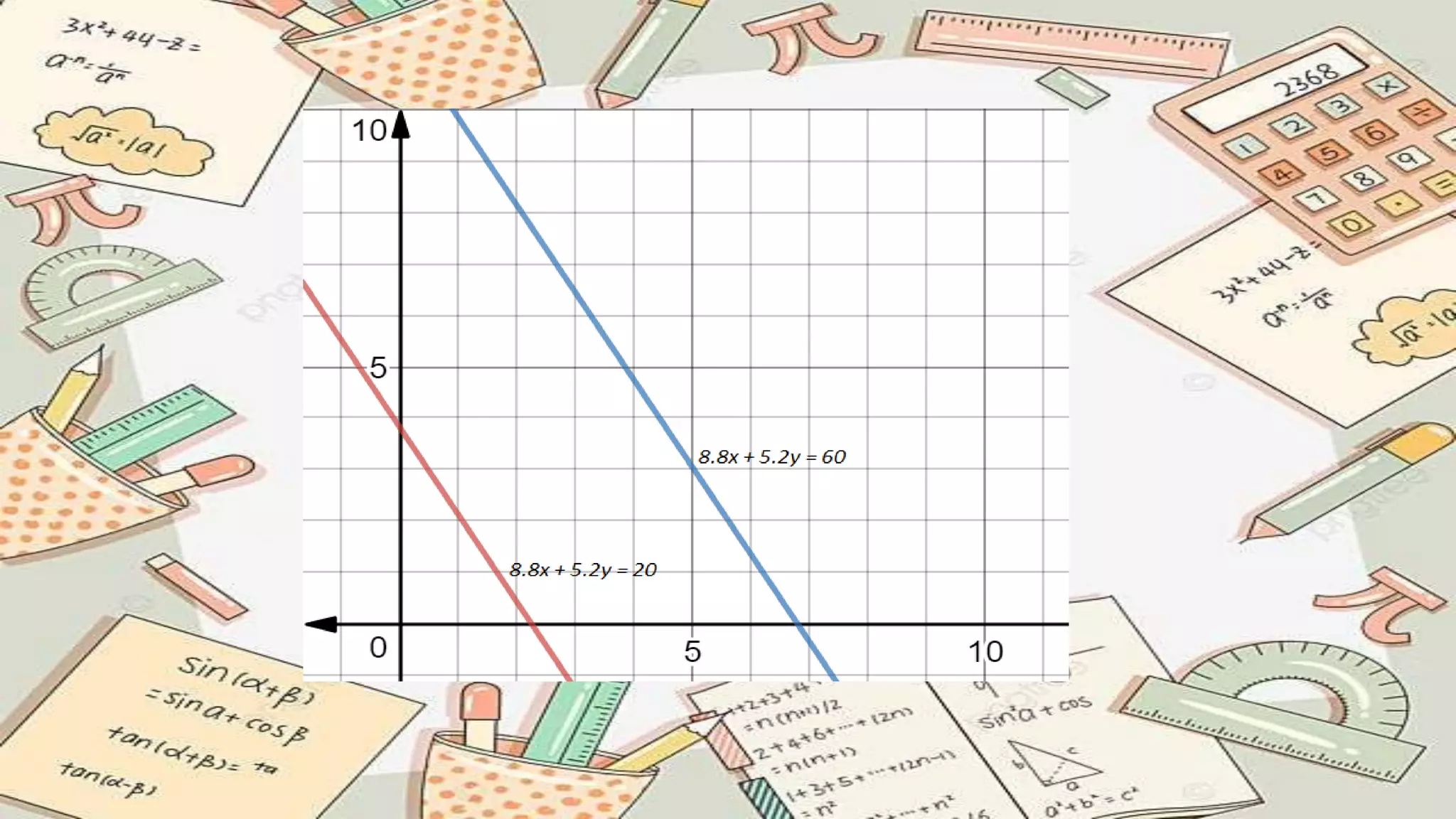
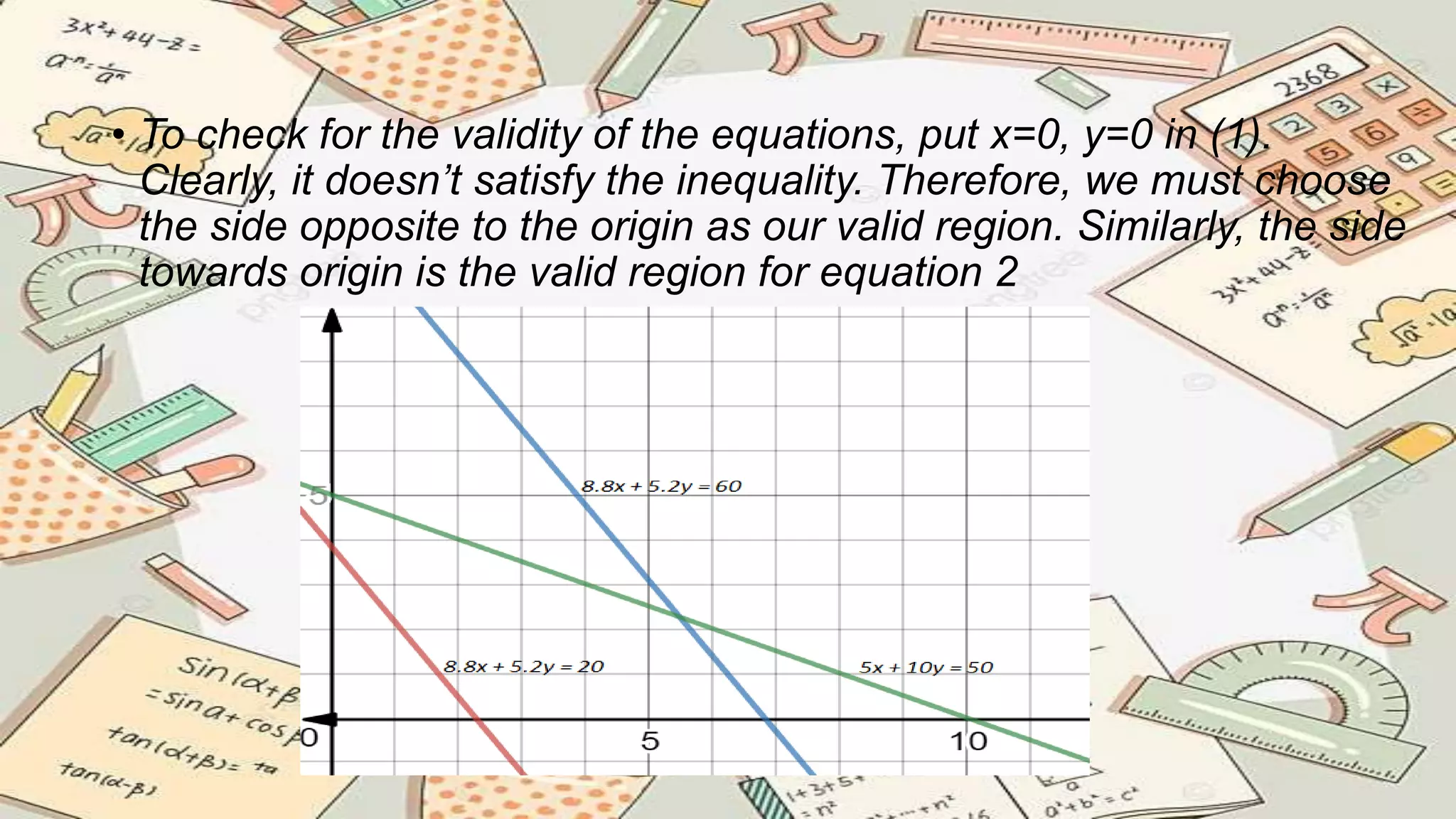
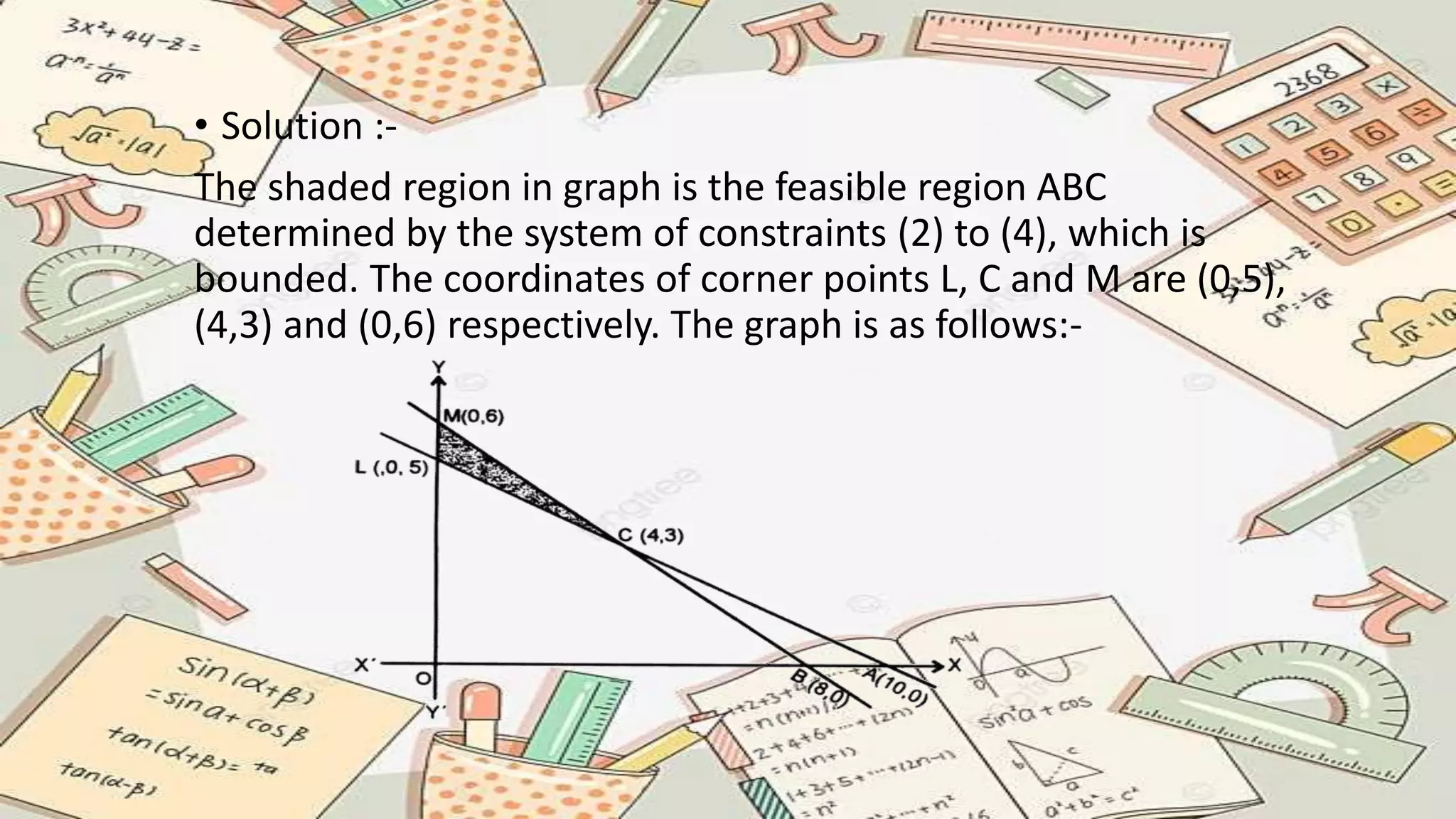
Linear programming is a process used to optimize a linear objective function subject to linear constraints. It can be applied to problems in manufacturing, diets, transportation, allocation and more. Key components include decision variables, constraints, and an objective function. The process involves formulating the problem, identifying variables and constraints, solving using graphical or simplex methods, and interpreting the optimal solution. Linear programming provides a tool for modeling real-world problems mathematically and determining the best outcome.

1. LINEAR PROGRAMMING
PROBLEMS
• Linear programming problems also
long for LPP is a problem that is
concerned with finding the optimal
value of the given
• linear function.
• The optimal value can be either
maximum value or the minimum
value. Here the given linear function
is known as objective linear function.

2. • The linear programming problem can be used to get optimal
solution for the following scenarios such as :-
1) Manufacturing problems
2) Diet problems
3) Transportation problems
4) Allocation problems
There are some components of linear programming these are :-
1) Decision variables
2) constraints
3) Data
4) Objective Function

3. What is Linear Programming ?
• Linear programming is a process that is used
to determine the best outcome of a linear
function. It is the best method to perform linear
optimisation by making a few simple
assumptions
• The linear function is also called the objective
function.
• It is also used as a method to depict a
complicated real world relationship by using
the elements in the mathematical form.

4. APPLICATION OF LPP IN FOOD
& AGGRICULTURE
• Farmers apply linear programming techniques to their work.
By determining what crops they should grow, the quantity of
it and how to use it efficiently, farmers can increase their
revenue.
• In nutrition, linear programming provides a powerful tool to
aid in planning for dietary needs. In order to provide healthy,
low-cost food baskets for needy families, nutritionists can
use linear programming. Constraints may include dietary
guidelines, nutrient guidance, cultural acceptability or some
combination thereof.

5. APPLICATION OF LPP IN
ENGINEERING
• Engineers also use linear programming to help solve design
and manufacturing problems. For example, in airfoil meshes,
engineers seek aerodynamic shape optimization. This allows
for the reduction of the drag coefficient of the airfoil.
• Constraints may include lift coefficient, relative maximum
thickness, nose radius and trailing edge angle. Shape
optimization seeks to make a shock-free airfoil with a
feasible shape. Linear programming therefore provides
engineers with an essential tool in shape optimization.

6. FORMULAS
• A linear programming problem will consist of decision
variables, an objective function, constraints and non
negative restrictions. The constraints are the restrictions
that are imposed on the decision variables to limit their
value.
• The decision variables must always have a non negative
value which is given by the non negative restrictions.
• The general formula of a linear function is:-
Z = ax + by
where Z is objective function

7. CONSTRAINTS
1) cx + dy ≤ e
2) E + qy ≤ h
THE INEQUALITIES CAN ALSO BE “≤ ”
NON NEGATIVE RESTRICTIONS
1)X≥0
2)Y≥0

8. HOW TO SOLVE ?
• The most important part of solving the linear programming
problem is to first formulate the problem using given
data and then use the following steps :-
1) Identify the decision variables
2) Formulate the objective function
3) Write down the constraints
4) Ensure the decision variables are greater than or less than 0
5) Solve the linear problem using the simple or graphical method

9. GRAPHICAL METHOD
• EXAMPLE :- A health-conscious family wants to
have a very well controlled vitamin C-rich mixed
fruit-breakfast which is a good source of dietary
fibre as well; in the form of 5 fruit servings per
day. They choose apples and bananas as their
target fruits, which can be purchased from an
online vendor in bulk at a reasonable price
Bananas cost 30 rupees per dozen and apples
cost 80 rupees per kg Every person of the
family would like to have at least 20 mg of
Vitamin C daily but would like to keep the intake
under 60 mg. How much fruit servings would the
family have to consume on a daily basis per
person to minimize their cost?

10. • ANS) ‘x’ = number of banana servings taken and
• ‘y’ = number of servings of apples taken.
• Cost of a banana serving = 30/6 rupees = 5 rupees.
Thus, the cost of ‘x’ banana servings = 5x rupees
• Cost of an apple serving = 80/8 rupees = 10 rupees.
Thus the cost of ‘y’ apple servings = 10y rupees
• Total Cost C = 5x + 10y
• Total Vitamin C intake:
8.8x + 5.2y ≥ 20 (1)
8.8x + 5.2y ≤ 60 (2)
• NOW LET US PLOT A GRAPH

12. • To check for the validity of the equations, put x=0, y=0 in (1).
Clearly, it doesn’t satisfy the inequality. Therefore, we must choose
the side opposite to the origin as our valid region. Similarly, the side
towards origin is the valid region for equation 2

13. • Now we must calculate the coordinates of
this point. To do this, just solve the
simultaneous pair of linear equations:
• y = 0
8.8x + 5.2y = 20
• We’ll get the coordinates of ‘P’ as (2.27, 0).
This implies that the family must consume
2.27 bananas and 0 apples to minimize their
cost and function according to their diet plan.

14. SIMPLE METHOD
• Example 2 Solve the following linear programming
problem graphically: Minimise Z = 200 x + 500 y ...
• subject to the constraints: x + 2y ≥ 10
3x + 4y ≤ 24
x ≥ 0,
y ≥ 0

15. • Solution :-
The shaded region in graph is the feasible region ABC
determined by the system of constraints (2) to (4), which is
bounded. The coordinates of corner points L, C and M are (0,5),
(4,3) and (0,6) respectively. The graph is as follows:-

16. •Now we evaluate Z = 200x + 500y at
these points.
•Hence, minimum value of Z is 2300
attained at the point (4, 3)

17. Thank you
PROJECT BY – mohd. Shibran sajid
XII – B
33