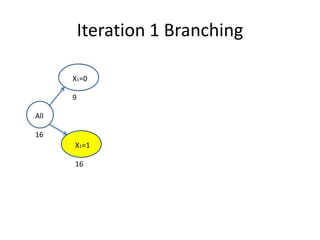
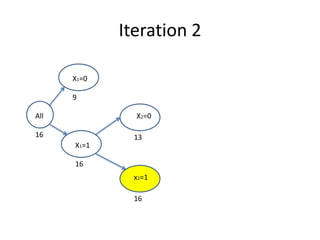
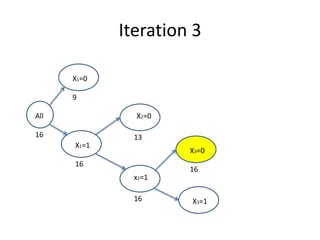
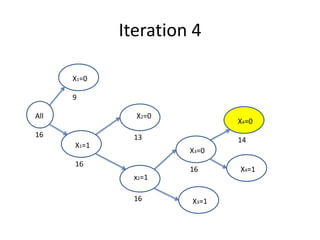
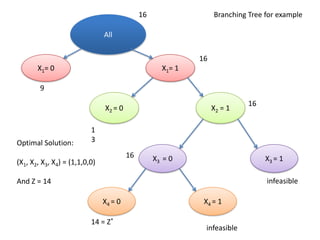
1. The branch and bound algorithm divides the problem into sub-problems by fixing variables to 0 or 1. 2. It bounds sub-problems by relaxing constraints and solving the linear programming relaxation to obtain bounds. 3. Sub-problems are discarded if their bound is less than the best known solution or they are infeasible. 4. The algorithm proceeds by branching on the next variable until no sub-problems remain, leaving the optimal solution.

1. Branch and Bound Algorithm:
Its Application to Binary Integer
Programming
A.Tannouri

2. Concept
The idea behind the branch and bound
algorithm is to “Divide and Conquer”. This is
achieved by:
• Branching
• Bounding
• Fathoming

3. Branching
• Break the original problem into more manageable
smaller parts called sub-problems
• Do this by fixing one of the variables (say x1) so
that x1=0 for the first sub-problem and x1=1 in the
second sub-problem
X1 = 0
Whole
Problem
with ALL
feasible
solutions X1 = 1

4. Bounding
• The goal is to find a bound on how good the best
feasible solution can be for each sub-problem.
• This is done by relaxing a constraint (typically the
binary constraint). This type of relaxation is called
LP relaxation.
• Using the simplex method solve the problem and
get the value of Z
• Any Z value that is found as a can be rounded
down to make it an integer if it isn’t one already

5. Fathoming
• The goal is to determine what sub-problems
we can dismiss from consideration. If it is
“fathomed” then it is dismissed
• A sub-problem is fathomed if it passes one of
the following tests:
• Test 1: Its bound ≤ Z*
• Test 2: Its LP relaxation has no feasible solutions
• Test 3: If an integer is obtained as the optimal solution
for the LP relaxation

6. Summary
1. Find the bound for the original problem by using LP relaxation and
set Z=Z*
2. Branch the problem creating 2 sub-problems and set x1=0 for the
first sub-problem and x1=1 for the second problem
3. Bound the problem by using the simplex method to its LP relaxation
to get an optimal solution, if it’s not an integer then round down.
The integer value of Z is the bound for the sub-problem
4. Apply the fathoming tests to discard sub-problems
5. Repeat step 2 by fixing the next variable (x2,x3,…,xn) and setting it
equal to 0 and 1 for the next two sub-problems and continue with
step 3 and 4.
6. Continue this process until there are no remaining sub-problems.
Once this occurs the current incumbent (Z*) is optimal

7. Initial Problem
• Maximize: Z=9x1+5x2+6x3+4x4
• Sub. to
– (1) 6x1+3x2+5x3+2x4 ≤10
– (2) x3+ x4 ≤1
– (3) –x1 + x3 ≤0
– (4) -x2 + x4≤0
– (5) xj is binary, j=1, 2, 3, 4

8. Sub-problem 1
• Let x1=0
• Maximize: Z=5x2+6x3+4x4
• Sub. to
– (1) 3x2+5x3+2x4 ≤10
– (2) x3+ x4 ≤1
– (3) + x3 ≤0
– (4) -x2 + x4≤0
– (5) xj is binary, j=2, 3, 4

9. Sub-problem 2
• Let x1=1
• Maximize: Z=9+5x2+6x3+4x4
• Sub. to
– (1) 3x2+5x3+2x4 ≤4
– (2) x3+ x4 ≤1
– (3) + x3 ≤1
– (4) -x2 + x4 ≤0
– (5) xj is binary, j=2, 3, 4

10. Relaxation
• To obtain a bound on how good the best
feasible solution is, (5) is “relaxed”
– New (5) 0 ≤ xj ≤ 1, for j=1, 2, 3, 4
• By the simplex method…
– (x1, x2, x3, x4)=(5/6, 1, 0, 1)
– Z=16.5
• Bound for the problem: Z≤16

11. Relaxation of Sub-problems
• Sub-problem 1: (5) x1 ≤ 1 and 0 ≤ xj ≤ 1
– By the simplex method…
• (x1, x2, x3, x4)=(0, 1, 0, 1)
• Z=9
• Sub-problem 2: (5) 0 ≤ x1 and 0 ≤ xj ≤ 1
– By the simplex method…
• (x1, x2, x3, x4)=(1, 4/5, 0, 4/5)
• Z=16.5 Z = 16 (since Z must be integer)
• Go with sub-problem 2; x1=1

12. Iteration 1 Branching
X1=0
9
All
16
X1=1
16

13. Iteration 2;
Sub-problem 3
• Let x1=1, x2=0
• Maximize: Z=9+6x3+4x4
• Sub to
– (1) 5x3+2x4 ≤4
– (2) x3+ x4 ≤1
– (3) x3 ≤1
– (4) x4 ≤0
– (5) xj is binary, j=3, 4

14. Iteration 2;
Sub-problem 4
• Let x1=1, x2=1
• Maximize: Z=14+6x3+4x4
• Sub to
– (1) 5x3+2x4 ≤1
– (2) x3+ x4 ≤1
– (3) x3 ≤1
– (4) x4 ≤1
– (5) xj is binary, j=3, 4

15. Relaxation of Sub-problems
• Sub-problem 3: (5) x1 ≤ 1, x2 ≤ 0, and 0 ≤ xj ≤ 1
– By the simplex method…
• (x1, x2, x3, x4)=(1, 0, 4/5, 0)
• Z=13 4/5
• Sub-problem 4: (5) x1 ≤ 1, x2 ≤ 1, and 0 ≤ xj ≤ 1
– By the simplex method…
• (x1, x2, x3, x4)=(1, 1, 0, 1/2)
• Z=16
• Go with sub-problem 4; x1=1, x2=1

16. Iteration 2
X1=0
9
All X2=0
16 13
X1=1
16
x2=1
16

17. Iteration 3;
Sub-problem 5
• Let x1=1, x2=1 , x3=0
• Maximize: Z=14+4x4
• Sub to
– (1) 2x4 ≤1
– (2) x4 ≤1
– (4) x4 ≤1
– (5) x4 is binary

18. Iteration 3;
Sub-problem 6
• Let x1=1, x2=1 , x3=1
• Maximize: Z=20+4x4
• Sub to
– (1) 2x4 ≤-4
– (2) x4 ≤0
– (4) x4 ≤1
– (5) x4 is binary

19. Relaxation of Sub-problems
• Sub-problem 5: (5) x1 ≤ 1, x2 ≤ 1, x3 ≤ 0, and 0 ≤
xj ≤ 1
– By the simplex method…
• (x1, x2, x3, x4)=(1, 1, 0, 1/2)
• Z=16
• Sub-problem 6: (5) x1 ≤ 1, x2 ≤ 1, x3 ≤ 1, and 0 ≤
xj ≤ 1
– There are no feasible solutions
• Go with sub-problem 5; x1=1, x2=1 , x3=0

20. Iteration 3
X1=0
9
All X2=0
16 13
X1=1
X3=0
16
16
x2=1
16 X3=1

21. Iteration 4
• x4=0
– (x1, x2, x3, x4)=(1, 1, 0, 0) is feasible
– Z=14
• x4=1
– (x1, x2, x3, x4)=(1, 1, 0, 1) is infeasible

22. Iteration 4
X1=0
9
All X2=0
X4=0
16 13 14
X1=1
X3=0
16
16 X4=1
x2=1
16 X3=1

23. 16 Branching Tree for example
All
16
X1 = 0 X1 = 1
9
16
X2 = 0 X2 = 1
1
Optimal Solution: 3
16 X3 = 0 X3 = 1
(X1, X2, X3, X4) = (1,1,0,0)
And Z = 14 infeasible
X4 = 0 X4 = 1
14 = Z*
infeasible