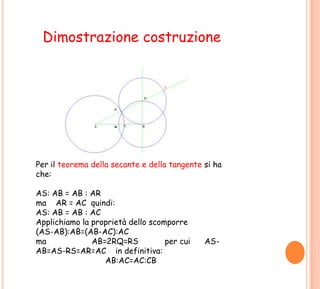
Il documento discute il lavoro multidisciplinare sul tema 'i numeri e la geometria nell'arte', presentato dalla classe 2G sotto la guida del prof. Amato-Valentino. Viene approfondito il concetto di sezione aurea, descrivendo la sua costruzione e applicazione nel contesto del rettangolo aureo e della spirale aurea. Si evidenzia l'importanza di questi elementi nel design e nell'arte, sottolineando il loro valore estetico e matematico.

1. LAVORO
MULTIDISCIPLINARE:
“I NUMERI E LA
GEOMETRIA NELL’ARTE
CLASSE 2G
PROF. AMATO - VALENTINO
A.S. 2012-2013

2. VISITA GUIDATA CITTA' DELLA SCIENZA 22/02/2013 CLASSE 2G
Laboratorio:I Numeri e la Geometria nell'Arte
RACCOLTA FOTO LAVORI
RETTANGOLO AUREO
TASSELLAZIONE

3. LAVORI EFFETTUATI COL PROFESSORE DI ARTE

4. SEZIONE AUREA DI UN SEGMENTO
DEF
Dicesi parte aurea o sezione aurea di un
segmento quella parte del segmento che è
media proporzionale tra l'intero segmento
e la parte rimanente

5. COSTRUZIONE DELLA PARTE AUREA
DI UN SEGMENTO
Per costruire la sezione aurea di un segmento AB
assegnato si procede nel modo seguente:
- si costruisce la circonferenza di centro B e raggio
uguale alla metà del segmento AB,
- si traccia la perpendicolare al segmento a AB
passante per B,
- segnato il punto Q intersezione di tale retta con la
circonferenza, si traccia la circonferenza di centro Q
e passante per B,
- si disegna quindi la retta passante per A e per Q,
- segnato il punto R intersezione di tale retta con la
circonferenza,
- si costruisce la circonferenza di centro A e passante
per R,
- si segna il punto C intersezione di quest'ultima
circonferenza con il segmento AB.

6. Dimostrazione costruzione
Per il teorema della secante e della tangente si ha
che:
AS: AB = AB : AR
ma AR = AC quindi:
AS: AB = AB : AC
Applichiamo la proprietà dello scomporre
(AS-AB):AB=(AB-AC):AC
ma AB=2RQ=RS per cui AS-
AB=AS-RS=AR=AC in definitiva:
AB:AC=AC:CB

7. RAPPORTO AUREO
Il rapporto AB/AC si chiama rapporto aureo e
si indica di solito con la lettera φ ed ha un
valore numerico preciso che si può ricavare in
questo modo
AB:AC=AC:BC
φ = AB/AC = (1+√5)/2 ≈1,618
Questo significa che se poniamo uguale a 1
la lunghezza del segmento AB la sua parte
aurea vale 0,618

8. RETTANGOLO AUREO
Esiste uno speciale rettangolo, le cui dimensioni
corrispondono al segmento dato e alla sua sezione
aurea, detto rettangolo aureo.
Un rettangolo Aureo è il più armonioso, il più bello
tra gli infiniti rettangoli disegnabili.

9. SPIRALE AUREA
Se all'interno di un rettangolo aureo, si disegna un
quadrato che ha il lato uguale al lato minore
del rettangolo, cioè di lato la sezione aurea, si
ottiene per differenza un rettangolo che è a sua
volta un rettangolo aureo.
Ripetendo l'operazione per un minimo di cinque
volte nei vari rettangoli per differenza che
risultano, si otterrà la spirale aurea detta anche
spirale logaritmica, ottenuta tracciando una serie
di archi circolari che abbiano come raggio i lati dei
quadrati.