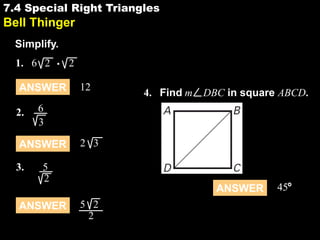
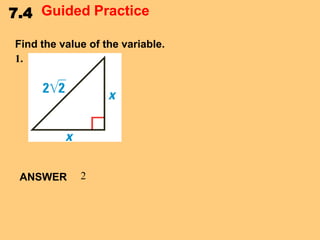
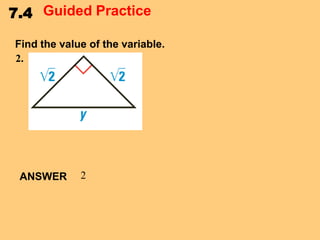
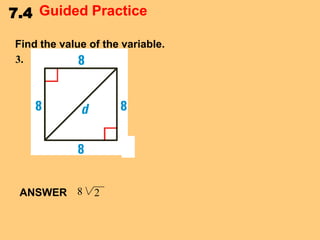
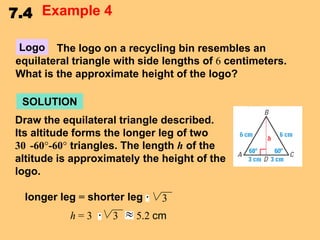
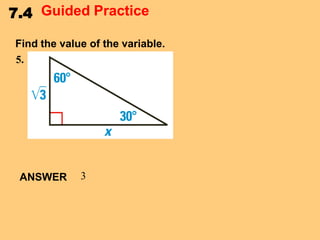
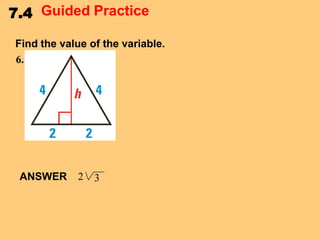
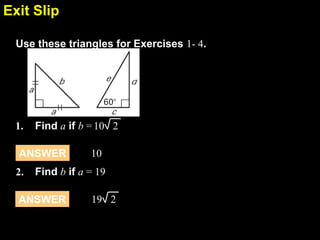
This document discusses special right triangles and their properties. It begins by defining special right triangles as those with angles of 45-45-90 degrees or 30-60-90 degrees. Examples are then provided of using the properties of these triangles to find missing side lengths or angle measures. The document concludes with guided practice problems for students to practice applying special right triangle properties.

1. 7.4 Special Right Triangles
7.4
Bell Thinger
Simplify.
1. 6 2
ANSWER
2.
12
4. Find m
DBC in square ABCD.
6
3
ANSWER
3.
2
2 3
5
2
ANSWER
ANSWER
5 2
2
45

2. 7.4

3. Example 1
7.4
Find the length of the hypotenuse.
a.
SOLUTION
a. By the Triangle Sum Theorem, the measure of the
third angle must be 45º. Then the triangle is a
45º- 45º- 90º triangle, so by Theorem 7.8, the
hypotenuse is 2 times as long as each leg.
hypotenuse = leg .
=8 2
2
45 - 45°- 90° Triangle Theorem
Substitute.

4. Example 1
7.4
Find the length of the hypotenuse.
b.
SOLUTION
b. By the Base Angles Theorem and the Corollary
to the Triangle Sum Theorem, the triangle is a
45º- 45º- 90º triangle.
hypotenuse = leg .
=3
2 .
=3.2
=6
2
45 - 45°- 90° Triangle Theorem
2
Substitute.
Product of square roots
Simplify.

5. 7.4 Example 2
Find the lengths of the legs in the
triangle.
SOLUTION
By the Base Angles Theorem and the Corollary to the
Triangle Sum Theorem, the triangle is a 45º- 45º- 90º
triangle.
hypotenuse = leg
2
5
2 =x
2
5
x 2
2
=
2
2
5=x
45 - 45°- 90° Triangle Theorem
Substitute.
Divide each side by
Simplify.
2

6. 7.4 Example 3
SOLUTION
By the Corollary to the Triangle Sum Theorem, the
triangle is a 45º- 45º- 90º triangle.
hypotenuse = leg
WX = 25
2
2
45 - 45°- 90° Triangle Theorem
Substitute.
ANSWER The correct answer is B.

7. 7.4 Guided Practice
Find the value of the variable.
1.
ANSWER
2

8. 7.4 Guided Practice
Find the value of the variable.
2.
ANSWER
2

9. 7.4 Guided Practice
Find the value of the variable.
3.
ANSWER 8
2

10. 7.4 Guided Practice
4. Find the leg length of a 45°- 45°- 90° triangle with a
hypotenuse length of 6.
ANSWER 3
2

11. 7.4

12. 7.4 Example 4
Logo The logo on a recycling bin resembles an
equilateral triangle with side lengths of 6 centimeters.
What is the approximate height of the logo?
SOLUTION
Draw the equilateral triangle described.
Its altitude forms the longer leg of two
30 -60°-60° triangles. The length h of the
altitude is approximately the height of the
logo.
longer leg = shorter leg
h=3
3
3
5.2 cm

13. 7.4 Example 5
Find the values of x and y. Write your
answer in simplest radical form.
STEP 1 Find the value of x.
longer leg = shorter leg
9=x 3
9
=x
3
9
3 =x
3
3
9 3
=x
3
3 3 =x
3
30° - 60° - 90° Triangle Theorem
Substitute.
Divide each side by
3
Multiply numerator and
denominator by 3
Multiply fractions.
Simplify.

14. 7.4 Example 5
STEP 2
Find the value of y.
hypotenuse = 2 shorter leg
y=2
3 3 =6 3
30° - 60° - 90° Triangle Theorem
Substitute and simplify.

15. 7.4 Example 6
Dump Truck The body of a
dump truck is raised to empty
a load of sand. How high is
the 14 foot body from the
frame when it is tipped
upward at the given angle?
a. 45 angle
b. 60° angle
SOLUTION
a. When the body is raised 45 above
the frame, the height h is the
length of a leg of a 45°- 45°- 90°
triangle. The length of the
hypotenuse is 14 feet.

16. 7.4 Example 6
14 = h 2
14
=h
2
9.9
h
45° - 45° - 90° Triangle Theorem
Divide each side by
2
Use a calculator to approximate.
When the angle of elevation is 45 , the body is about
9 feet 11 inches above the frame.

17. 7.4 Example 6
b. When the body is raised 60°, the
height h is the length of the longer
leg of a 45°- 45°- 90° triangle. The
length of the hypotenuse is 14 feet.
hypotenuse = 2 shorter leg
14 = 2 s
7 =s
longer leg = shorter leg
h =7 3
h
12.1
30° - 60° - 90° Triangle Theorem
Substitute.
Divide each side by 2.
3
30° - 60° - 90° Triangle Theorem
Substitute.
Use a calculator to approximate.
When the angle of elevation is 60 , the body is about
12 feet 1 inch above the frame.

18. 7.4 Guided Practice
Find the value of the variable.
5.
ANSWER
3

19. 7.4 Guided Practice
Find the value of the variable.
6.
ANSWER
2
3

20. 7.4 Guided Practice
8. In a 30°- 60°- 90° triangle, describe the location of
the shorter side. Describe the location of the
longer side?
SAMPLE ANSWER
The shorter side is adjacent to the 60° angle, the
longer side is adjacent to the 30° angle.

21. Exit Slip
7.4
Use these triangles for Exercises 1- 4.
1.
Find a if b = 10 2
ANSWER
2.
10
Find b if a = 19
ANSWER
19 2

22. Exit Slip
7.4
Use these triangles for Exercises 1- 4.
3.
Find d and e if c = 4.
d=4 3,e=8
ANSWER
4. Find c and d if e = 50 3 .
ANSWER
c = 25 3 , d = 75

23. Exit Slip
7.4
5.
Find x, y and z.
ANSWER
x= 3 2 ,y= 3 6 ,z= 6 2

24. 7.4
Homework
Pg
#