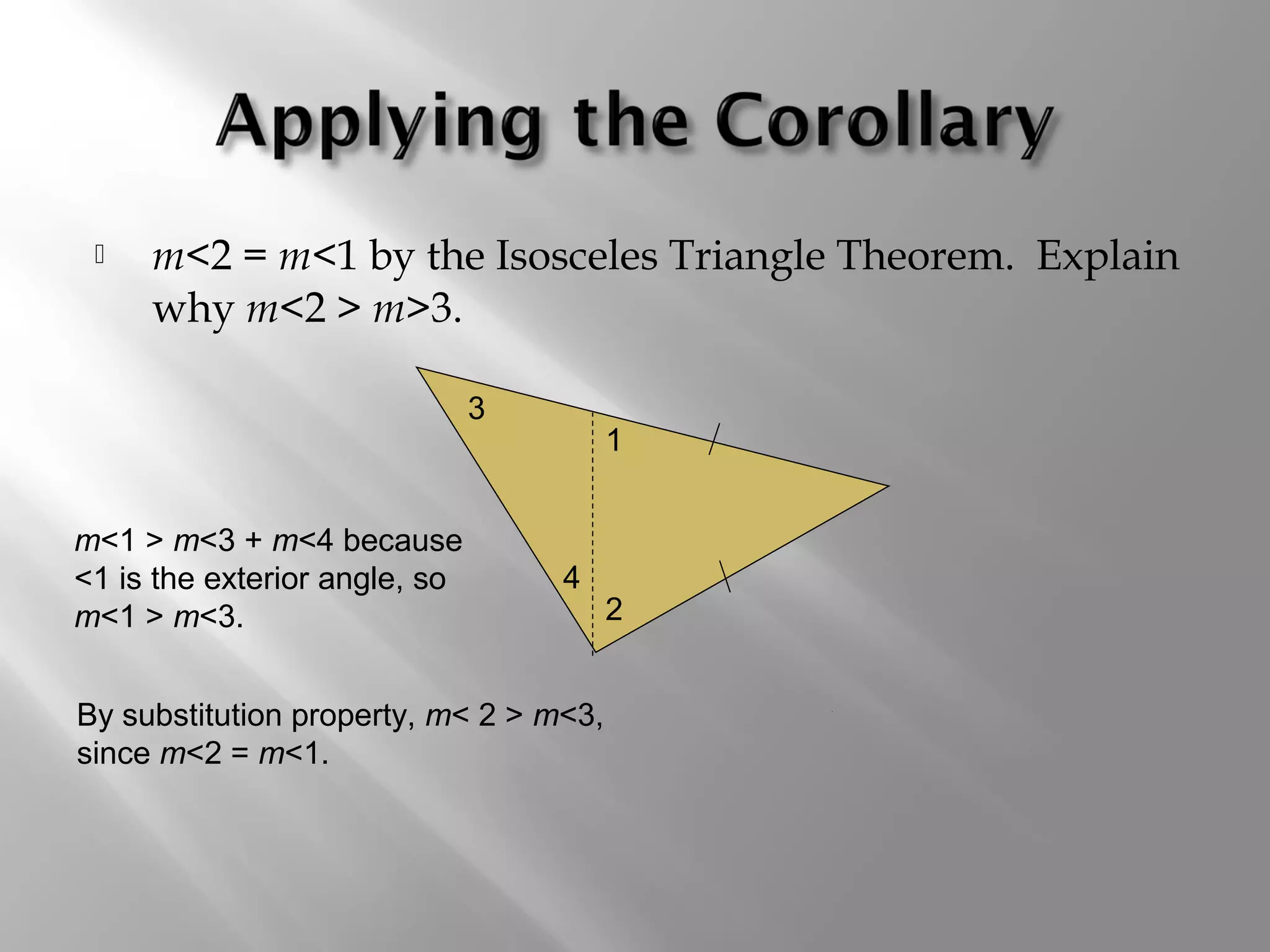
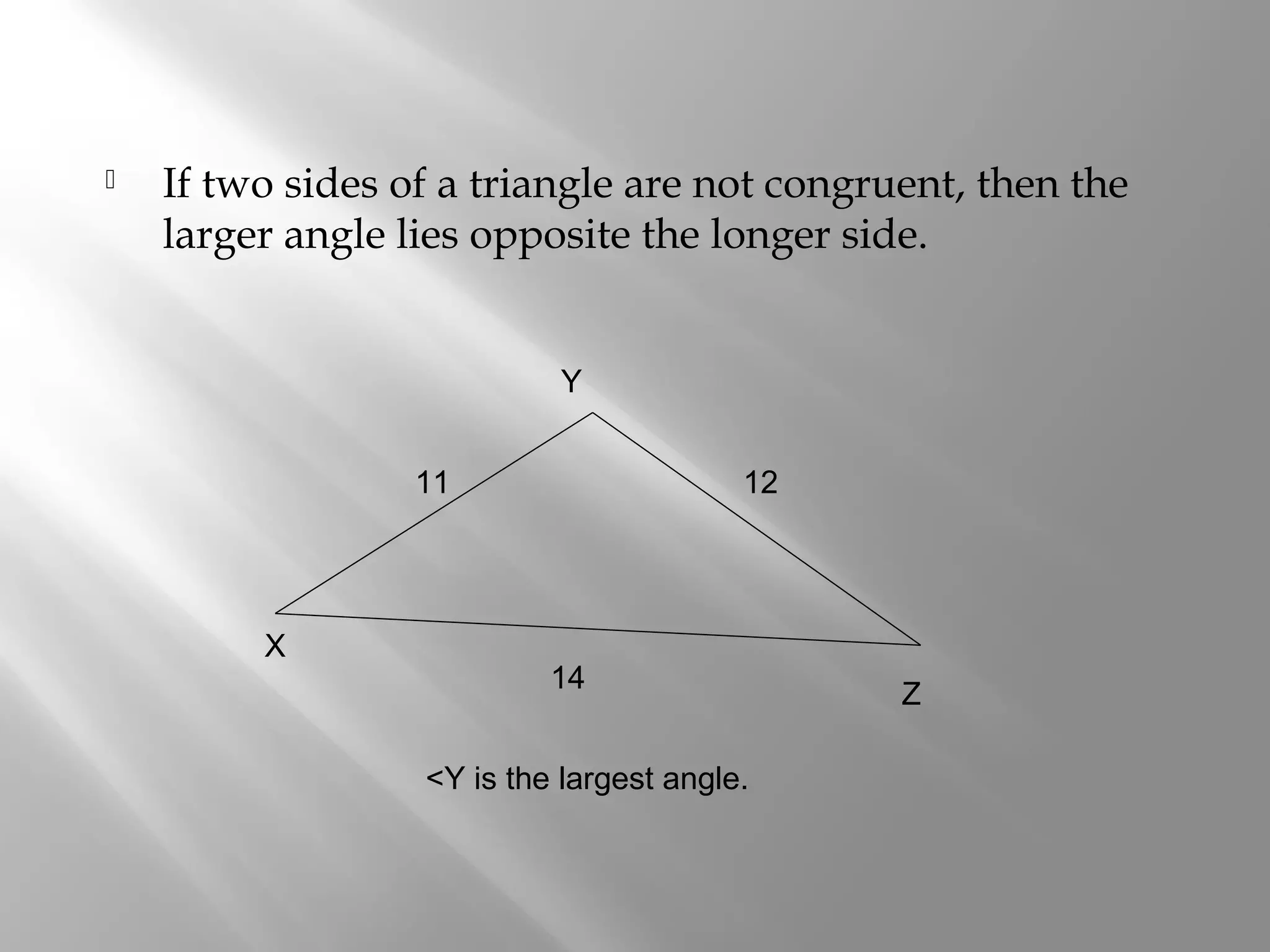
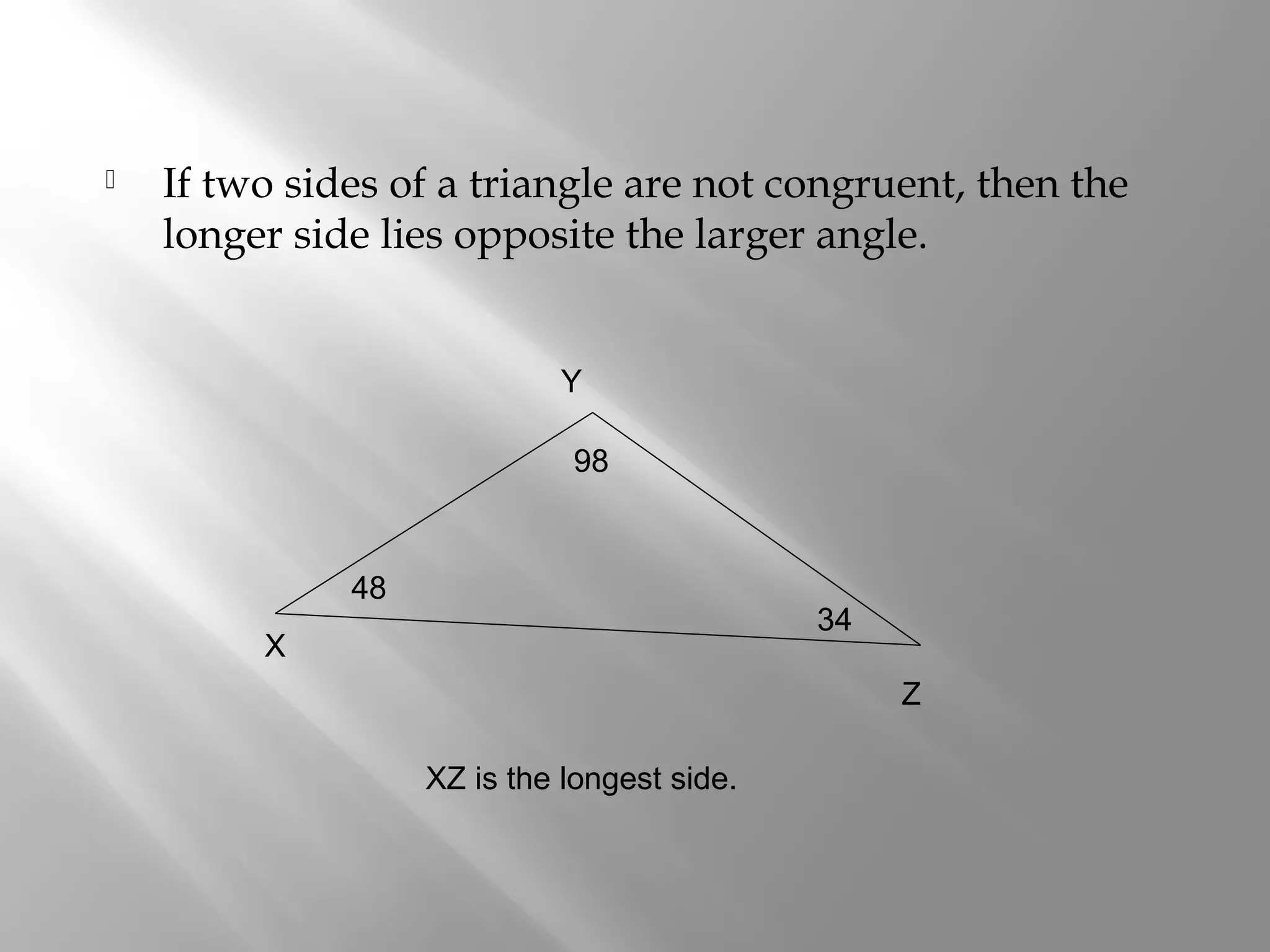
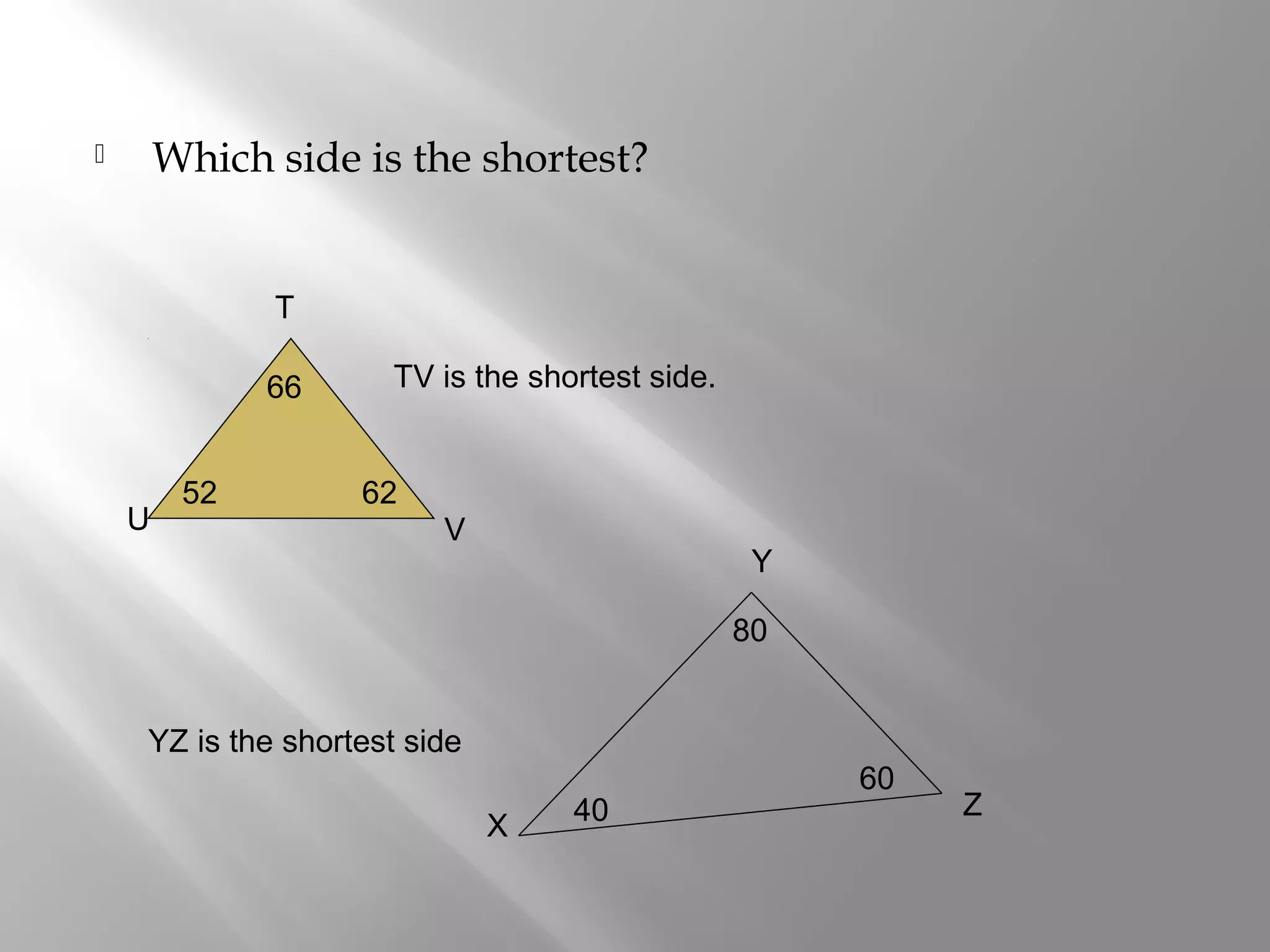
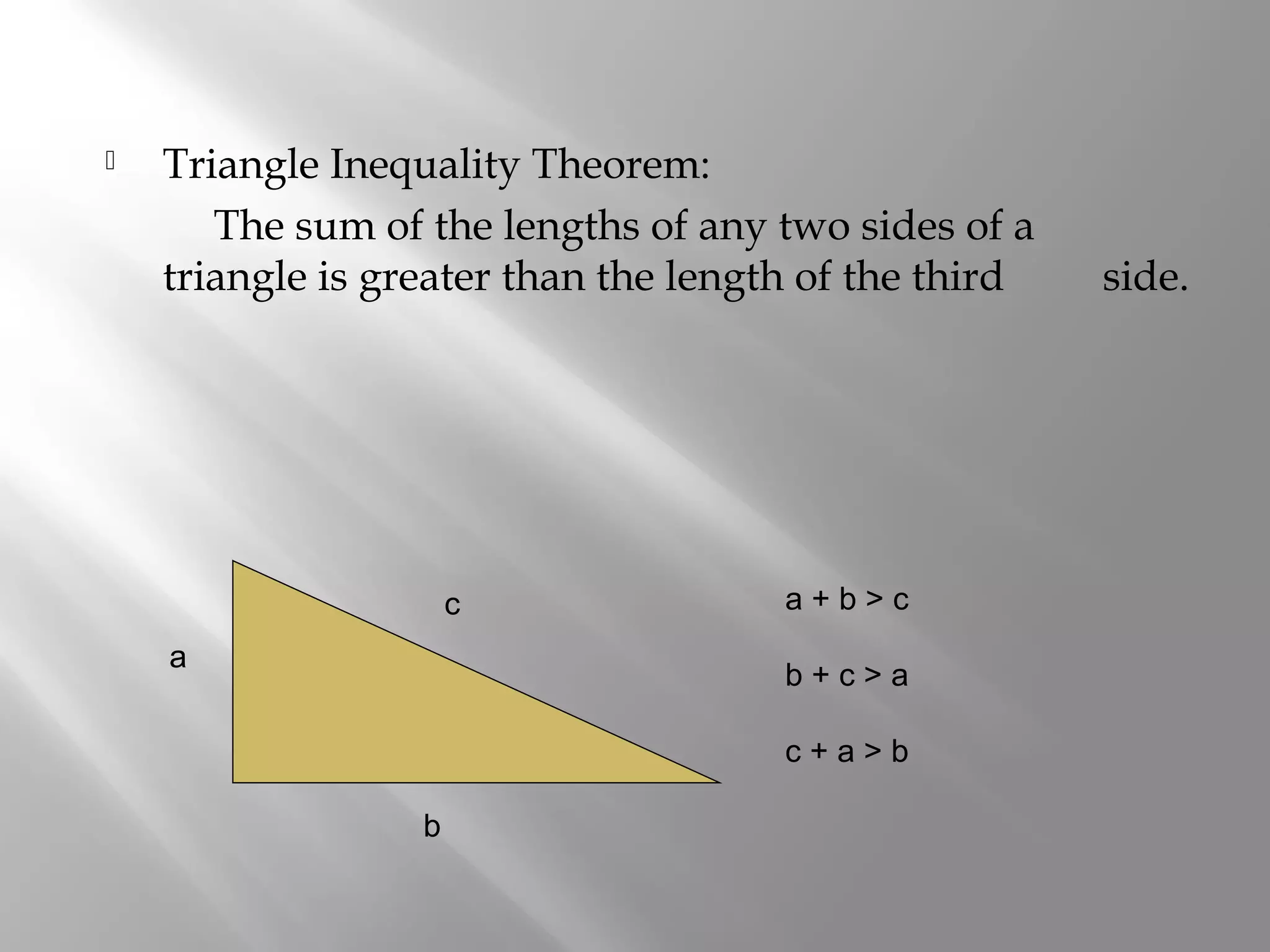
This document contains explanations and examples regarding triangle theorems and properties including: the exterior angle theorem, isosceles triangle theorem, relationship between side length and angle size, triangle inequality theorem, and determining possible third side lengths given two sides of a triangle. Examples are provided to demonstrate applying these triangle concepts to determine largest angles, longest/shortest sides, and possible side lengths.

2.  Corollary to the Triangle Exterior Angle Theorem:
The measure of an exterior angle of a triangle is
greater than the measure of each of its remote
interior angles.
2
3
1
m<1 > m<2 and m<1 > m<3

3.  m<2 = m<1 by the Isosceles Triangle Theorem. Explain
why m<2 > m>3.
1
2
4
3
m<1 > m<3 + m<4 because
<1 is the exterior angle, so
m<1 > m<3.
By substitution property, m< 2 > m<3,
since m<2 = m<1.

4.  If two sides of a triangle are not congruent, then the
larger angle lies opposite the longer side.
X
Y
11 12
14 Z
<Y is the largest angle.

5.  A landscape architect is designing a triangular deck.
She wants to place benches in the two larger corners.
Which corners have the larger angles?
27ft
21ft
A
18ft
B
C
<B and <A are the larger angles, <C is the smallest.

6.  If two sides of a triangle are not congruent, then the
longer side lies opposite the larger angle.
X
Y
Z
48
98
34
XZ is the longest side.

7.  Which side is the shortest?
66
TV is the shortest side.
52 62
U
T
V
40
60
X
Y
Z
80
YZ is the shortest side

8.  Triangle Inequality Theorem:
The sum of the lengths of any two sides of a
triangle is greater than the length of the third side.
a
b
c a + b > c
b + c > a
c + a > b

9.  Can a triangle have sides with the given lengths?
 3ft, 7ft, 8ft
Yes, 3 + 7 = 10 and 10 > 8
 3cm, 6cm, 10cm
No, 3 + 6 = 9 and 9 is not greater than 10

10.  Can a triangle have sides with the given lengths?
 2m, 7m, 9m
No, 2 + 7 = 9, and 9 is not greater than 9
 4yd, 6yd, 9yd
Yes, 4 + 6 = 10 and 10 is greater than 9

11.  A triangle has side lengths of 8cm and 10cm. Describe
the possible lengths of the third side.
To answer this kind of question, add the numbers together and
Subtract the small number from the larger number.
8 + 10 = 18 10 – 8 = 2
The value of the third side must be greater
Than 2 and less than 18.
(x > 2 and x < 18)
2cm < x < 18cm

12.  A triangle has side lengths of 3in and 12in. Describe
the possible lengths of the third side.
To answer this kind of question, add the numbers together and
Subtract the small number from the larger number.
3 + 12 = 15 12 – 3 = 9
The value of the third side must be greater
Than 9 and less than 15. (x > 9 and x < 15)
9in < x < 15in

13. All rights belong to their respective owners.
Copyright Disclaimer Under Section 107 of
the Copyright Act 1976, allowance is made
for "fair use" for purposes such as criticism,
comment, news reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted by copyright
statute that might otherwise be infringing.
Non-profit, EDUCATIONAL or personal use
tips the balance in favor of fair use.