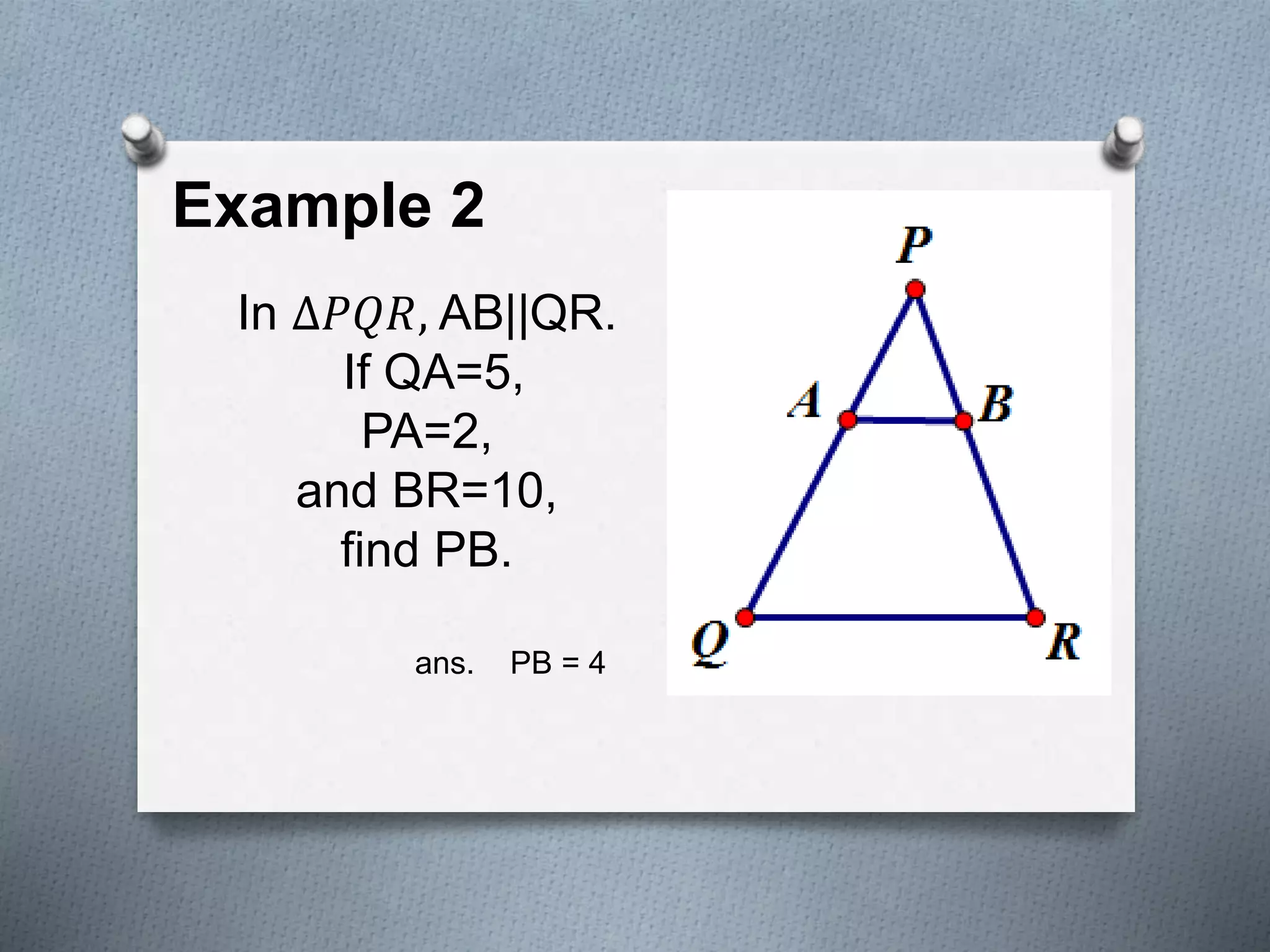
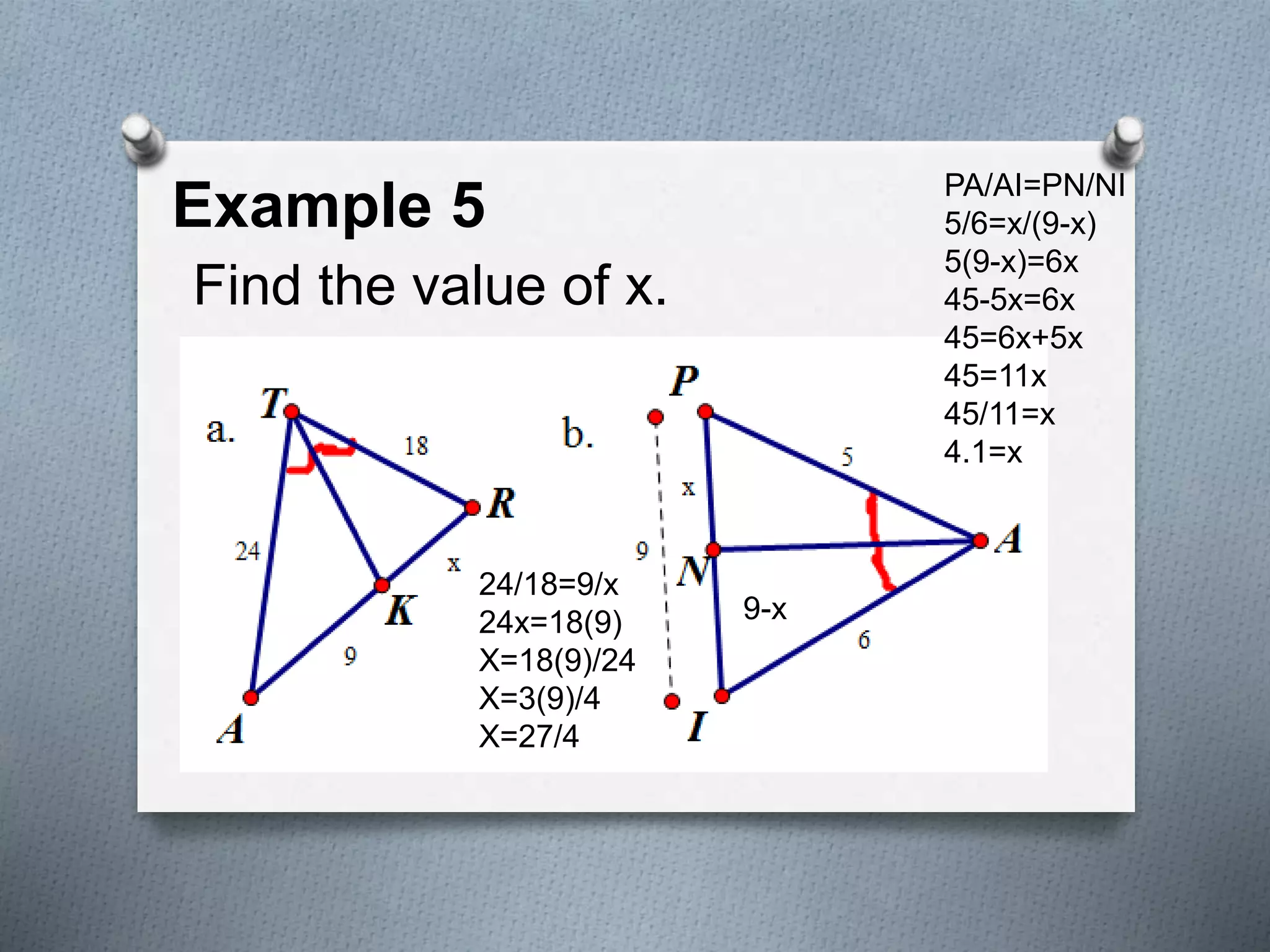
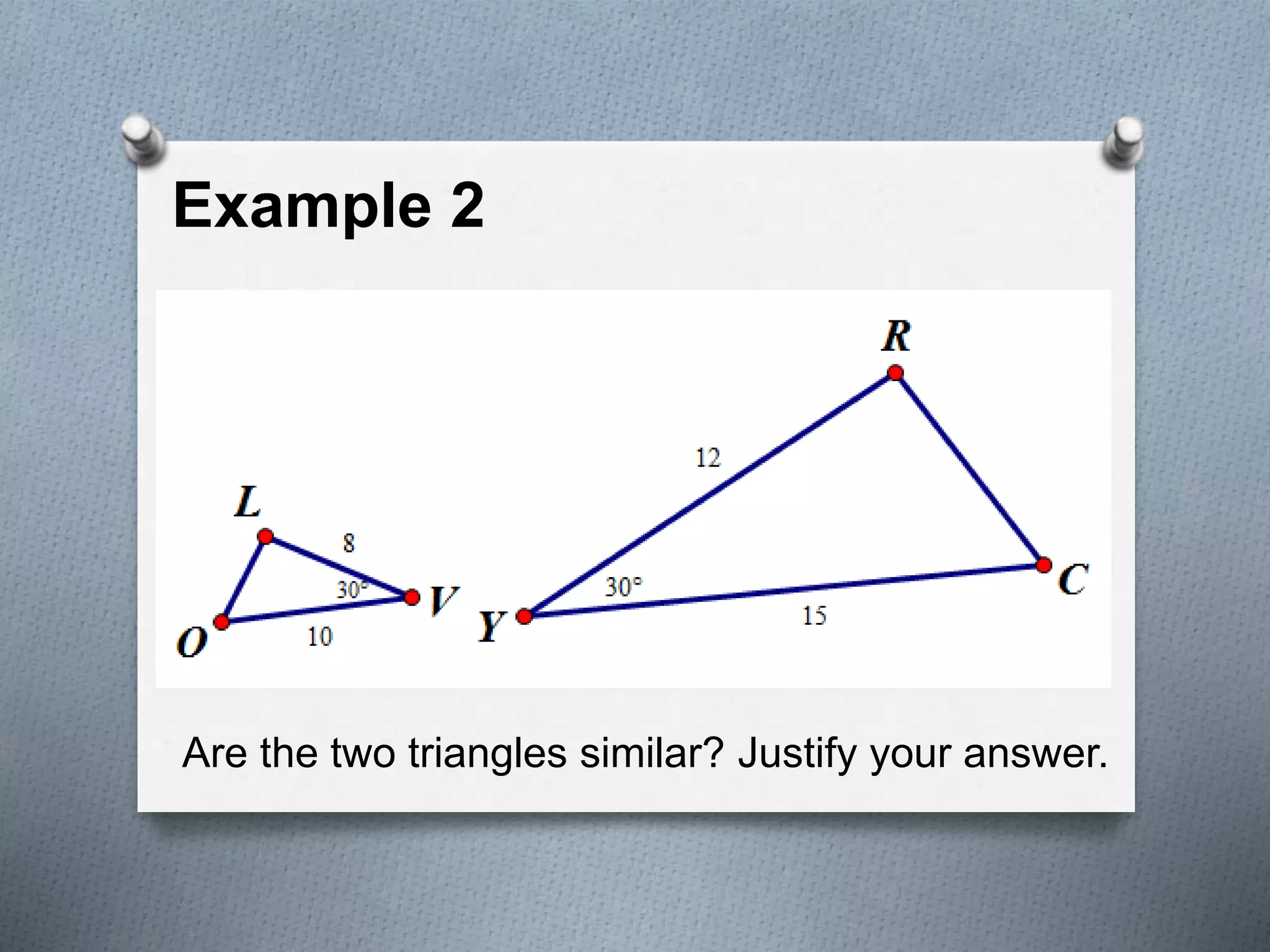
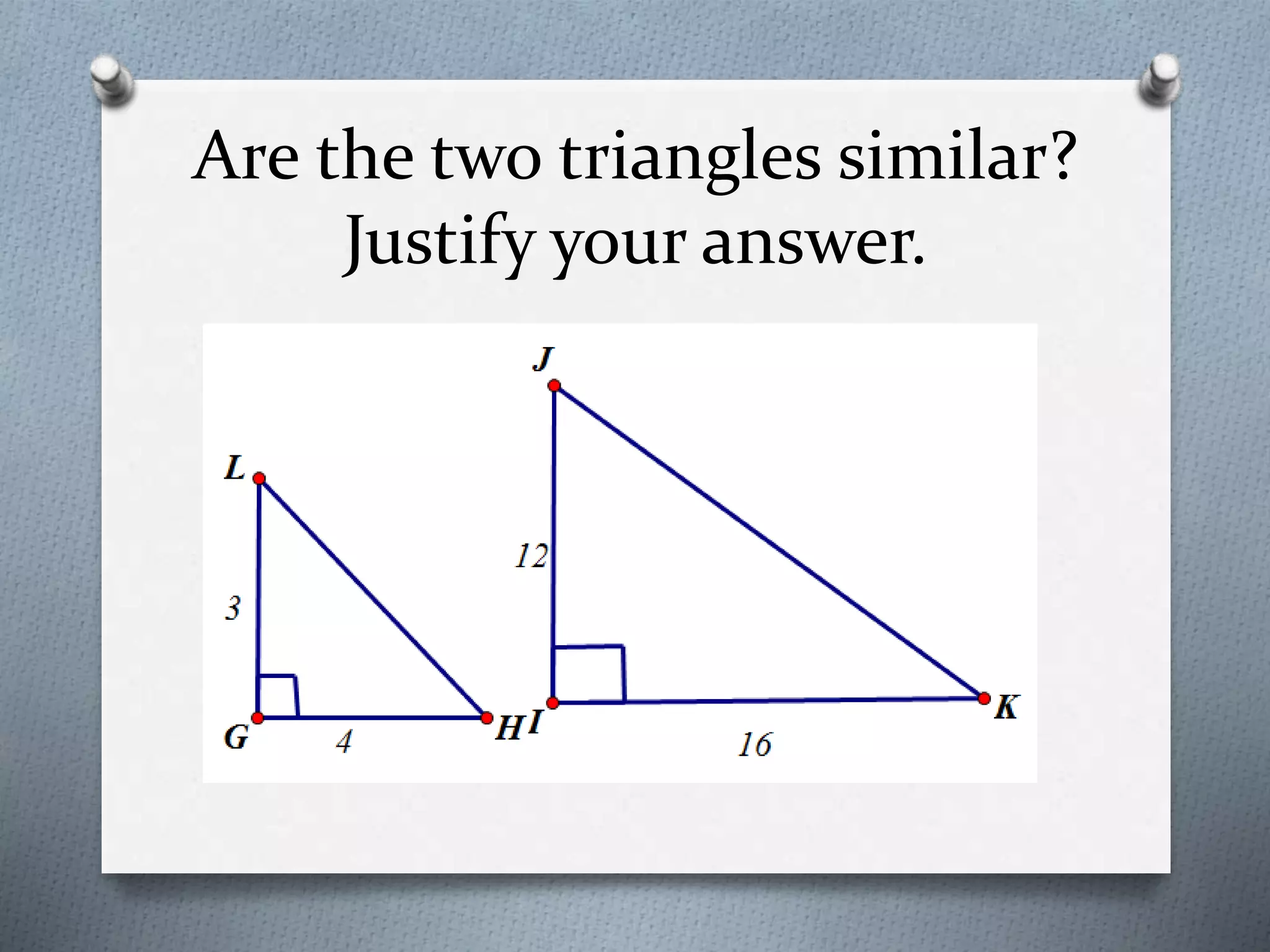
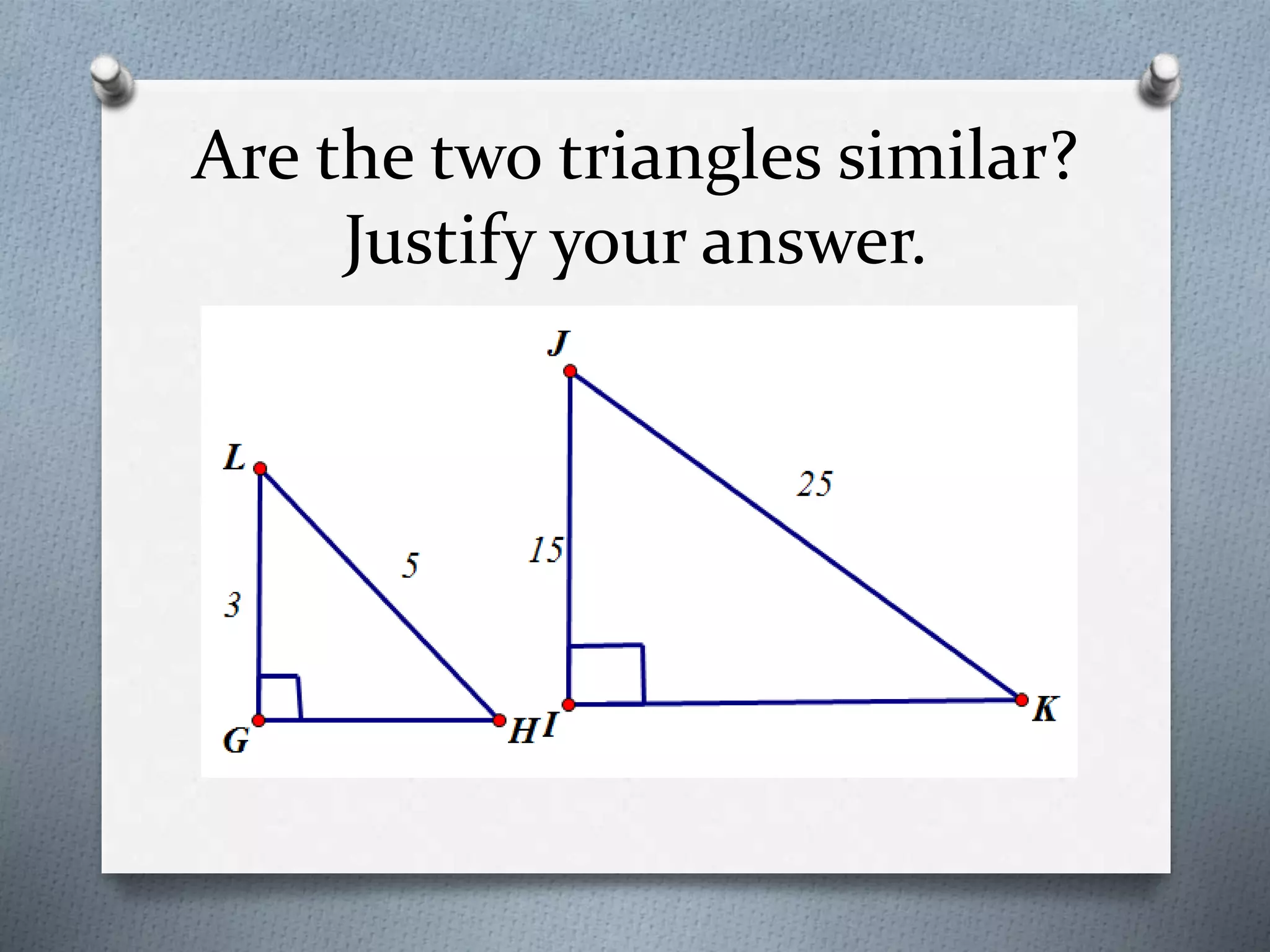
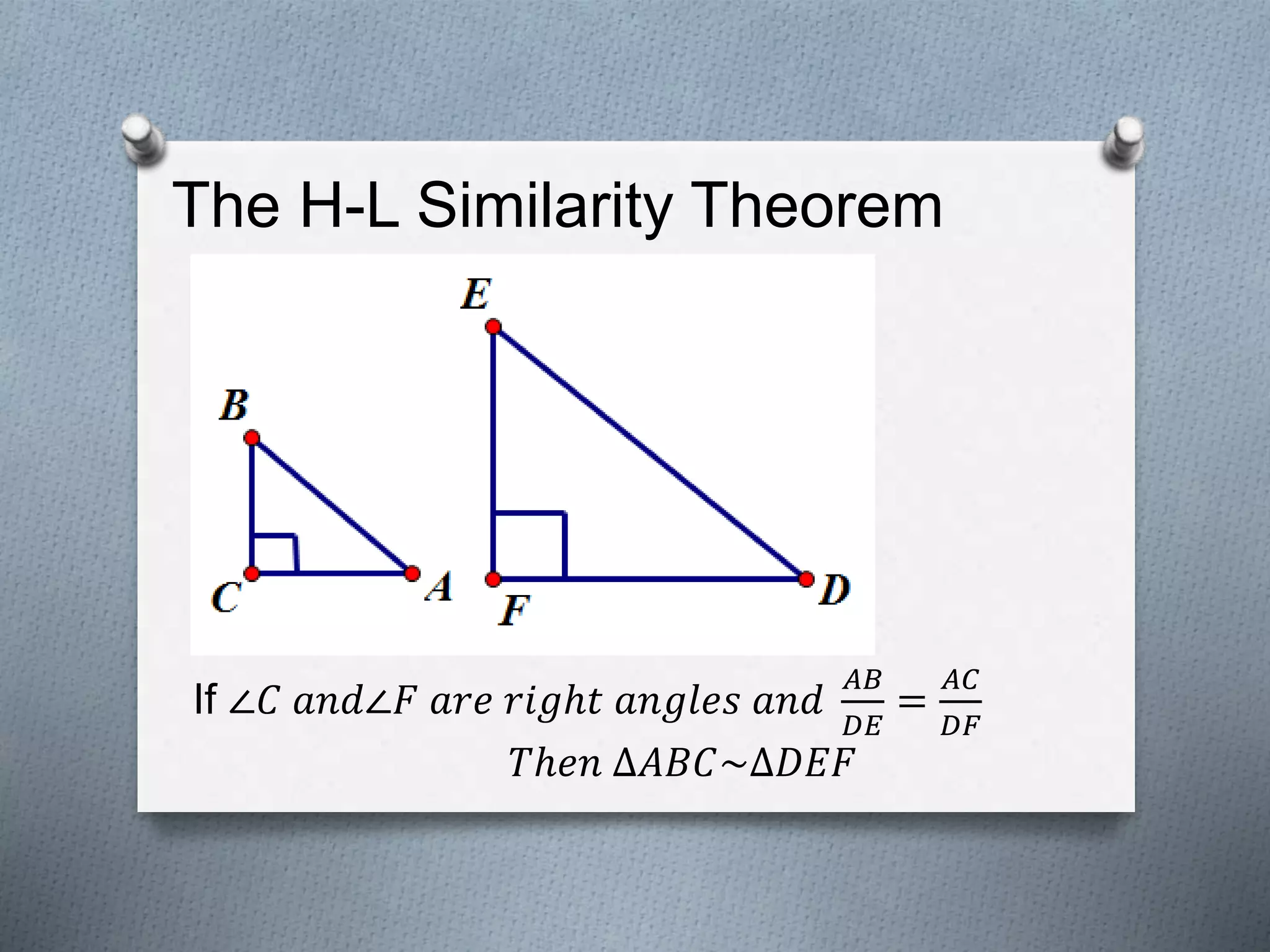
The document discusses the concept of similarity in geometry, focusing on topics such as the properties and criteria for similar polygons and triangles, including the basic proportionality theorem and angle bisector theorem. It explains the significance of ratios and proportional relationships, providing examples of calculations and properties of similar figures. Additionally, it covers theorems related to similarity, including AAA, SAS, and SSS, and discusses how the ratios of perimeters and areas are related to similarity.

1. SIMILARITY
O 5.1 Introduction
5.2 Ratio And Proportionality
5.3 Similar Polygons
5.4 Basic Proportionality Theorem
5.5 Angle Bisector Theorem
5.6 Similar Triangles
5.7 Properties Of Similar Triangles

2. SIMILARITY
O 5.1 Introduction
O The concept of similarity bears close
resemblance to the concept of
congruence. Congruent figures are exact
replicas of each other. They have the
same shape and the same size. Now
consider figures that have the same
shape but not the same size. Such figures
look 'similar' but in essence are simply
proportionate to each other.

3. SIMILARITY
O 5.2 Ratio and Proportionality
O Ratio is a comparison of two numbers
expressed in the simplest fraction form. If
a city covers an area of 100 square miles
and another city covers 200 square miles,
the 'ratio' of their area is expressed as 100
: 200 or on simplification 1 : 2. This means
that the second city is twice as large as
the first.

4. Ratio and
Proportionality
O If in a linear pair the ratio of angles is 1 :
2, it is possible to find the exact measure
of both the angles.

5. O Example 5.2.1
If the measure of the smaller angle is x, the
measure of the bigger angle is 2x. Therefore x :
2x = 1 : 2.
O Since a linear pair of angles sum up to 1800
x + 2x = 1800
3x = 1800
x = 600
therefore 2x = 1200
The two angles are 600 and 1200
Ratio and
Proportionality

6. O Proportionality : Compare the drawing of
a bridge on a paper with the actual
structure. They look similar because the
ratios of height to width to length are the
same in both the cases.
O The equation which shows that two ratios
are equal is called proportion. The design
on paper and the actual structure look the
same because they are proportionate to
each other.
Ratio and
Proportionality

7. O Equality in ratios is expressed as follows :
The number at the end i.e. 3 and 10 are called
extremes and the numbers in the middle are
called means.
means
extremes
Ratio and
Proportionality

8. Proportions have four properties.
O 1) Cross Product Property
O This is also called the cross multiplication
property.
If
Ratio and
Proportionality

9. Proportions have four properties.
O 2) Switching or exchange property.
If
Ratio and
Proportionality

10. Proportions have four properties.
O 3) Upside down or inverting property.
If
Ratio and
Proportionality

11. Proportions have four properties.
O 4) Denominator addition or subtraction
property.
Ratio and
Proportionality

12. O Example 1
A segment measuring 10 cm is divided into two
parts in the ratio 1 : 3. What is the length of
each part ?
O Solution:
Let the length of one part of the segment be x
then that of the other will be 3x .
Given that x + 3x = 10 cm.
or 4x = 10 cm.
x = 2.5 cm.
Ratio and
Proportionality
Therefore one segment measures 2.5 cm. and the other 7.5
cm.

13. O Example 2
If the number of apples in a bag is 12 and
the number of peaches is 3, what is the ratio
of apples to peaches ?
3. Two complementary angles are in the
ratio
1 : 2 what is their measure ?
Ratio and
Proportionality

14. 4. A 500 ft tall building is drawn as 25 cm
tall on a paper. If its width is drawn as 2 cm
what is the actual width of the building ?
Ratio and
Proportionality

15. 5.3 Similar Polygons
O Polygons are said to be similar if :
a) there exists a one to one correspondence
between their sides and angles.
b) the corresponding angles are congruent
and
c) their corresponding sides are proportional
in lengths.
Consider the polygons ABCD and LMNO in
the figure 5.1.

16. 5.3 Similar Polygons
figure 5.1.
Their corresponding angles are equal but their
sides are not proportional. Hence they are not
similar.

17. O Now the sides may be proportional but the
angles may not be congruent. For
instance we have polygons like PQRS
and HIJK (figure 5.2)
O Again they are not similar.
5.3 Similar Polygons

18. O Thus to be
similar polygons
must satisfy
both, the
condition of
congruent angles
and that of
proportionate
sides. Figure 5.3
shows some
similar polygons.
5.3 Similar Polygons

19. 5.4 Basic Proportionality
Theorem
O If a line is drawn
parallel to one side of a
triangle and it intersects
the other two sides at
two distinct points then
it divides the two sides
in the same ratio.

20. 5.4 Basic Proportionality
Theorem
O To prove that Join S to R
and Q to T, Consider DPTS and DQTS
Areas of triangles with same height are in
the ratio of their bases.
Figure 5.4 shows triangle
PQR with line l parallel to
seg.QR. l intersects seg. PQ
and seg. PR at S and T
respectively.

21. 𝑙𝑄𝑃
𝐼𝑓 𝑙 || BC,
then
𝐵𝑃
𝐴𝑃
=
𝐶𝑄
𝐴𝑄

22. 5.4 Basic Proportionality
Theorem
O Similarly But A(DQTS) =
A(DSRT) as they have a common base
seg.ST and their heights are same as they
are between parallel lines.
Thus the line l which is parallel to seg.QR
divides seg.PQ and seg.PR in the same
ratio.

23. 5.5 Angle bisector theorem
O In a triangle the angle
bisector divides the opposite
side in the ratio of the
remaining sides. This means
that for a DABC ( figure 5.5)
the bisector of ∠A divides BC
in the ratio .

24. 5.5 Angle bisector theorem
O To prove that
Through C draw a line parallel to seg.AD
and extend seg.BA to meet it at E.
seg.CE || seg.DA
∠BAD ≅ ∠AEC , corresponding angles
∠DAC ≅ ∠ACE , alternate angles
But ∠BAD = ∠DAC , given
Therefore ∠AEC ≅ ∠ACE

25. 5.5 Angle bisector theorem
O Hence DAEC is an isosceles triangle.
Therefore seg.AC ≅ seg.AE
In D BCE, AD||CE
Thus the bisector divides the opposite side in the
ratio of the remaining two sides.

26. If ∆𝐴𝐵𝐶 with AD an
angle bisector, then
𝐴𝐵
𝐴𝐶
=
𝐵𝐷
𝐶𝐷
5.5 Angle bisector theorem

27. Exercises:
O Example 1:
O In the diagram seg.PQ || seg.BC
O l (seg.AP) = 30 ft.
O l (seg.PB) = 20 ft.
O l (seg.QC) = 16 ft.
O Find l (seg.AC).

28. Exercises:
O Solution:

29. Example 2
In ∆𝑃𝑄𝑅, AB||QR.
If QA=5,
PA=2,
and BR=10,
find PB.
ans. PB = 4

30. Example 3
Z

31. Example 4
A flagpole 8m high casts a shadow
of 12m, while a nearby building
casts a shadow of 60m. How high
is a building?
The building is 32m high

32. Example 5
Find the value of x.
PA/AI=PN/NI
5/6=x/(9-x)
5(9-x)=6x
45-5x=6x
45=6x+5x
45=11x
45/11=x
4.1=x
24/18=9/x
24x=18(9)
X=18(9)/24
X=3(9)/4
X=27/4
9-x

33. Exercises:
O Example 6
O In trapezium ABCD, seg.AB || seg.DC.
PQ || DC
O l (seg.AP) = 8, l (seg.PD) = 10
O l (seg.BQ) = 6, find l seg.QC.

34. Exercises:
O Example 7:
If in a triangle PQR a line parallel to QR cuts
PQ and PR at x and y respectively, such
that l(seg.PX) = 12 ,l(seg.XQ) = 8 and
l(seg.PY) = 9, find (seg.YR).

35. Exercises:
O Example 8
O In DABC, seg.BP is the bisector of ∠B. If
O l(seg.AB) = 3, l(seg.BC) = 5 and
O l(seg.AP) = 1.5, find l(seg.PC).

36. 5.6 Similar Triangles
O Two triangles are similar if their corresponding
angles are congruent and their corresponding
sides are proportional. A group of sufficient
conditions is called as a test for similarity.
These tests are based on two basic principles.
O 1) In 2 triangles if the corresponding angles
are congruent, their corresponding sides are
equal.
O 2) If the sides of 2 triangles are proportional
then the corresponding angles are congruent.

37. Similar Triangles

38. The AAA Similarity Postulate
If three angles of one triangle are
congruent to three angle of
another triangle, then the two
triangles are similar.

39. The AAA Similarity Postulate
If ∠𝐴 ≅ ∠𝐷, 𝑎𝑛𝑑∠𝐵 ≅ ∠𝐸, ∠𝐶 ≅ ∠𝐹.
Then ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹.

40. The AA Similarity Theorem
If ∠𝐴 ≅ ∠𝐷, 𝑎𝑛𝑑∠𝐵 ≅ ∠𝐸.
Then ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹.
If two angles of one triangle are congruent with the
corresponding two angles of another triangle, the two
triangles are similar.

41. Example 1
RI II NO, RI =8, RB=3x+4,ON=16, and OB=x+18
Find a. RB b. OB Ans. x=2 RB=10 OB=20

42. The SAS Similarity Theorem
If two sides of one triangle are
proportional to the corresponding
two sides of another triangle and
their respective included angles
are congruent, then the triangles
are similar.

43. The SAS Similarity Theorem
If
𝐴𝐵
𝐷𝐸
=
𝐴𝐶
𝐷𝐹
𝑎𝑛𝑑 ∠𝐴 ≅ ∠𝐷,
𝑇ℎ𝑒𝑛 ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹

44. Example 2
Are the two triangles similar? Justify your answer.

45. Are the two triangles similar? Justify your answer.

46. The SSS Similarity Theorem
If the sides of one triangle are
proportional to the corresponding
sides of a second triangle, then
the triangles are similar.

47. Exercises:
Each pair of triangles is similar. By which test can they
be proved to be similar ?
(a) (b)
(c)

48. Are the two triangles similar?
Justify your answer.

49. Are the two triangles similar?
Justify your answer.

50. Similar right triangles
The L-L Similarity Theorem
If the legs of a right triangle are
proportional to the corresponding
legs of another right triangle, the
right triangles are similar.

51. The L-L Similarity Theorem
If ∠𝐶 𝑎𝑛𝑑∠𝐹 𝑎𝑟𝑒 𝑟𝑖𝑔ℎ𝑡 𝑎𝑛𝑔𝑙𝑒𝑠 𝑎𝑛𝑑
𝐴𝐶
𝐵𝐶
=
𝐷𝐹
𝐸𝐹
𝑇ℎ𝑒𝑛 ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹

52. Are the two triangles similar?
Justify your answer.

53. Similar right triangles
The H-L Similarity Theorem
If the hypotenuse and a leg of
a right triangle are proportional to
the corresponding hypotenuse
and leg of another right triangle,
then the right triangles are
similar.

54. The H-L Similarity Theorem
If ∠𝐶 𝑎𝑛𝑑∠𝐹 𝑎𝑟𝑒 𝑟𝑖𝑔ℎ𝑡 𝑎𝑛𝑔𝑙𝑒𝑠 𝑎𝑛𝑑
𝐴𝐵
𝐷𝐸
=
𝐴𝐶
𝐷𝐹
𝑇ℎ𝑒𝑛 ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹

55. Example 3:
In the figure UA ⊥ 𝐴𝑀,
𝑀𝐸 ⊥ 𝐸𝑅, 𝑈𝐴 = 24,
𝐴𝑀 = 10, 𝑅𝐸 = 5𝑥 + 2,
𝑎𝑛𝑑 𝐸𝑀 = 𝑥 + 3.
𝐷𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑒 𝑥 𝑠𝑜 𝑡ℎ𝑎𝑡
∆𝑈𝐴𝑀~∆𝑅𝐸𝑀.

56. 5.7 Properties of Similar
triangles
O Perimeters of similar
triangles: Perimeters of similar triangles
are in the same ratio as their
corresponding sides and this ratio is
called the scale factor.
O In figure 5.6 there are two similar
triangles DLMN and DPQR.

57. 5.7 Properties of Similar
triangles
This ratio is called the scale factor.

58. 5.7 Properties of Similar
triangles
Perimeter of D LMN = 8 + 7 + 10 = 25
Perimeter of D PQR = 6 + 5.25 + 7.5 = 18.75
Thus, the perimeters of two similar triangles
are in the ratio of their scale factor.

59. 5.7 Properties of Similar
triangles
O Areas of similar triangles: The ratio of
the areas of two similar triangles is equal
to the ratio of the squares of the
corresponding sides, i.e. the square of the
scale factor.
Figure 5.7

60. 5.7 Properties of Similar
triangles
DABC ~ DPQR
O To prove that
O Draw perpendicular from A and P to meet
seg.BC and seg.QR at D and S
respectively.
O Since DABC ~ DPQR
Figure 5.7

61. 5.7 Properties of Similar
triangles
O also ∠B ≅ ∠Q
O In DABD and DPQS
O also ∠B ≅ ∠Q and ∠ADB ≅ ∠PSQ
O therefore DABD ~ DPQS by A A test.
Figure 5.7

62. 5.7 Properties of Similar
triangles
Thus the areas of two similar triangles are in the same
ratio as the square of their scale factors.

63. 5.7 Properties of Similar
triangles
O Example 1
O In a trapezium ABCD, side AB||CD. The
diagonals AC and BD cut each other at M.
O Prove that

64. 5.7 Properties of Similar
triangles
O Solution:
O To Prove that
O Consider DAMB and DCMD.
O ∠AMB ≅ ∠CMD, vertical angles
O ∠BAM ≅ ∠DCM alternate angles
O Therefore By AA test DAMB ~ DCMD
O thus,

65. Exercises:
O 1. Areas of two similar triangles are 144
sq.cm. and 81 sq.cm. If one side of the
first triangle is 6 cm then find the
corresponding side of the second triangle.
O 2. The side of an equilateral triangle ABC
is 5 cm. Find the length of the side of
another equilateral DPQR whose area is
four times area of DABC.

66. Exercises:
O 3. The corresponding sides of two similar
triangles are 4 cm and 6 cm. Find the ratio
of the areas of the triangles.
O 4. DABC ~ DPQR such that
l(seg.AB) : l(seg.PQ) that is 8 : 6. If area
of D ABC is 48 sq.cm what is the area of
the smaller triangle.

67.  end 
@Reylkastro2
@reylkastro