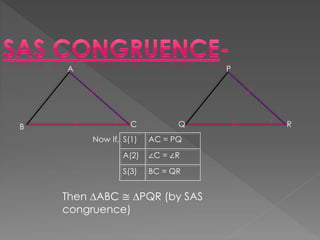
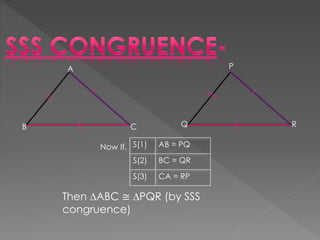
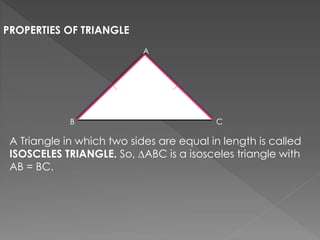
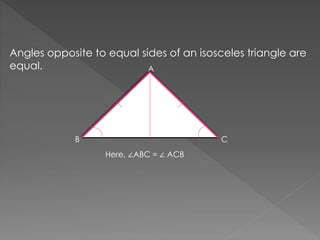
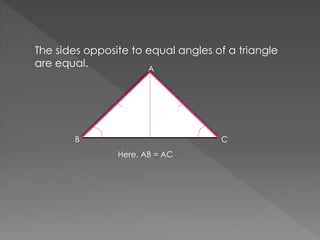
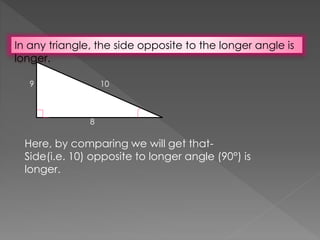
Triangles are congruent if they have the same three sides and three angles. Congruence can be proven using various criteria: SAS (side-angle-side), ASA (angle-side-angle), SSS (side-side-side), RHS (right angle-hypotenuse-side). Properties of triangles include: angles opposite equal sides of an isosceles triangle are equal; sides opposite equal angles are equal; the angle opposite the longer side is larger; the side opposite the longer angle is longer; the sum of any two sides is greater than the third side.