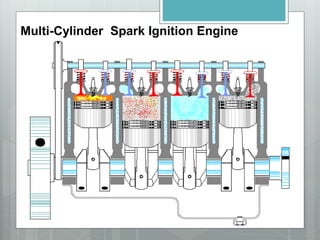
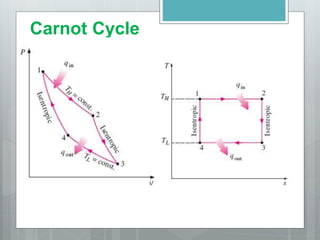
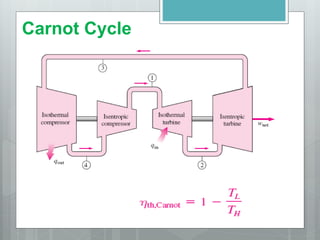
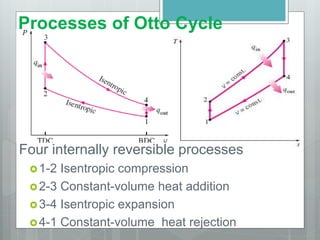
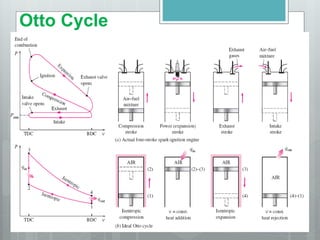
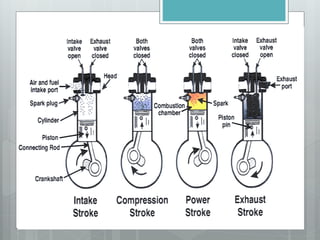
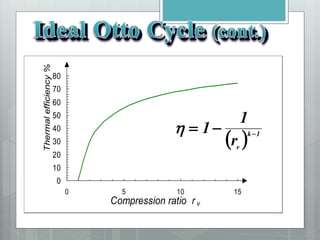
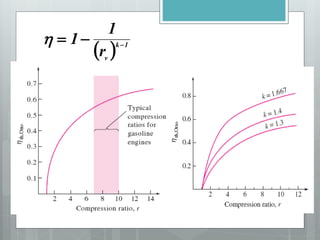
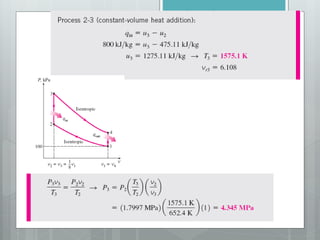
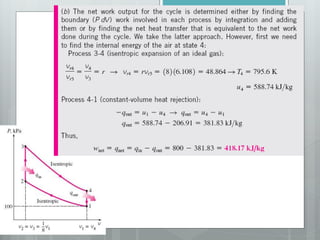
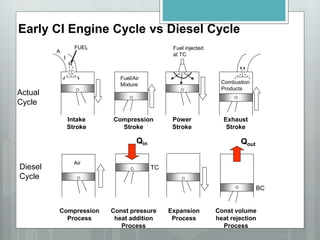
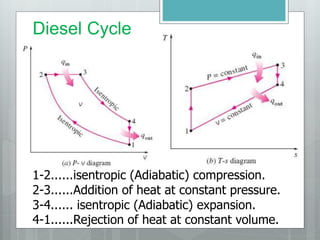
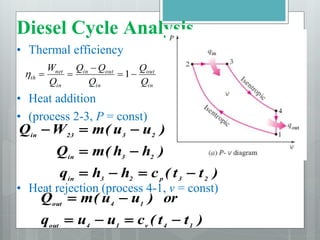
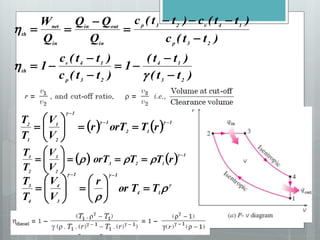
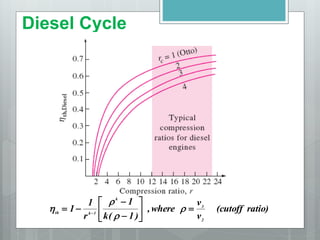
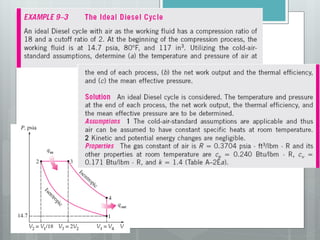
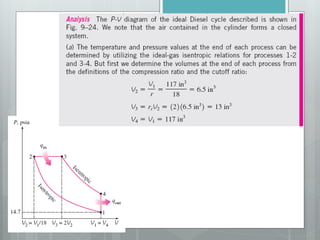
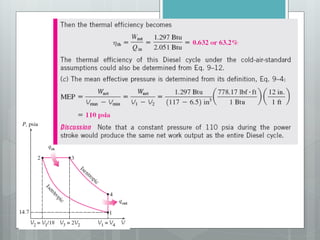
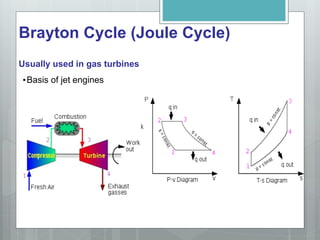
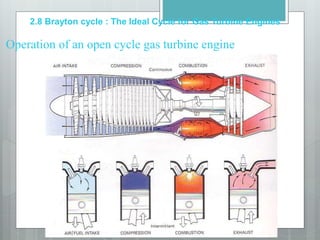
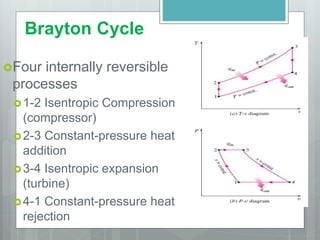
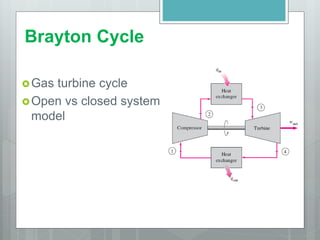
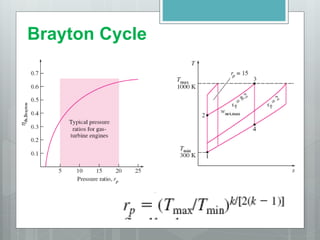
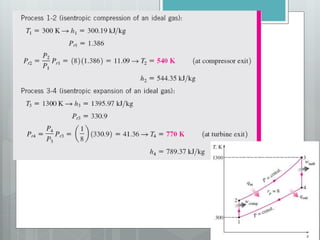
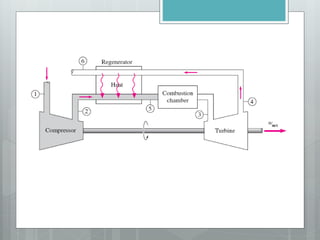
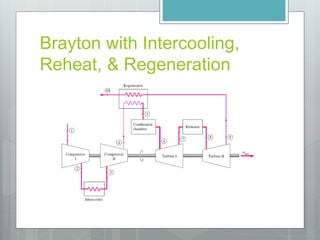
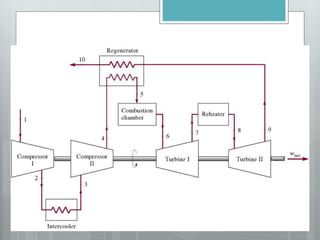
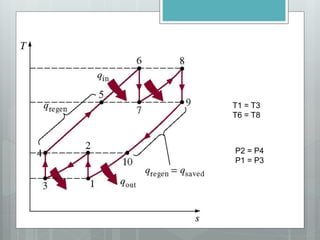
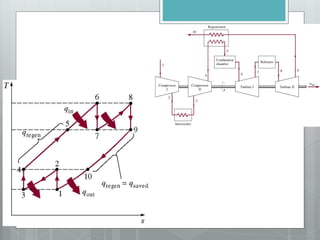
This document describes several gas power cycles including ideal cycles like the Otto cycle, Diesel cycle, and Brayton cycle as well as actual engine cycles. It provides details on the assumptions and processes of each ideal cycle. The Otto cycle involves four internally reversible processes: isentropic compression, constant-volume heat addition, isentropic expansion, and constant-volume heat rejection. The Diesel cycle also involves four internally reversible processes but with compression ignition. The Brayton cycle is typically used in gas turbines and involves isentropic compression, constant-pressure heat addition, isentropic expansion, and constant-pressure heat rejection. Regeneration and intercooling can improve the efficiency of actual cycles.

1. Gas Power Cycles

2. Multi-Cylinder Spark Ignition Engine

3. Power Cycles
Ideal Cycles, Internal Combustion
Otto cycle, spark ignition
Diesel cycle, compression ignition
Brayton cycles
Combined cycle

4. Ideal Cycles Assumptions
Air is the working fluid, circulated in a closed loop,
is an ideal gas
exhaust and air intake are substituted with heat
transfer from the system to the surroundings
combustion is replaced by heat transfer from an
external source to the system
all processes are internally reversible.
gas specific heat is constant
Cycle does not involve any friction
Pipes connecting components have no heat loss
Neglecting changes in kinetic and potential energy

5. Carnot Cycle

6. Carnot Cycle

7. Otto Cycle
Nicolaus August Otto the inventor of
the four-stroke cycle was born on
14th June 1831 in Germany. In
1862 he began first experiments with
four-strokes engines. The first four-
stroke engines is shown. He died on
26th January 1891 in Cologne

8. • Bottom-dead center (BDC) –
• piston position where volume is maximum
• Top-dead center (TDC) –
• piston position where volume is minimum
• Clearance volume –
• minimum cylinder volume (VTDC = V2)
• Compression ratio (r)
• Displacement volume
2
1
2
1
min
max
v
v
V
V
V
V
V
V
r
TDC
BDC




2
1 V
V
V
V
V TDC
BDC
disp 



Engine Terms

9. Engine Terms
Mean effective
pressure (MEP)
disp
net
V
W
MEP 

10. Processes of Otto Cycle
Four internally reversible processes
1-2 Isentropic compression
2-3 Constant-volume heat addition
3-4 Isentropic expansion
4-1 Constant-volume heat rejection

11. Otto Cycle

13. Ideal Otto Cycle (cont.)
1
1
2
2
3
2
1
4
1
V
V
1
)
1
T
/
T
(
T
)
1
T
/
T
(
T
1

















 
 
2
3
v
1
4
v
H
L
T
T
mC
T
T
mC
1
Q
Q
1







H
L
H
H
Q
Q
Q
Q
W
input
heat
work
useful 




L
H
Q
Q
W 


14. const
Pvk

k
2
2
k
1
1
v
P
v
P 
4
3
1
k
3
4
1
k
2
1
1
2
T
T
V
V
V
V
T
T





















  k
1
v
k
1
2
1
2
1
r
1
V
V
1
T
T
1

















1
4
2
3
T
T
T
T


15. 0
10
20
30
40
50
60
70
80
0 5 10 15
Compression ratio r v
Thermal
efficiency
%
  1
k
v
r
1
1 




16.   1
k
v
r
1
1 




22. Diesel Cycle
Rudolf Diesel (1858 – 1913) was born in
Paris in 1858. After graduation he was
employed as a refrigerator engineer. However,
his true love was in engine design. In 1893,
he published a paper describing an engine
with combustion within a cylinder, the
internal combustion engine. In 1894, he filed
for a patent for his new invention, the diesel
engine. He operated his first successful
engine in 1897.

23. Spark or Compression Ignition
 Spark (Otto), air-fuel mixture
compressed (constant-volume
heat addition)
 Compression (Diesel), air
compressed, then fuel added
(constant-pressure heat
addition)

24. Early CI Engine Cycle vs Diesel Cycle
A
I
R
Combustion
Products
Fuel injected
at TC
Intake
Stroke
FUEL
Fuel/Air
Mixture
Air
TC
BC
Compression
Stroke
Power
Stroke
Exhaust
Stroke
Qin Qout
Compression
Process
Const pressure
heat addition
Process
Expansion
Process
Const volume
heat rejection
Process
Actual
Cycle
Diesel
Cycle

25. Diesel Cycle
1-2......isentropic (Adiabatic) compression.
2-3......Addition of heat at constant pressure.
3-4...... isentropic (Adiabatic) expansion.
4-1......Rejection of heat at constant volume.

26. Diesel Cycle Analysis
• Thermal efficiency
• Heat addition
• (process 2-3, P = const)
• Heat rejection (process 4-1, v = const)
in
out
in
out
in
in
net
th
Q
Q
Q
Q
Q
Q
W




 1

)
t
t
(
c
h
h
q
)
h
h
(
m
Q
)
u
u
(
m
W
Q
2
3
p
2
3
in
2
3
in
2
3
23
in









)
t
t
(
c
u
u
q
or
)
u
u
(
m
Q
1
4
v
1
4
out
1
4
out







27. )
t
t
(
)
t
t
(
1
)
t
t
(
c
)
t
t
(
c
1
)
t
t
(
c
)
t
t
(
c
)
t
t
(
c
Q
Q
Q
Q
W
2
3
1
4
2
3
p
1
4
v
th
2
3
p
1
4
v
2
3
p
in
out
in
in
net
th



















    1
1
2
1
1
2
1
1
2
r
T
orT
r
V
V
T
T 
















    1
1
2
3
2
3
2
3
r
T
T
orT
V
V
T
T 




















 1
4
1
1
3
4
4
3
T
T
or
r
V
V
T
T




















28. • Otto Cycle
• Diesel Cycle
v
p
k
th c
c
k
r
/
e
wher
,
1
1 1


 

ratio)
(cutoff
v
v
where
,
)
1
(
k
1
r
1
1
2
3
k
1
k
th










 




Cold-Air Standard Thermal Efficiency

29. Diesel Cycle
ratio)
(cutoff
v
v
where
,
)
1
(
k
1
r
1
1
2
3
k
1
k
th










 





35. Brayton Cycle (Joule Cycle)
Usually used in gas turbines
•Basis of jet engines

36. Operation of an open cycle gas turbine engine
2.8 Brayton cycle : The Ideal Cycle for Gas Turbine Engines

37. Brayton Cycle
Four internally reversible
processes
1-2 Isentropic Compression
(compressor)
2-3 Constant-pressure heat
addition
3-4 Isentropic expansion
(turbine)
4-1 Constant-pressure heat
rejection

38. Brayton Cycle
Gas turbine cycle
Open vs closed system
model

39. Brayton Cycle
 Analyze as steady-flow process
 So
 With cold-air-standard assumptions

40. Brayton Cycle
Since processes 1-2 and 3-4 are
isentropic, P2 = P3 and P4 = P1
where

41. Brayton Cycle

46. Actual Gas-Turbine Cycles
 For actual gas turbines,
compressor and turbine are
not isentropic

47. Regeneration

48. Regeneration
Use heat exchanger
called regenerator
Counter flow
Regenerator Effectiveness
2
4
2
5
max
,
,
h
h
h
h
q
q
regen
act
regen






49. Brayton Cycle
.
•A reheater is a heat exchanger that increases the power output
without increasing the maximum operating temperature but it does not
increase the efficiency of the cycle
•The capital cost to build a reheater alone cannot be justified because
the thermal efficiency does not increase.

50. Brayton with Intercooling,
Reheat, & Regeneration

52. T1 = T3
T6 = T8
P2 = P4
P1 = P3

54. • Decrease the total compression work
• Improve the back work ratio
• If the number of compression and expansion stages is
increased, the ideal turbine cycle with intercooling,
reheating and regeneration approaches the Ericsson cycle

55. 55
Example (9.74): Air enters the compressor of a gas turbine at 100 kPa,
300 K. The air is compressed in two stages to 900 kPa, with intercooling to
300 K between the stages at a pressure of 300 kPa. The turbine inlet
temperature is 1480 K and the expansion occurs in two stages, with reheat
to 1420 K between the stages at a pressure of 300 kPa. The compressor and
turbine stage efficiencies are 84 and 82% respectively, The net power
developed is 1.8 W. Determine
(a) The volumetric flow rate entering the cycle.
(b) The thermal efficiency of the cycle.
(c) The back work ratio.
State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
P (kPa) 100 300 300 900 900 300 300 100
Pr
h (kJ/kg)

56. 56
Example (9.74): The compressor and turbine stage efficiencies are 84 and
82% respectively, The net power developed is 1.8 W. Determine
(a) The thermal efficiency of the cycle.
(b) The back work ratio.
State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
p (kPa) 100 300 300 900 900 300 300 100
pr 1.3860 1.3860 568.8 478.0
h (kJ/kg) 300.19 300.19 1611.79 1539.44
Find state a, Process 1 – a is
1
1
a
raS r
p
p p
p
   158
.
4
100
300
3860
.
1 







From the table haS = 411.26 kJ/kg
Using the isentropic compressor efficiency:
 
 
1
1
h
h
h
h
a
aS




   
kg
kJ
h
h
h
h aS
a 42
.
432
84
.
0
19
.
300
26
.
411
19
.
300
1
1 







Isentropic compression

57. 57
Example (9.74): The compressor and turbine stage efficiencies are 84 and
82% respectively, The net power developed is 1.8 W. Determine
(a) The thermal efficiency of the cycle.
(b) The back work ratio.
State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
P (kPa) 100 300 300 900 900 300 300 100
pr 1.3860 1.3860 568.8 478.0
h (kJ/kg) 300.19 432.42 300.19 1611.79 1539.44
Find state a, Process b – 2 is
From the table h2S = 411.26 kJ/kg
2
2
r S rb
b
p
p p
p
   158
.
4
300
900
3860
.
1 







Using the isentropic compressor efficiency:
 
 
b
b
S
h
h
h
h



2
2

   
kg
kJ
h
h
h
h b
S
b 42
.
432
84
.
0
19
.
300
26
.
411
19
.
300
2
2 







Isentropic compression

58. 58
Example (9.74): The compressor and turbine stage efficiencies are 84 and
82% respectively, The net power developed is 1.8 W. Determine
(a) The thermal efficiency of the cycle.
(b) The back work ratio.
State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
p (kPa) 100 300 300 900 900 300 300 100
pr 1.3860 1.3860 568.8 478.0
h (kJ/kg) 300.19 432.42 300.19 432.42 1611.79 1275.4 1539.44
Find state a, Process 3 – c is
From the table hcS = 1201.5 kJ/kg
3
3
c
rcS r
p
p p
p
   60
.
189
900
300
8
.
568 







Using the isentropic turbine efficiency:
 
 
cS
c
h
h
h
h



3
3

    
kg
kJ
h
h
h
h cS
c 4
.
1275
5
.
1201
79
.
1611
82
.
0
79
.
1611
3
3 





 
Isentropic expansion
State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
p (kPa) 100 300 300 900 900 300 300 100
pr 1.3860 1.3860 568.8 478.0
h (kJ/kg) 300.19 432.42 300.19 432.42 1611.79 1539.44

59. State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
p (kPa) 100 300 300 900 900 300 300 100
pr 1.3860 1.3860 568.8 478.0
h (kJ/kg) 300.19 432.42 300.19 432.42 1611.79 1275.4 1539.44 1216.77
59
Example (9.74): The compressor and turbine stage efficiencies are 84 and
82% respectively, The net power developed is 1.8 W. Determine
State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
p (kPa) 100 300 300 900 900 300 300 100
pr 1.3860 1.3860 568.8 478.0
h (kJ/kg) 300.19 432.42 300.19 432.42 1611.79 1275.4 1539.44
Find state a, Process d – 4 is
From the table h4S = 1145.94 kJ/kg
4
4
r S rd
d
p
p p
p
   33
.
159
300
100
0
.
478 







Using the isentropic turbine efficiency:
 
 
dS
d
h
h
h
h



4
4

    
kg
kJ
h
h
h
h S
d
d 77
.
1216
94
.
1145
44
.
1539
82
.
0
44
.
1539
4
4 





 
Isentropic expansion

60. 60
Example (9.74): The compressor and turbine stage efficiencies are 84 and
82% respectively, The net power developed is 1.8 W. Determine
(a) The thermal efficiency of the cycle.
(b) The back work ratio.
State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
p (kPa) 100 300 300 900 900 300 300 100
pr 1.3860 1.3860 568.8 478.0
h (kJ/kg) 300.19 432.42 300.19 432.42 1611.79 1275.4 1539.44 1216.77
Determine the mass flow rate
1 2 1 2 1.8 /
cycle T T C C
W W W W W kJ s
    
       
 
b
a
d
c
cycle
h
h
h
h
h
h
h
h
m
W







 2
1
4
3


kg
kJ
m
Wcycle
6
.
394



1.8 /
4.562 /
394.6 / 394.6 /
cycle
W kJ s
m kg s
kJ kg kJ kg
  

61. 61
Example (9.74): Air enters the compressor of a gas turbine at 100 kPa,
300 K. The air is compressed in two stages to 900 kPa, with intercooling to
300 K between the stages at a pressure of 300 kPa. The turbine inlet
temperature is 1480 K and the expansion occurs in two stages, with reheat
to 1420 K between the stages at a pressure of 300 kPa. The compressor and
turbine stage efficiencies are 84 and 82% respectively, The net power
developed is 1.8 W. Determine
(a) The volumetric flow rate.
(b) The thermal efficiency of the cycle.
(c) The back work ratio.
State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
p (kPa) 100 300 300 900 900 300 300 100
pr 1.3860 1.3860 568.8 478.0
h (kJ/kg) 300.19 432.42 300.19 432.42 1611.79 1275.4 1539.44 1216.77
s
kg
m 562
.
4


   
  
1
5 2
1
1
0.2870 / 300
V 4.562 /
(10 / )
kJ kg K K
RT
A m kg s
p m

 
 
 
 
 
3
1
V 3.93
m
A
s


62. 62
Example (9.74): Air enters the compressor of a gas turbine at 100 kPa,
300 K. The air is compressed in two stages to 900 kPa, with intercooling to
300 K between the stages at a pressure of 300 kPa. The turbine inlet
temperature is 1480 K and the expansion occurs in two stages, with reheat
to 1420 K between the stages at a pressure of 300 kPa. The compressor and
turbine stage efficiencies are 84 and 82% respectively, The net power
developed is 1.8 W. Determine
(a) The volumetric flow rate.
(b) The thermal efficiency of the cycle.
(c) The back work ratio.
State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
p (kPa) 100 300 300 900 900 300 300 100
pr 1.3860 1.3860 568.8 478.0
h (kJ/kg) 300.19 432.42 300.19 432.42 1611.79 1275.4 1539.44 1216.77
in
cycle
Q
W




   
 
kg
kJ
h
h
h
h
m
Q c
d
in 41
.
1443
2
3 



 

s
kg
m 562
.
4


2734
.
0
41
.
1443
6
.
394



in
cycle
Q
W




63. 63
Example (9.74): Air enters the compressor of a gas turbine at 100 kPa,
300 K. The air is compressed in two stages to 900 kPa, with intercooling to
300 K between the stages at a pressure of 300 kPa. The turbine inlet
temperature is 1480 K and the expansion occurs in two stages, with reheat
to 1420 K between the stages at a pressure of 300 kPa. The compressor and
turbine stage efficiencies are 84 and 82% respectively, The net power
developed is 1.8 W. Determine
(a) The volumetric flow rate.
(b) The thermal efficiency of the cycle.
(c) The back work ratio.
State 1 a b 2 3 c d 4
T (K) 300 300 1480 1420
p (kPa) 100 300 300 900 900 300 300 100
pr 1.3860 1.3860 568.8 478.0
h (kJ/kg) 300.19 432.42 300.19 432.42 1611.79 1275.4 1539.44 1216.77
C
T
W
bwr
W

s
kg
m 562
.
4


   
   
4
3
2
1
h
h
h
h
h
h
h
h
W
W
bwr
d
c
b
a
T
C










401
.
0
06
.
659
46
.
264


bwr