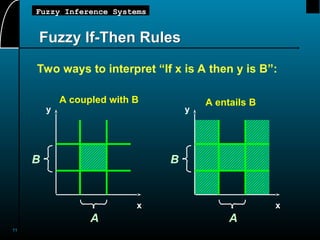
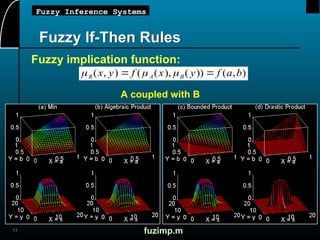
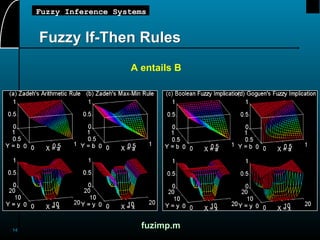
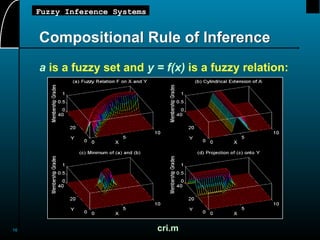
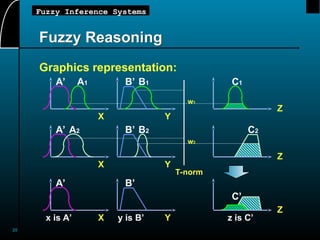
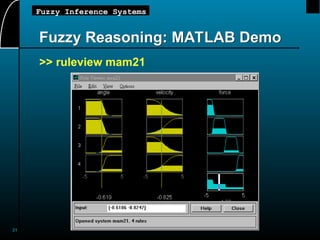
This document provides an overview of fuzzy inference systems (FIS), detailing their structure, functioning, and types including Mamdani, Sugeno, and Tsukamoto systems. It explains concepts such as fuzzy reasoning, linguistic variables, and fuzzy if-then rules, highlighting the importance of fuzzy logic in mapping inputs to outputs based on defined rules. The document also touches on operational aspects of fuzzy inference, including compositional rules and MATLAB demonstrations.




![6
Fuzzy Inference Systems
Max-Star Composition
Max-product composition:
In general, we have max-* composition:
where * is a T-norm operator.
R R
y
R R
x z x y y z
1 2 1 2
( , ) [ ( , ) ( , )]
R R
y
R R
x z x y y z
1 2 1 2
( , ) [ ( , )* ( , )]
](https://image.slidesharecdn.com/ch04-fuzzyinferencesystems-241230065140-ea66ab97/85/Fuzzy-Inference-Systems-by-J-S-Rager-Jan-6-320.jpg)