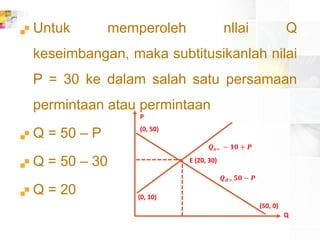
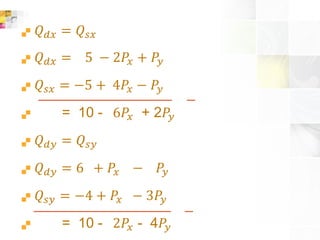Dokumen ini membahas fungsi linear dan persamaan garis, termasuk cara mencari persamaan garis melalui dua titik dan kemiringan garis. Selain itu, terdapat penjelasan mengenai sistem persamaan linier, metode eliminasi, substitusi, serta cara menentukan fungsi permintaan dan penawaran dari suatu produk. Terdapat juga aplikasi grafik dan perhitungan keseimbangan pasar serta harga dan jumlah yang diminta atau ditawarkan.

2.  fungsi linear atau fungsi berderajat satu adalah fungsi
yang pangkat tertinggi dari variabelnya adalah pangkat
satu.
 Bentuk umum persamaan linear adalah
y = a + bx
 a adalah penggal garisnya (intersep) pada sumbu
vertikal - y, sedangkan b adalah koefisien arah atau
lereng garis (slope) yang bersangkutan.

4.  Apabila diketahui dua buah titik A dan B dengan
koordinat masing- masing (x1, y1) dan (x2, y2), maka
rumus persamaan linearnya adalah:
𝒀 − 𝒀 𝟏
𝑿 − 𝑿 𝟏
=
𝒀 𝟐 − 𝒀 𝟏
𝑿 𝟐 − 𝑿 𝟏
y
x
0
A (x1, y1)
B (x2, y2)

5.  Carilah persamaan garis yang melalui titik (3,2) dan (4,6).
 Diketahui; 𝑥1 = 3; 𝑥2 = 4; 𝑦1 = 2; 𝑦2 = 6;
𝒀 − 𝒀 𝟏
𝑿 − 𝑿 𝟏
=
𝒀 𝟐 − 𝒀 𝟏
𝑿 𝟐 − 𝑿 𝟏

𝑌 −2
𝑋 −3
=
6−2
4−3
 𝑦 − 2 =
6−2
4−3
𝑋 − 3
 y – 2 = 4(X - 3)
 y = 4X – 12 + 2
 y = 4X - 10
y = 4X - 10
(0; -10)
(2,5; 0)
Y
X

6. Carilah kemiringan (slope) garis yang telah
ditentukan oleh titik A dan B berikut ini;
 A (3 ; 4), B (4 ; 5)
 A (4 ; 5), B (8 ; 13)
 A (-2 ; 2), B (5 ; 5)
 A (3 ; 2), B (6 ; 8)
 A (-5 ; 2), B (5 ; 6)
 A (3 ; -5), B (8 ; 9)

7.  Apabila diketahui sebuah titik A dengan
koordinat (x1, y1) dan lereng garisnya adalah b,
maka rumus persamaan linearnya adalah:
𝒀 − 𝒀 𝟏 = 𝒎 (𝑿 − 𝑿 𝟏)

8. Carilah persamaan garis yang melalui titik
(6,4) dan kemiringan − 2
3
 Diketahui ; (X,Y) = (6,4) dan m = − 2
3
𝒀 − 𝒀 𝟏 = 𝒎 (𝑿 − 𝑿 𝟏)
 𝑌 − 4 = − 2
3 (𝑋 − 6)
 𝑌 = − 2
3 𝑋 + 4 + 4
 𝑌 = − 2
3 𝑋 + 8

9. Untuk tiap koordinat (X,Y) dan koefisien
kemiringan a berikut ini;
 (2,6); a = 0,4
 (5,8); a = -1,6
 (5,4); a = 0
 (-4,-2); a = 6,2
 (1,8); a = -2,8
 (2,8); a = 4,8

11.  Dua persamaan dengan dua bilangan dapat
diselesaikan dengan cara menghilangkan untuk
sementara (mengeliminasi) salah satu dari bilangan
anu yang ada, sehingga dapat dihitung nilai dari
bilangan yang lain.
5,255
4682
2132
2
1
234
2132







yy-
yx
yx
yx
yx

12. Tentukan nilai X dan Y dari sistem persamaan
linier berikut ini dengan menggunakan metode
eliminasi
 X + Y = 1 ; X - Y = 1
 X + 2Y = 5 ; 2X + 3Y = 8
 2X – 3Y = 13 ; 4X + Y = 15
 2X – Y = 4 ; 5X – Y = 13
 X + Y = 5 ; 2X + 3Y = 12

13.  Dua persamaan dengan dua variabel tak
diketahui dapat diselesaikan dengan cara
menyelesaikan terlebih dahulu sebuah
persamaan untuk salah satu variabel,
kemudian mensubstitusikannya ke dalam
persamaan yang lain.

14. Carilah nilai variable- variable x dan y dari dua
persamaan berikut:
2x + 3y = 21 dan x + 4y = 23
untuk variabel x, diperoleh x = 23-4y
2x + 3y = 21
2(23 – 4y) + 3y = 21
46 – 8y + 3y = 21
46 – 5y = 21, 25 = 5y, y = 5

15. Tentukan nilai X dan Y dari sistem
persamaan linier berikut ini dengan
menggunakan metode subtitusi
 X + 4Y = 3 ; 3X – 2Y = -5
 2X + 3Y = 1 ; X + 2Y = 0
 X + Y = 5; X – Y = 7
 X – 2Y = -7; 5X + 3Y = 20

17.  Suatu produk jika harganya Rp.100,00 akan terjual 10 unit,
dan bila harganya turun menjadi Rp.75,00 akan terjual 20
unit. Tentukanlah fungsi permintannya dan gambarkan
grafiknya?
 Diketahui; 𝑃1 = 100; 𝑃2 = 75; 𝑄1 = 10; 𝑄2 = 20;

𝑄 − 𝑄1
𝑃 − 𝑃1
=
𝑄2− 𝑄1
𝑃2− 𝑃1

𝑄 −10
𝑃 −100
=
20−10
75−100
 (𝑄 − 100) =
10
−25
𝑃 − 100
 (Q – 100) = 40 -
2
5
 Q = 50 – 0,4 P
P
Q
𝑸 𝒅= 𝟓𝟎 − 𝟎, 𝟒𝑷
(0, 125)
(50, 0)

18. Jika fungsi permintaan dari suatu produk adalah P =
1000 – 4Q
 Berapakah harga tertinggi yang dapat dibayarkan oleh
konsumen atas produk tersebut?
 Berapakah jumlah yang diminta jika produk tersebut
gratis
 Gambarkan kurva permintaan tersebut
 Jika harga Rp.500,00, berapkah jumlah yang diminta
konsumen?
 Jika jumlah yang diminta 100 unit, berapakah harganya?

19. Jika harga suatu produk adalah Rp. 500,00, maka
konsumen akan membeli produk tersebut sebanyak 1.500
unit, tetapi jika harganya naik menjadi Rp.600, maka
konsumen hanya membeli 200 unit
 Tentukanlah persamaan dari fungsi permintaan produk
tersebut
 Gambarkan fungsi permintaan dalam bidang cartesius!
 Berpakah harga tertinggi yang mampu dibeli oleh
konsumen?
 Jika jumlah yang diminta oleh konsumen 300 unit,
berpakah harganya?

20. Jika harga suatu produk adalah Rp.500,00, maka jumlah yang akan
terjual sebanyak 60 unit. Bila harga meningkat menjadi Rp.700,00,
maka jumlah produk yang terjual 100 unit. Tunjukanlah fungsi
penawarannya dan gambarkan kurvanya
 Diketahui; 𝑃1 = 500; 𝑃2 = 700; 𝑄1 = 60; 𝑄2 = 100;

𝑄 − 𝑄1
𝑃 − 𝑃1
=
𝑄2− 𝑄1
𝑃2− 𝑃1

𝑄 −60
𝑃 −500
=
100−60
700−500
 (𝑄 − 60) =
40
200
𝑃 − 500
 (Q – 60) =
40
200
(𝑃 − 500)
 Q – 60 = -100 +
1
5
𝑃
 Q = -40 + 0,2P
P
Q
𝑸 𝒔= − 𝟒𝟎 + 𝟎, 𝟐𝑷
(0, 200)
(60, 500)

21. Jika fungsi penawaran dari suatu produk adalah
Q = 2P – 100
 Berapakah harga terendah yang dapat dijual
oleh produsen atas produk tersebut?
 Berapakah jumlah yang diminta jika produk P =
150
 Gambarkan kurva penawaran tersebut

22. Jika fungsi penawaran dari suatu produk adalah P = 5Q +
3000
 Berapakah harga terendah yang dapat dijual oleh
produsen atas produk tersebut?
 Berapakah jumlah yang diminta jika produk P = 8000
 Jika jumlah yang diminta berubah 1 unit, maka
berapakah perubahan harganya?
 Jika harga naik Rp.1.000, berapakah kenaikan jumlah
yang ditawarkan?
 Gambarkan kurva penawarannya

23. Fungsi permintaan dan fungsi penawaran dari suatu barang
ditunjukkan oleh persamaan berikut; 𝑄 𝑑 = 50 − 𝑃; 𝑄𝑠 = −10 + 𝑃
 Carilah harga dan jumlah keseimbangan pasar secara aljabar!
 Gambarkan harga dan jumlah keseimbangan pasar tersebut
dalam sebuah grafik!
 𝑄 𝑑 = 𝑄𝑠
 50 – P = =10 + P
 50 + 10 = P + P
 60 = 2P
 P = 30

24.  Untuk memperoleh nllai Q
keseimbangan, maka subtitusikanlah nilai
P = 30 ke dalam salah satu persamaan
permintaan atau permintaan
 Q = 50 – P
 Q = 50 – 30
 Q = 20
P
Q
𝑸 𝒔= − 𝟏𝟎 + 𝑷
(0, 10)
E (20, 30)
(0, 50)
(50, 0)
𝑸 𝒅= 𝟓𝟎 − 𝑷

25. Carilah harga dan jumlah keseimbangan pasar secara
aljabar dan gambarkan keseimbagan pasar tersebut dari
masing – masing pasangan fungsi permintaan dan
penawaran berikut ini;
 𝑃𝑑 = 10 − 2𝑄; 𝑃𝑠 = 𝑄 + 1
 𝑃𝑑 = 15 − 2𝑄; 𝑃𝑠 = 𝑄 + 3
 𝑃𝑑 = 15 − 3𝑄; 𝑃𝑠 = 2𝑄 + 5
 𝑄 𝑑 = 10 − 𝑃; 𝑄𝑠 = 𝑃 − 2
 𝑄 𝑑 = 15 − 3𝑃; 𝑄𝑠 = 2𝑃 − 5
 𝑄 𝑑 = 15 − 𝑃; 𝑄𝑠 = 4𝑃 + 10

26. Fungsi permintaan dan fungsi penawaran
dari dua macam produk yang mempunyai
hubungan subtitusi sebagi berikut;
 𝑄 𝑑𝑥 = 5 − 2𝑃𝑥 + 𝑃𝑦; 𝑄 𝑑𝑦 = 6 + 𝑃𝑥 − 𝑃𝑦
dan
 𝑄𝑠𝑥 = −5 + 4𝑃𝑥 − 𝑃𝑦; 𝑄𝑠𝑦 = −4 + 𝑃𝑥 − 3𝑃𝑦
 Carilah harga keseimbangan pasar?

27.  𝑄 𝑑𝑥 = 𝑄𝑠𝑥
 𝑄 𝑑𝑥 = 5 − 2𝑃𝑥 + 𝑃𝑦
 𝑄𝑠𝑥 = −5 + 4𝑃𝑥 − 𝑃𝑦
 = 10 - 6𝑃𝑥 + 2𝑃𝑦
 𝑄 𝑑𝑦 = 𝑄𝑠𝑦
 𝑄 𝑑𝑦 = 6 + 𝑃𝑥 − 𝑃𝑦
 𝑄𝑠𝑦 = −4 + 𝑃𝑥 − 3𝑃𝑦
 = 10 - 2𝑃𝑥 - 4𝑃𝑦

28.  Persamaan di atas dikerjakan lagi secara eliminasi
 0 = 10 - 6𝑃𝑥 + 2𝑃𝑦 (X2) 0 = 20 - 12𝑃𝑥 + 4𝑃𝑦
 0 = 10 - 2𝑃𝑥 - 4𝑃𝑦 𝑋1 0 = 10 - 2𝑃𝑥 - 4𝑃𝑦 +
 0 = 30 - 10𝑃𝑥 + 0
 10𝑃𝑥 = 30
 𝑃𝑥 = 3
 Substitusikan nilai 𝑃𝑥 = 3 ke dalam salah satu persamaan
 2𝑃𝑦 = 6𝑃𝑥 − 10
 2𝑃𝑦 = 6(3) − 10
 2𝑃𝑦 = 8
 𝑃𝑦 = 4

29.  Setelah mendapatkan nilai 𝑃𝑦 = 4 dan 𝑃𝑥 =
3, subtitusikan pada persamaan awal untuk
memperoleh 𝑄 𝑥 𝑑𝑎𝑛 𝑄 𝑦
 𝑄 𝑥 = 5 − 2 3 + 4 = 3
 𝑄 𝑦 = 6 + 3 – 4 = 5
 Jadi nilai 𝑄 𝑥 = 3; 𝑄 𝑦 = 5; 𝑃𝑥 = 3 𝑑𝑎𝑛 𝑃𝑦 = 4

30. Fungsi permintaan dan fungsi penawaran dari
dua macam produk yang mempunyai
hubungan subtitusi sebagi berikut;
 𝑄 𝑑𝑥 = 25 − 7𝑃𝑥 + 𝑃𝑦; 𝑄 𝑑𝑦 = 13 + 𝑃𝑥 − 𝑃𝑦 dan
 𝑄𝑠𝑥 = −15 + 5𝑃𝑥 − 𝑃𝑦; 𝑄𝑠𝑦 = −7 + 𝑃𝑥 − 5𝑃𝑦
 Carilah harga keseimbangan pasar?