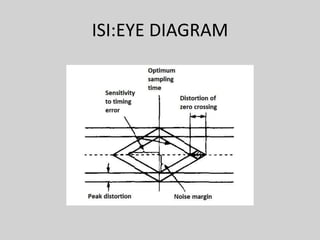
1. The document discusses intersymbol interference (ISI) and various techniques to mitigate its effects, including equalization. ISI occurs when symbols interfere with subsequent symbols due to issues like multipath propagation and bandlimited channels. 2. Eye patterns and diagrams can be used to study ISI and determine the optimal sampling time with the widest eye opening and least sensitivity to timing errors. 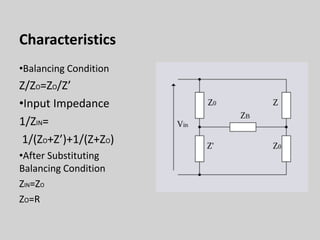3. Equalization techniques aim to reverse channel distortions and make the frequency response flat. Analog techniques include Zobel networks and bridged-T filters, while digital techniques can use linear or decision feedback equalizers. 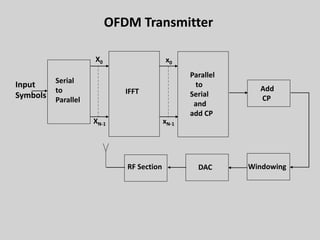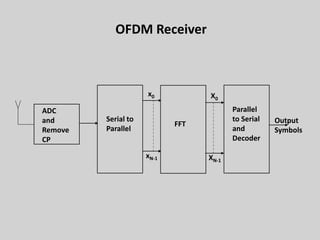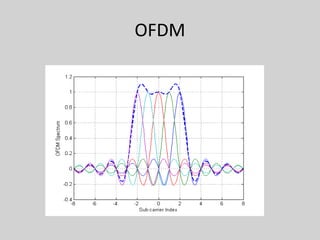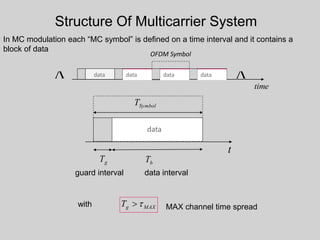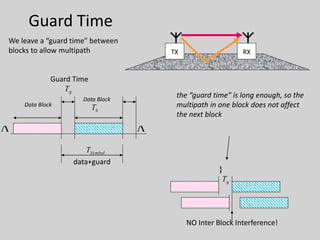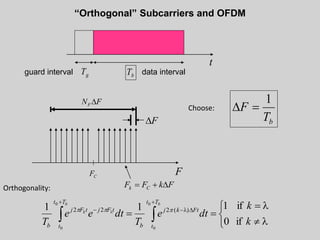4. Orthogonal frequency-division multiplexing (OFDM) is introduced to combat ISI through dividing

1. RECIEVER EQUALIZATION
AND OFDM EQUALIZATION
-VASVI GUPTA

2. ISI (Intersymbol Interference)
• For many physical channels, such as telephone lines, not
only are they band limited, but they also introduce
distortions in their passbands.
• In telecommunication, Intersymbol Interference (ISI) is a
form of distortion of a signal in which one symbol interferes
with subsequent symbols. This is an unwanted
phenomenon as the previous symbols have similar effect
as noise, thus making the communication less reliable.

3. ISI(Intersymbol Interference)
• The spreading of the pulse beyond its allotted time interval
causes it to interfere with neighboring pulses. ISI is usually
caused by multipath propagation.
• The presence of ISI in the system introduces errors in the
decision device at the receiver output
• Therefore, in the design of the transmitting and receiving
filters, the objective is to minimize the effects of ISI, and
thereby deliver the digital data to its destination with the
smallest error rate possible.

4. ISI(Intersymbol Interference)

5. ISI Causes
• Multipath propagation: Propagation of a wireless signal
which suffers reflection and refraction. Due to these effects
signal at receiver are received at different times.
• Bandlimited channels: Another cause of intersymbol
interference is the transmission of a signal through
a bandlimited channel, i.e., one where the frequency
response is zero above a certain frequency (the cutoff
frequency). Passing a signal through such a channel results
in the removal of frequency components above this cutoff
frequency.

6. Studying ISI:EYE PATTERNS
• Apply the received wave to the vertical deflection plates of
an oscilloscope and ALSO apply a sawtooth wave at the
transmitted symbol rate R (R = 1/T) to the horizontal
deflection plates.
• The resulting display is called an eye pattern because of its
resemblance to the human eye
• Following parameters can be analyzed:
 The width of the eye opening defines the time interval
over which the received wave can be sampled without
error from ISI. It is apparent that the preferred time for
sampling is the instant of time at which the eye is open
widest.
 The sensitivity of the system to timing error is determined
by the rate of closure of the eye as the sampling time is
varied.
 The height of the eye opening, at a specified sampling time,
defines the margin over noise.

7. ISI:EYE DIAGRAM

8. Equalization
• Equalization is the reversal of distortion incurred by a signal
transmitted through a channel . Equalizers are used to
render the frequency response—for instance of a
telephone line—flat from end-to-end. When a channel has
been equalized the frequency domain attributes of the
signal at the input are faithfully reproduced at the output.

9. Equalization Techniques
• Equalization may be implemented using
– Analog filters- A traditional technique mainly confined
to fixed channels.
– Digital filters- Have all usual advantage of digital
systems, e.g. flexibility, reliability etc. May be either
fixed or adaptive.

10. Analog telecommunications
1. Zobel networks
• They are a type of filter section based on
the image impedance design principle.
• The impedance would normally be specified
to be constant and purely resistive.
• Zobel networks were formerly widely used
in telecommunications to flatten and widen
the frequency response of copper land lines,
producing a higher-quality line.

11. Characteristics
•Balancing Condition
Z/ZO=ZO/Z’
•Input Impedance
1/ZIN=
1/(ZO+Z’)+1/(Z+ZO)
•After Substituting
Balancing Condition
ZIN=ZO
ZO=R

12. Analog Filters
2. Lattice phase equaliser
• A lattice phase equaliser or lattice filter is an
example of an all-pass filter.
• The lattice filter topology has the particular
property of being a constant-resistance
network and for this reason is often used in
combination with other constant resistance
filters such as bridge-T equalisers.
• The topology of a lattice filter, also called an X-
section is identical to bridge topology.

13. Characteristics
Zo=Z*Z’
Transfer Function
H(w)=(Zo-Z)/(Zo+Z)

14. Analog Filters
3. Bridged T delay equaliser
• The bridged-T delay equaliser is an
electrical all-pass filter circuit utilizing bridged-
T topology whose purpose is to insert an
(ideally) constant delay at all frequencies in
the signal path. It is a class of image filter.

15. Digital Filters
Equalizer types:
• Linear equalizer: processes the incoming signal with
a linear filter
– MMSE equalizer: designs the filter to minimize
E[|e|], where e is the error signal, which is the
filter output minus the transmitted signal.
– Zero forcing equalizer: approximates the inverse of
the channel with a linear filter.
• Decision feedback equalizer: augments a linear
equalizer by adding a filtered version of previous
symbol estimates to the original filter output.

16. Zero-Forcing Equalisers
• Suppose the received pulse is p(t), which suffers ISI
• This signal is sampled at times t=nT to give a digital
signal pn=p(nT)
• We wish to design a digital filter HE(z) which
operates on pn to eliminate ISI
• Zero ISI implies that the filter output is only non-
zero in response to pulse n at sample instant n, i.e.
the filter output is the unit pulse dn in response to
pn

17. Zero-Forcing Equalisers
• Note that the Z transform of dn is equal to 1, so,
)(
1
)(
1)()(
zP
zH
zHzP
E
E


• Now,
......)( 2
2
1
1
0
0  
zpzpzpzP





0i
i
i zp
• So,








0
2
2
1
1
0
0
1
.....
1
)(
1
)(
i
i
i
E
zp
zpzpzpzP
zH
Where pi are the sample
values of the isolated received
pulse

18. MMSE Equaliser
• The MMSE explicitly accounts for the
presence of noise in the system
• Assuming a similar model to that used
previously, then in Z transform notation,
))()()(()( zVzXzHzY E 
HE(z)+
X(z)
V(z)
Y(z)
Where X(z) is the Z transform of the sampled received signal xn, and V(z) is the Z
transform of the noise vn

19. Digital Filters Cont.
• Adaptive equalizer: is typically a linear equalizer or a
DFE. It updates the equalizer parameters (such as the
filter coefficients) as it processes the data. Typically,
it uses the MSE cost function; it assumes that it
makes the correct symbol decisions, and uses its
estimate of the symbols to compute e, which is
defined above.
• Viterbi equalizer: Finds the maximum likelihood (ML)
optimal solution to the equalization problem. Its goal
is to minimize the probability of making an error over
the entire sequence.

20. Cont.
• BCJR equalizer: uses the BCJR algorithm (also called
the Forward-backward algorithm) to find
the solution. Its goal is to minimize the probability
that a given bit was incorrectly estimated.
• Turbo equalizer: applies turbo decoding while
treating the channel as a convolutional code.
• Blind equalizer: estimates the transmitted signal
without knowledge of the channel statistics, using
only knowledge of the transmitted signal's statistics.

21. OFDM(ORTHOGONAL FREQUENCY
DIVISION MULTIPLEXING)

22. Orthogonal Frequency-Division
Multiplexing(OFDM)
• OFDM is a method of encoding digital data on
multiple carrier frequencies.
• OFDM has developed into a popular scheme
for wideband digital communication, used in
applications such as digital television and audio
broadcasting.
• It is a form of signal modulation that divides a
high data rate modulating stream placing them
onto many slowly modulated narrowband close-
spaced subcarriers, and in this way is less
sensitive to frequency selective fading.

23. OFDM

24. How OFDM Works?
• It distributes the data over large number of
carriers that are spaced apart at precise
frequencies. This spacing provides
“orthogonality” in this technique which
prevents the demodulator from seeing
frequencies other than their own.

25. Structure Of Multicarrier System
In MC modulation each “MC symbol” is defined on a time interval and it contains a
block of data
gT bT
SymbolT
data interval
t
guard interval
 
time
OFDM Symbol
data datadatadata
data
MAXgT  MAX channel time spreadwith

26.  
the “guard time” is long enough, so the
multipath in one block does not affect
the next block
Data Block
Data Block
TX RX
Guard Time
We leave a “guard time” between
blocks to allow multipath
gT
Guard Time
bT
SymbolT
data+guard

NO Inter Block Interference!
gT

27. “Orthogonal” Subcarriers and OFDM
gT bT data interval
t
guard interval
bT
F
1






 






k
k
dte
T
dtee
T
bb
k
Tt
t
Ftkj
b
Tt
t
tFjtFj
b if0
if111 0
0
0
0
)(222 
Choose:
Orthogonality:
FCF
F
FkFF Ck 
FN F

28. 28
OFDM and FFT
• Samples of the multicarrier signal can be obtained using
the IFFT of the data symbols - a key issue.
• FFT can be used at the receiver to obtain the data symbols.
• No need for ‘N’ oscillators,filters etc.
• Popularity of OFDM is due to the use of IFFT/FFT which
have efficient implementations.

29. OFDM
• IFFT converts X(k) of length N into a complex time-domain OFDM
signal.
• In order for the IFFT/FFT to create an ISI-free channel, the
channel must appear to provide a circular convolution.
• To mitigate the effects of multipath induced ISI, a guard interval
of G-sample (or cyclic prefix (CP)) is inserted between symbols.
• The length of CP depends on the channel delay spread and is
normally considered to be grater than or equal to the channel
length (impulse response time) and less than symbol duration
29
))}(({)( nkXIFFTnx N

30. Circular Convolution & DFT/IDFT
• Circular convolution:
CSNDSP 2008
30
• Detection of X (knowing H):
(note: ISI free! Just a scaling by H)
• Circular convolution allows DFT!

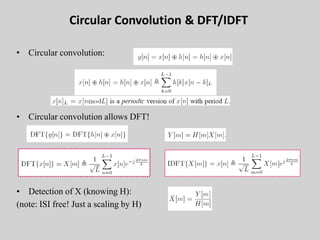
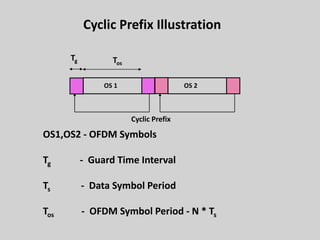
31. OFDM - Cyclic Prefix (CP)
• OFDM signal with CP is x[n]L, and so y[n] = x[n] * h[n].
31

32. • The received OFDM signal propagated through the channel h(n) is given by:
where w[n] is the additive white Gaussian noise and denotes the circular convolution.
CSNDSP 2008 32
][][][.][ nwnhnsnyr 



33. 33
Interpretation of IFFT&FFT
• IFFT at the transmitter & FFT at the receiver
• Data symbols modulate the spectrum and the
time domain symbols are obtained using the IFFT.
• Time domain symbols are then sent on the
channel.
• FFT at the receiver to obtain the data.

34. 34
Cyclic Prefix
• Zeros used in the guard time can alleviate interference
between OFDM symbols (IOSI problem).
• Orthogonality of carriers is lost when multipath channels
are involved.
• Cyclic prefix can restore the orthogonality.

35. 35
Cyclic Prefix
• Convert a linear convolution channel into a circular
convolution channel.
• This restores the orthogonality at the receiver.
• Energy is wasted in the cyclic prefix samples.

36. 36
Cyclic Prefix Illustration
Tos
Tg
Cyclic Prefix
OS 1 OS 2
OS1,OS2 - OFDM Symbols
Tg - Guard Time Interval
Ts - Data Symbol Period
Tos - OFDM Symbol Period - N * Ts

37. 37
Serial
to
Parallel
X0
XN-1
x0
xN-1
IFFT
Parallel
to
Serial
and
add CP
Add
CP
WindowingDACRF Section
Input
Symbols
OFDM Transmitter

38. 38
ADC
and
Remove
CP
Serial to
Parallel
FFT
Parallel
to Serial
and
Decoder
X0
XN-1
x0
xN-1
Output
Symbols
OFDM Receiver

39. OFDM Equalization:
One-Tap Equalizer
In channels impulse responses remain constant
within one OFDM symbol period, the received
signal at each subcarrier takes the form of
Zi,k = Hi,kXi,k + Vi,k
One-tap equalizers restore the transmitted
signal by
Xi,k=Gi,kZi,k
where Gi,k is the equalizer coefficient at the k-th
subcarrier during the i-th symbol.

40. Cont.
• Regardless of noise, the zero-forcing equalizer
simply uses the inverse of the channel
response (Gi,k =Inverse( Hi,k )) and forces the
frequency-selective-faded signals back to flat
faded ones.
• However, it may result in noise enhancement
in the subcarriers that suffer deep fading.

41. MMSE equalizer
• The MMSE equalizer, which tries to minimize
E{|X^i,k-Xi,k|} takes the noise component into
account and equalizes the signal.
• This equalizer has the advantage that the
noise enhancement problem in low-SNR cases
is gone. Also when SNR is high enough, it is
clear that the MMSE equalizer approaches the
zero-forcing equalizer.

42. One-Tap Equalizer Disadvantage
• In fast-fading channels, channel response not only
changes from the previous symbol to the current
symbol, but also varies within one symbol period.
• The fast channel variation within one symbol period
brings about inter-carrier interference, which further
deteriorates the system performance. One-tap
equalizers cannot cope with such situations.
• multiple-tap equalizers which may cancel inter-carrier
interference from adjacent subcarriers are required.

43. REFERENCES
• OFDM Receiver Design for Wireless
Communications-By Tsai
• Introduction To- Sandro Adriano Fassalo
• Wikipedia
• Prof. Aditya K Jagannath Notes: IIT Chennai

44. THANK YOU