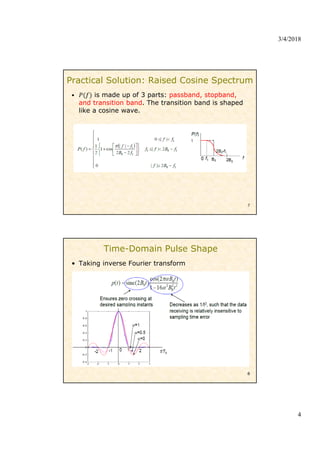
This document provides an overview of digital communication system architecture and techniques for equalization. It discusses: 1) The basic components of a digital communication system including source encoding, channel encoding, modulation, and decoding. 2) Methods for signal design to achieve zero inter-symbol interference (ISI) including the Nyquist criterion and raised cosine pulse shaping. 3) Transmit and receive filter design to compensate for the channel response and minimize noise and ISI. 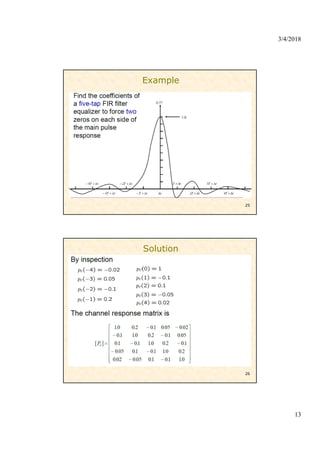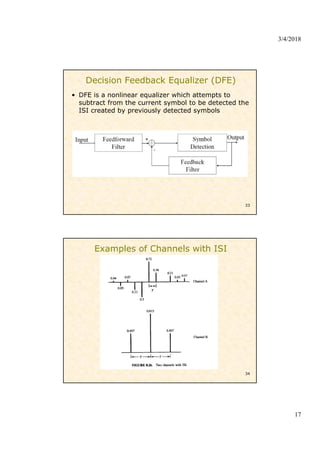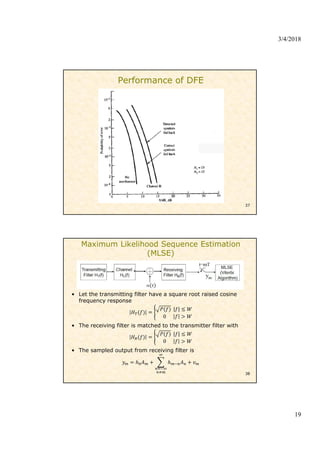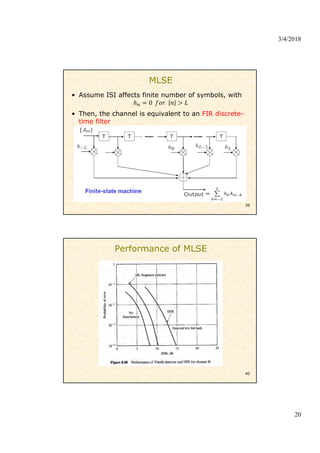4) Equalization techniques used at the receiver including zero-forcing, minimum mean-square error (MMSE), decision feedback equalizers, and maximum likelihood sequence estimation to mitigate ISI caused by multipath channels.

1. 3/4/2018
1
EE140 Introduction to
Communication Systems
Lecture 15
Instructor: Xiliang Luo
ShanghaiTech University, Spring 2018
1
Architecture of a (Digital) Communication System
2
Source
A/D
converter
Source
encoder
Channel
encoder
Modulator
Channel
Detector
Channel
decoder
Source
decoder
D/A
converter
User
Transmitter
Receiver
Absent if
source is
digital
Noise

2. 3/4/2018
2
Contents
• Review: Signal design with zero ISI
• Tx/Rx filter design with channel response
• Equalization
3
Signal Design for Bandlimited Channel
Zero ISI
• Nyquist condition for Zero ISI for pulse shape
1 0
0 0
or ∑ T
• With the above condition, the receiver output
simplifies to
4

3. 3/4/2018
3
Nyquist Condition: Ideal Case
• Nyquist’s first method for eliminating ISI is to use
1 | |
0
/
/
• = Nyquist bandwidth
• The minimum transmission bandwidth for zero ISI.
A channel with bandwidth can support a max.
transmission rate of 2 symbols/sec
5
Achieving Nyquist Condition
• Challenges of designing such or
– ( ) is physically unrealizable due to the abrupt transitions
at
– decays slowly for large t, resulting in little margin of
error in sampling times in the receiver
– This demands accurate sample point timing - a major
challenge in modem / data receiver design
– Inaccuracy in symbol timing is referred to as timing jitter
6

4. 3/4/2018
4
Practical Solution: Raised Cosine Spectrum
• is made up of 3 parts: passband, stopband,
and transition band. The transition band is shaped
like a cosine wave.
7
Time-Domain Pulse Shape
• Taking inverse Fourier transform
8

5. 3/4/2018
5
Contents
• Review: Signal design with zero ISI
• Tx/Rx filter design with channel response
• Equalization
9
Optimum Transmit/Receive Filter
• Recall that when zero-ISI condition is satisfied by
with raised cosine spectrum , then the
sampled output of the receiver filter is
(assume (0)=1)
• Consider binary PAM transmission:
• Variance of noise
with ∗ ∗

10
Error Probability can be minimized through a proper choice
of H f and H f so that / is maximum (assuming H f
fixed and P(f) given)

6. 3/4/2018
6
Optimal Solution
• Compensate the channel distortion equally between
the transmitter and receiver filters
/
/
for
• Then, the transmit signal energy is given by
• Hence
11
By Parseval’s theorem
• Noise variance at the output of the receive filter is
2 2
 ,
Performance loss due to channel distortion
• Special case: 1 for |f|
– This is the ideal case with “flat” fading
– No loss, same as the matched filter receiver for AWGN
channel
12
Optimal Solution (cont’d)

7. 3/4/2018
7
Exercise
• Determine the optimum transmitting and receiving
filters for a binary communications system that
transmits data at a rate R=1/T = 4800 bps over a
channel with a frequency response ;
|f| ≤W where W= 4800 Hz
• The additive noise is zero-mean white Gaussian
with spectral density 2
⁄ 10 Watt/Hz
• Determine the required transmit energy to achieve
10
13
Solution
• Since W = 1/T = 4800, we use a signal pulse with a
raised cosine spectrum and a roll-off factor = 1
• Thus,
1
2
1 cos | | cos
| |
9600
• Therefore
cos
9600
1
4800
, for |f| 4800
• One can now use these filters to determine the
amount of transmit energy required to achieve a
specified error probability
14

8. 3/4/2018
8
Performance with ISI
• If zero-ISI condition is not met, then
• Let
• Then
15
• Often only 2 significant terms are considered.
• Finding the probability of error in this case is quite
difficult. Various approximation can be used
(Gaussian approximation, Chernoff bound, etc.)
• What is the solution?
16
Performance with ISI

9. 3/4/2018
9
Monte Carlo Simulation
17
• If one wants to be within 10% accuracy, how
many independent simulation runs do we need?
• If ~10 (this is typically the case for optical
communication systems), and assume each
simulation run takes 1 msec, how long will the
simulation take?
18
Monte Carlo Simulation (cont’d)

10. 3/4/2018
10
Contents
• Review: Signal design with zero ISI
• Tx/Rx filter design with channel response
• Equalization
19
What is Equalizer
• We have shown that
– By properly designing the transmitting and receiving filters,
one can guarantee zero ISI at sampling instants, thereby
minimizing .
– Appropriate when the channel is precisely known and its
characteristics do not change with time
– In practice, the channel is unknown or time-varying
• Channel equalizer: a receiving filter with adjustable
frequency response to minimize/eliminate inter-
symbol interference
20

11. 3/4/2018
11
Equalizer Configuration
• Overall frequency response
• Nyquist criterion for zero-ISI
• Ideal zero-ISI equalizer is an inverse channel filter
with
∝
1
| | 1/2
21
Linear Transversal Filter
• Finite impulse response (FIR) filter
• are the adjustable 2N+1 equalizer coefficients
• N is sufficiently large to span the length of ISI
22

12. 3/4/2018
12
Zero-Forcing Equalizer
• : received pulse from a channel to be equalized
• ∑
1, 0
0, 1, … ,
To suppose 2N adjacent interference terms
23
Zero-Forcing Equalizer (cont’d)
• Rearrange to matrix form
24

13. 3/4/2018
13
Example
25
Solution
26

14. 3/4/2018
14
Solution
• The inverse of this matrix (e.g by MATLAB)
• Therefore
0.117, 0.158, 0.937, 0.133, 0.091
• Equalized pulse response
• It can be verified that
0 1.0 0, 1, 2
27
Solution
• Note that values of for 2 or 2 are not
zero. For example:
28

15. 3/4/2018
15
Minimum Mean-Square Error Equalizer
• Drawback of ZF equalizer
– Ignores the additive noise
– May even amplify the noise power
• Alternatively,
– Relax zero ISI condition
– Minimize the combined power in the residual ISI and
additive noise at the output of the equalizer
• MMSE equalizer:
– a channel equalizer that is optimized based on the
minimum mean-square error (MMSE) criterion
29
MMSE Criterion
• The output is sampled at :
• Let A = desired equalizer output
≜ Minimum
30

16. 3/4/2018
16
MMSE Criterion (cont’d)
2
where
• MMSE solution is obtained by 0
, 0, 1, … ,
31
E is taken over
and the additive noise
MMSE Equalizer vs. ZF Equalizer
• Both can be obtained by solving similar equations
• ZF equalizer does not consider effects of noise
• MMSE equalizer designed so that mean-square error
(consisting of ISI terms and noise at the equalizer
output) is minimized
• Both equalizers are known as linear equalizers
32

17. 3/4/2018
17
Decision Feedback Equalizer (DFE)
• DFE is a nonlinear equalizer which attempts to
subtract from the current symbol to be detected the
ISI created by previously detected symbols
33
Examples of Channels with ISI
34

18. 3/4/2018
18
Frequency Response
35
Channel B tends to significantly enhance the noise when a
linear equalizer is used (since linear equalizers have to
introduce a large gain to compensate for channel null).
Performance of MMSE Equalizer
36

19. 3/4/2018
19
Performance of DFE
37
Maximum Likelihood Sequence Estimation
(MLSE)
• Let the transmitting filter have a square root raised cosine
frequency response
| |
0
• The receiving filter is matched to the transmitter filter with
| |
0
• The sampled output from receiving filter is
38

20. 3/4/2018
20
MLSE
• Assume ISI affects finite number of symbols, with
0
• Then, the channel is equivalent to an FIR discrete-
time filter
39
Performance of MLSE
40

21. 3/4/2018
21
41
More about Equalization
Thanks for your kind attention!
Questions?
42