The document provides a detailed exploration of band-limited channels and the design of signals for effective transmission with minimal inter-symbol interference (ISI). It discusses various equalization techniques including linear, decision feedback, maximum likelihood sequence estimation (MLSE), turbo, and blind equalization methods, highlighting their principles, advantages, and challenges. Key concepts such as eye diagrams, Nyquist criteria, and the effects of channel characteristics on signal integrity are also examined.

1. REMYA R
M TECH ECE
FIRST YEAR
REG NO: 15304019

2. CONTENTS
 INTRODUCTION
 CHARACTERISATION OF BAND LIMITED SIGNAL
 SIGNAL DESIGN FOR BAND LIMITED SIGNAL
 EYE DIAGRAM
 INTERPRETATION OF EYE DIAGRAM
 DESIGN OF BAND LIMITED SIGNAL FOR NO ISI-
THE NYQUIST CRITERIA

3. CONTENTS
 DESIGN OF BAND LIMITED SIGNAL WITH
CONTROLLED ISI- THE PARTIAL RESPONSE
 LINEAR EQUALIZATION
 DECISION FEEDBACK EQUALIZATION
 MLSE EQUALIZATION
 TURBO EQUALIZATION
 BLIND EQUALIZATION

4. INTRODUCTION
 All physical channels are bandlimited, with C(f) = 0 for |f| > W
 Nondistorting (ideal) channel: |C(f)| = const. for | f | < W and is
linear
 All other channels are nonideal (distort the signal in amplitude,
phase or both)

5. INTRODUCTION
Pulse shaping and equalization is taken into account when the
channel is bandlimited to some specified bandwidth of W Hz
Under this condition, the channel may be modeled as a linear
filter having an equivalent low pass frequency response C(f),
that is zero for lfl >W Hz
 For pulse shaping process, consider the design of the signal
pulse g(t) in a linearly modulated signal represented as
that efficiently utilizes the total available channel bandwidth W

6. INTRODUCTION
 When the channel is ideal for | f | ≤W, a signal pulse can be designed
that allows us to transmit at symbol rates comparable to or exceeding
the channel bandwidth W.
 When the channel is not ideal, signal transmission at a symbol rate
equal to or exceeding W results in inter-symbol interference (ISI)
among a number of 2 adjacent symbols.
 Telephone channels are such channels that are characterized by
as band limited linear filters

7. CHARACTERISATION OF BAND LIMITED CHANNELS
 Consider a band limited channel which is characterized as linear filter
with the low pass frequency response C(f) and the impulse response
as C(t).
Then a signal of the form
]
is transmitted over a bandpass telephone channel, the equivalent low
pass received signal is

8. SIGNAL DESIGN FOR BAND LIMITED SIGNAL
 Consider a lowpass transmitted signal which is common for most of the
modulation techniques is represented as
 Consequently, the received signal can be represented
where
and z(t) reprsents the additive white Guassian noise

9. SIGNAL DESIGN FOR BAND LIMITED SIGNAL
 From the sampled data the required information sequence is
obtained is given by
where
 desired information signal

ISI
additive white gaussian noise variable at the kth
sampling instant

10. SIGNAL DESIGN FOR BAND LIMITED SIGNAL
 The output of the receiving filter is
 After filtering operation, signal is sampled at at times t=kT+ ,
k=0,1,2....

11. EYE DIAGRAM
 The amount of ISI and noise in a digital communication system can
be viewed on an oscilloscope.
 For PAM signals, we can display the received signal y(t) on the
vertical input with the horizontal sweep rate set at 1/T.
 The resulting oscilloscope display is called an eye pattern.
 Eye diagram is a means of evaluating the quality of a received “digital
waveform”
 By quality is meant the ability to correctly recover symbols and
timing
 The received signal could be examined at the input to a digital
receiver or at some stage within the receiver before the decision
stage

12. INTERPRETATION OF EYE DIAGRAM

13.  The effect of ISI is to cause the eye to close
 Thereby reducing the margin for additive noise to cause
errors
 Eye diagram can also give an estimate of achievable
BER
 Check eye diagrams at the end of class for participation
 An eye diagram is a periodic depiction of a digital waveform.
 It helps to visualize the behavior of the system, presence of ISI,
etc.
EYE DIAGRAM

14. DESIGN OF BAND LIMITED SIGNAL FOR NO ISI-
THE NYQUIST CRITERIA
 Assuming that the band-limited channel has ideal frequency
response, i.e., C( f ) = 1 for | f | ≤ W,then the pulse x(t) has a spectral
characteristic
where
The output of the receiver is given by

15. DESIGN OF BAND LIMITED SIGNAL FOR NO ISI-
THE NYQUIST CRITERIA
 The condition for zero ISI is
This condition is also termed as Nyquist criteria for zero ISI or
Nyquist criteria for pulse shaping.
• The necessary and sufficient condition for x(t) to satisfy
is that it’s fourier transform x(f)
satisfy

16. DESIGN OF BAND LIMITED SIGNAL FOR NO ISI-
THE NYQUIST CRITERIA
 Assuming that the band-limited channel has ideal frequencyresponse,
i.e., C( f ) = 1 for | f | ≤ W, then the pulse x(t) has a spectral
characteristic
Where
• We are interested in determining the spectral properties of
the pulse x(t), that results in no inter-symbol interference

17. DESIGN OF BAND LIMITED SIGNAL FOR NO ISI-
THE NYQUIST CRITERIA
 The condition for no ISI
This condition is also termed as Nyquist criteria for zero ISI or
Nyquist criteria for pulse shaping
• The necessary and sufficient condition for x(t) to satisfy
is that it’s fourier transform x(f) satisfies

18. DESIGN OF BAND LIMITED SIGNAL WITH
CONTROLLED ISI-PARTIAL RESPONSE
 The condition of achieving zero ISI , so that the data can be
transferred at maximum possible rate ( R=1/T=2W).
 Instead of achieving zero ISI, this method introduces controlled
amount of ISI in the transmitted signal and counteracts it upon
receiving it.
 The transmit filter is designed to introduce ‘deterministic’ or
‘controlled’ amount of ISI and is counteracted in the receiver side.
 Methods like duobinary signaling, modified duobinary signaling are
employed under this category. The resulting signals are called partial
response signals which are transmitted at Nyquist rate of 2W
symbols/second. This method is also called “Correlative Coding”

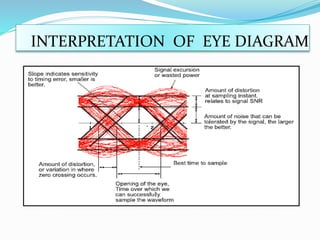
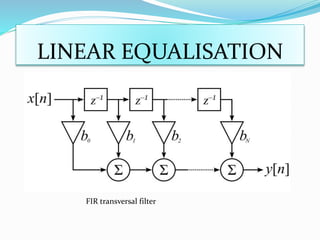
19. LINEAR EQUALISATION
The linear equalizers are simple to implement and:
• Rely on the principle of inverting H (f ).
• Cancel ISI at the cost of possibly enhancing noise (ZFE), or provide
a tradeoff between noise enhancement and ISI removal (MMSE).
In non-blind mode, H (f ) is estimated by feeding an impulse.
 Equalization is performed digitally, so h [n] is what usually matters.
In blind mode, the system uses known training sequences.
heq [n] is implemented as a FIR (finite impulse response) filter.

20. LINEAR EQUALISATION
FIR transversal filter

21. A transveral FIR filter can equalize the worst-case ISI
only when the peak distortion is small.
 In presence of noise, the peak distortion grows.
The MMSE gives the filter coefficients to keep a
minimum mean square error between the output of
the equalizer and the desired signal.
 The MMSE equalizer requires training sequences
(d(t)).
 y(t) and v(t) are signals affected by noise.
LINEAR EQUALIZATION

22.  Linear equalizers are simple to implement, but they
have severe limitations in wireless channels.
 Linear equalizers are not good in compensating for
the appearance of spectral zeros.
 The decision feedback equalizer (DFE) can help in
counteracting these effects.
DECISION FEEDBACK EQUALIZATION

23. DECISION FEEDBACK EQUALIZATION
Structure of a DFE

24.  The DFE works by first estimating the ISI indirectly, in the
feedbackpath.
 The ISI affected signal is reconstructed by using previously
decided symbols, and the result is subtracted from the
output of the feedforward part of the equalizer.
 This feedforward part is responsible for compensating the
remaining ISI.
 The estimated error is used to calculate the forward filter
and the feedback filter coefficients.
 They can be jointly estimated with a minimum mean
square error strategy.
DECISION FEEDBACK EQUALIZATION

25. Advantages
 The system works better in presence of spectral nulls,
because the channel is not inverted.
 It is inherently adaptive.
Drawbacks
• When a symbol is incorrectly decided, this error
propagates during some symbol periods, depending on
the memory of the system.
DECISION FEEDBACK EQUALIZATION

26. MLSE EQUALIZER
 A maximum likelihood sequence estimation (MLSE)
equalizer works over different principles.
 The channel is considered as a system with memory
described by a trellis.
 The state of the system is built by considering the
number of successive symbols matching the length of
the channel response.
 The symbols at the input of the channel drive the
transitions.

27. MLSE EQUALIZER
MLSE equalizer structure for GSM (source:
http://cnx.org/content)

28. MLSE EQUALIZER
 The MLSE equalizer requires training sequences, as in
the case of the DFE or the MMSE.
 It has to build metrics that indicate the likelihood of a
possible transition over the trellis.
 The optimal algorithm to implement the MLSE
criterion is the Viterbi algorithm.

29.  Advantages
 It is optimal from the sequence estimation point of view.
 It can provide the lowest frame error rate.
 Disadvantages
 It is difficult to implement.
 It becomes quickly unfeasible when the channel memory
grows.
 The sequence has to be buffered in blocks, adding delay to
the operation of the system.
MLSE EQUALIZER

30. TURBO EQUALIZATION
Turbo-equalizer principle

31. TURBO EQUALIZATION
 Conventional solutions generally involve both
equalizationand channel coding which are done
separately. In what follows,
 we introduce a new receiver scheme, called a turbo
equalizer,where adaptive equalization and channel
decoding are jointly optimized in order to improve the
global performance
 A turbo equalizer allows the receiver to benefit from
channel decoder gain thanks to an iterative process
applied to the same data block

32. TURBO EQUALIZATION
 In fact, the turbo-equalizer performance depends on
channel selectivity and/or its time variation.
 For a large number of time-invariant channels, the
turbo equalizer succeeds in completely removing the
ISI and exhibits the same performance as the coded
additive white Gaussian noise channels (AWGN).
 For time-varying channels, the turbo equalizer
eliminates ISI and leads to a diversity gain.

33. BLIND EQUALIZATION
 Blind channel equalization is also known as a self-recovering
equalization.
 The objective of blind equalization is to recover the unknown
input sequence to the unknown channel based solely on the
probabilistic and statistical properties of the input sequence.
 The receiver can synchronize to the received signal and to
adjust the equalizer without the training sequence.

34. BLIND EQUALIZATION
• The term blind is used in this equalizer because it performs the
equalization on the data without a reference signal
• Instead, the blind equalizer relies on knowledge of the signal
structure and its statistic to perform the equalization.
 Blind signal is the unknown signal which would be identified in
output signal with accommodated noise signal at receiver.

35. BLIND EQUALIZATION
• Channel equalization uses the idea & knowledge of training
sequences for channel estimation where as Blind channel
equalization doesn’t utilizes the characteristics of training
sequences for frequency and impulse response analysis of
channel.
• Blind Channel Equalization differs from channel equalization and
without knowing the channel characteristics like transfer function
& SNR it efficiently estimate the channel and reduces the ISI by
blind signal separation at receiver side by suppressing noise in
the received signal.

36. THANK YOU