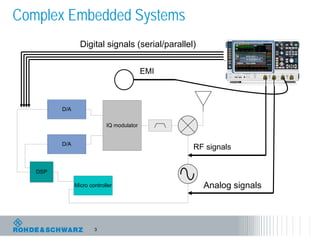
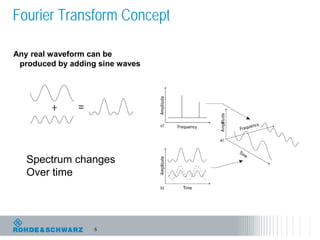
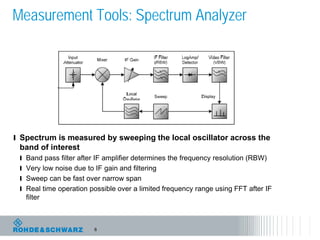
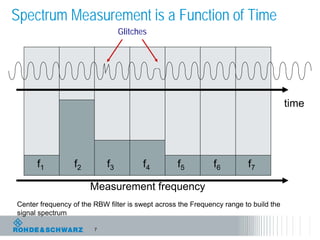
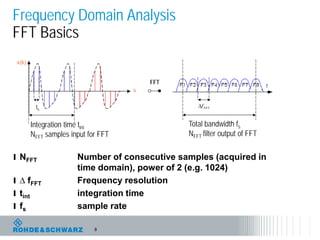
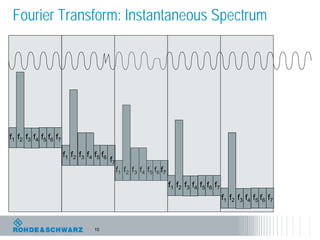
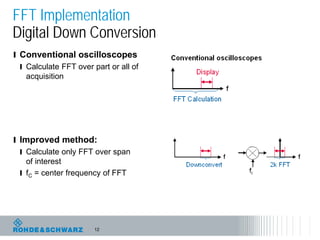
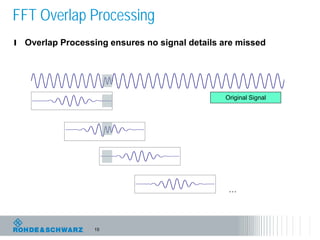
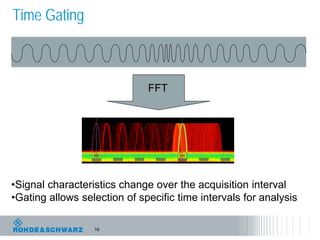
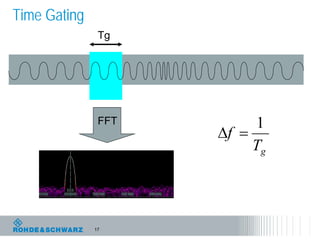
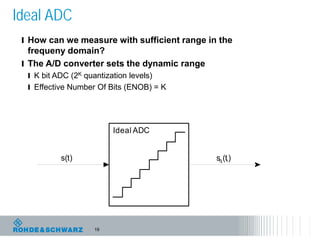
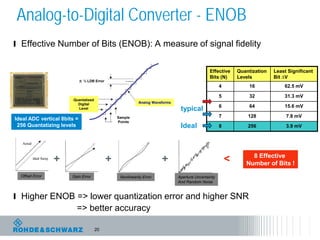
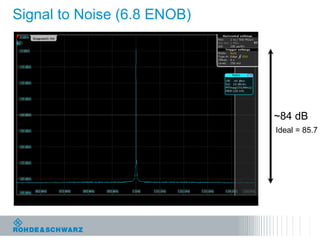
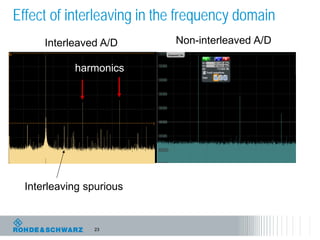
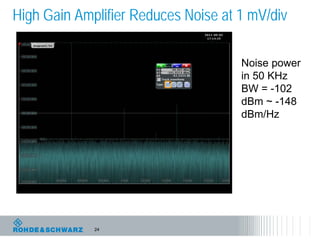
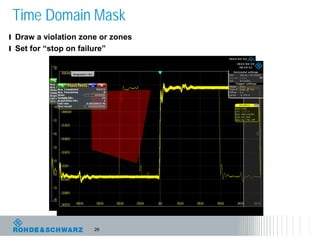
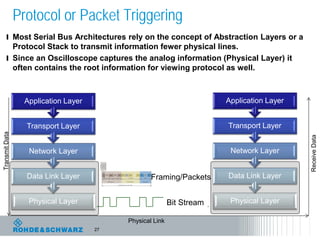
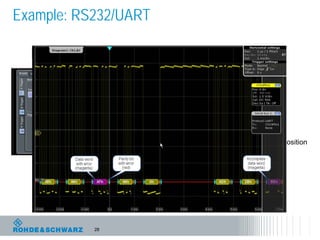
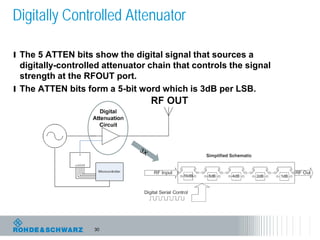
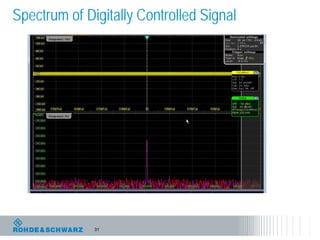
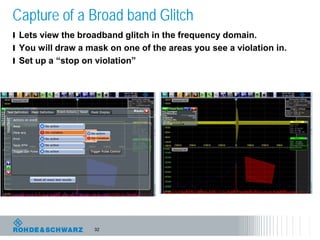
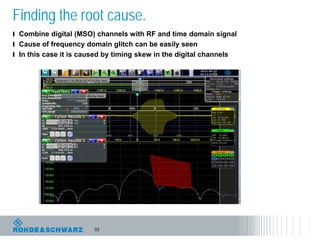
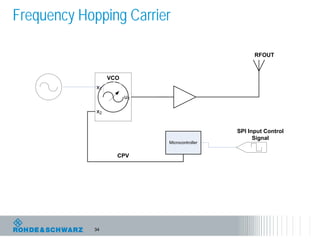
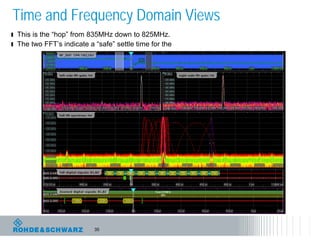
The document discusses the complexities of debugging embedded systems through synchronous time and frequency domain analysis, emphasizing the interdependencies of digital, RF, and analog signals. It covers topics including the Fourier transform, measurement tools like spectrum analyzers, and the importance of effective noise reduction and triggering techniques. Additionally, it highlights the improvements in FFT-based spectrum analysis, dynamic range of ADCs, and real-time analysis in integrated digital and analog environments.

1. Synchronous Time and Frequency
Domain Analysis of Embedded
Systems

2. 2
Agenda
l Complex Embedded Systems
l The Challenge of Debugging Embedded Systems
l Frequency domain analysis
l Time gating
l Dynamic range
l triggering
l Measurement Example: PLL locking
l SPI triggering
l Measuring settling time and transient spectrum

3. 3
Complex Embedded Systems
D/A
D/A
DSP
Micro controller
IQ modulator
Digital signals (serial/parallel)
Analog signals
RF signals
EMI

4. 4
The Challenge of Debugging Embedded Systems
l Baseband digital, RF and analog signals are interdependent
l Feedback control of RF by microcontroller
l Low speed serial busses
l Critical timing relationships
l Interference between RF and digital signals
l EMI
l Analyzing and debugging in the frequency domain
l Frequency domain analysis synchronized with time and digital domains
l Frequency analysis speed
l Sufficient sensitivity in both time and frequency domains
l Triggering ( time, digital and frequency)

5. 5
Fourier Transform Concept
Any real waveform can be
produced by adding sine waves
Spectrum changes
Over time

6. 6
Measurement Tools: Spectrum Analyzer
l Spectrum is measured by sweeping the local oscillator across the
band of interest
l Band pass filter after IF amplifier determines the frequency resolution (RBW)
l Very low noise due to IF gain and filtering
l Sweep can be fast over narrow span
l Real time operation possible over a limited frequency range using FFT after IF
filter

7. 7
Spectrum Measurement is a Function of Time
Glitches
time
f1 f2 f3 f4 f5 f6 f7
Measurement frequency
Center frequency of the RBW filter is swept across the Frequency range to build the
signal spectrum

8. 8
Frequency Domain Analysis
FFT Basics
l NFFT Number of consecutive samples (acquired in
time domain), power of 2 (e.g. 1024)
l ∆ fFFT Frequency resolution
l tint integration time
l fs sample rate
Integration time tint
NFFT samples input for FFT
FFT
Total bandwidth fs
NFFT filter output of FFT
FFTf∆ts

9. 10
f1 f2 f3 f4 f5 f6
Fourier Transform: Instantaneous Spectrum
f1 f2 f3 f4 f5 f6 f7
f1 f2 f3 f4 f5 f6
f7
f1 f2 f3 f4 f5 f6 f7
f1 f2 f3 f4 f5 f6 f7
f7

10. 11
FFT Implementation
Resolution Bandwidth
l Two important FFT rules
l RBW dependent on
l Integration time, e.g. 1 sec => 1 Hz,
100 ms => 10 Hz
l Highest measureable
frequency dependent on
l Sample rate (e.g. fs = 2 GHz => fmax
= 1 GHz)
l Nyquist theorem: fs > 2 fmax
int
max
22 t
Nsf
f FFT
⋅
==
FFTs Ntf =• int

11. 12
FFT Implementation
Digital Down Conversion
l Conventional oscilloscopes
l Calculate FFT over part or all of
acquisition
l Improved method:
l Calculate only FFT over span
of interest
l fC = center frequency of FFT

12. 13
FFT Implementation
Time and Frequency Domains
l 10 us time slice = 1e-6 * 10e9 = 10K samples in FFT
l Using digital down conversion 100 MHz span @ 100 KHz RBW the
FFT length is 1e-6*2e8 = 200 samples
l Multimple FFT's per acquisition e.g. 100 10 us FFT per acquisition
or 200 FFT using 50% overlap
Time line (e.g. 1 ms)
100 KHz RBW
= 20 us
FFT 1 FFT 2 FFT 3 FFT 4
FFT 1
FFT 2
FFT 3
FFT 450% overlapping

13. 14
Tradeoff for Windowing: Missed Signal Events
Original Signal
Signal after Windowing
l All oscilloscope FFT processing uses windowing
l Spectral leakage eliminated
l However, signal events near window edges are attenuated or lost

14. 15
FFT Overlap Processing
l Overlap Processing ensures no signal details are missed
Original Signal
…

15. 16
Time Gating
•Signal characteristics change over the acquisition interval
•Gating allows selection of specific time intervals for analysis
FFT

16. 17
Time Gating
Tg
gT
f
1
=∆
FFT

17. 18
Frequency domain measurement dynamic
range
l Analog to digital conversion (ADC) performance sets the
dynamic range
l Signal to noise ratio (ENOB)
l Frequency domain spurious
l Front-end amplifier gain
l Noise figure and sensitivity

18. 19
Ideal ADC
Ideal ADC
s(t) s (t)q i
l How can we measure with sufficient range in the
frequeny domain?
l The A/D converter sets the dynamic range
l K bit ADC (2K quantization levels)
l Effective Number Of Bits (ENOB) = K

19. 20
Analog-to-Digital Converter - ENOB
l Effective Number of Bits (ENOB): A measure of signal fidelity
l Higher ENOB => lower quantization error and higher SNR
=> better accuracy
Effective
Bits (N)
Quantization
Levels
Least Significant
Bit ∆V
4 16 62.5 mV
5 32 31.3 mV
6 64 15.6 mV
7 128 7.8 mV
8 256 3.9 mV
Offset Error Gain Error Nonlinearity Error Aperture Uncertainty
And Random Noise
+ + +
± ½ LDB Error
Quantatized
Digital
Level
Sample
Points
Analog Waveforms
<
Ideal ADC vertical 8bits =
256 Quantatizing levels
8 Effective
Number of Bits !
Ideal
typical

20. 21
Signal to Noise and ENOB
l What noise level would be observed in the spectrum measured with
100 KHz resolution bandwidth?
l Assume 2 GHz instrument bandwidth with an ideal 8-bit ADC
l SNR = 49.92 dB
l SNRspect = 92.93 dB
l Processing gain = 43.1 dB






∗+=
+∗=
−
≈
51
92
10log10
76.102.6
02.6
76.1
E
E
SNRSNR
BSNR
SNR
B
spect
dB
Displayed noise level is
reduced by the ratio of
full bandwidth to RBW

21. 22
Signal to Noise (6.8 ENOB)
~84 dB
Ideal = 85.7

22. 23
Effect of interleaving in the frequency domain
harmonics
Interleaving spurious
Interleaved A/D Non-interleaved A/D

23. 24
High Gain Amplifier Reduces Noise at 1 mV/div
Noise power
in 50 KHz
BW = -102
dBm ~ -148
dBm/Hz

24. 25
Triggering
l Triggers can be required different “domains”
l Time domain (edge, runt, width, etc.)
l Digital domain (pattern, serial bus)
l Frequency domain (amplitude/frequency mask)
l Sensitivity of time domain triggers
l Matching bandwidth with acquisition for all trigger types
l Noise reduction (filtering, hysteresis)
l Frequency domain triggers
l Processing speed of FFT

25. 26
Time Domain Mask
l Draw a violation zone or zones
l Set for “stop on failure”

26. 27
l Most Serial Bus Architectures rely on the concept of Abstraction Layers or a
Protocol Stack to transmit information fewer physical lines.
l Since an Oscilloscope captures the analog information (Physical Layer) it
often contains the root information for viewing protocol as well.
Protocol or Packet Triggering
Physical Layer
Data Link Layer
Network Layer
Transport Layer
Application Layer
Physical Layer
Data Link Layer
Network Layer
Transport Layer
Application Layer
Bit Stream
TransmitData
ReceiveData
Physical Link
Framing/Packets

27. 28
Example: RS232/UART
Trigger Types:
• Start bit
• Frame start
• Packet start
• A specified symbol
• Parity errors, and breaks
• Frame errors
• Stop errors
• A serial pattern at any or a specified position

28. 29
Frequency Domain Mask
l Mask test on spectrum
l Set for “stop on failure”
Frequency
mask
Gated FFT

29. 30
Digitally Controlled Attenuator
l The 5 ATTEN bits show the digital signal that sources a
digitally-controlled attenuator chain that controls the signal
strength at the RFOUT port.
l The ATTEN bits form a 5-bit word which is 3dB per LSB.

30. 31
Spectrum of Digitally Controlled Signal

31. 32
Capture of a Broad band Glitch
l Lets view the broadband glitch in the frequency domain.
l You will draw a mask on one of the areas you see a violation in.
l Set up a “stop on violation”

32. 33
Finding the root cause.
l Combine digital (MSO) channels with RF and time domain signal
l Cause of frequency domain glitch can be easily seen
l In this case it is caused by timing skew in the digital channels

33. 34
Frequency Hopping Carrier
Microcontroller
SPI Input Control
Signal
u1
x2
x1 * / *
VCO
CPV
RFOUT

34. 35
Time and Frequency Domain Views
ı This is the “hop” from 835MHz down to 825MHz.
ı The two FFT’s indicate a “safe” settle time for the

35. 36
Summary
l FFT based spectrum analysis can be enhanced to enable
time-correlated spectrum analysis
l Improved throughput using digital down conversion
l High dynamic range A/D conversion
l High gain amplifier for small signal measurement
l Real time oscilloscope platform is ideal for digital, time and
frequency analysis
l Synchronized time and frequency domain analysis
l Serial protocol trigger and decode
l Parallel data channels