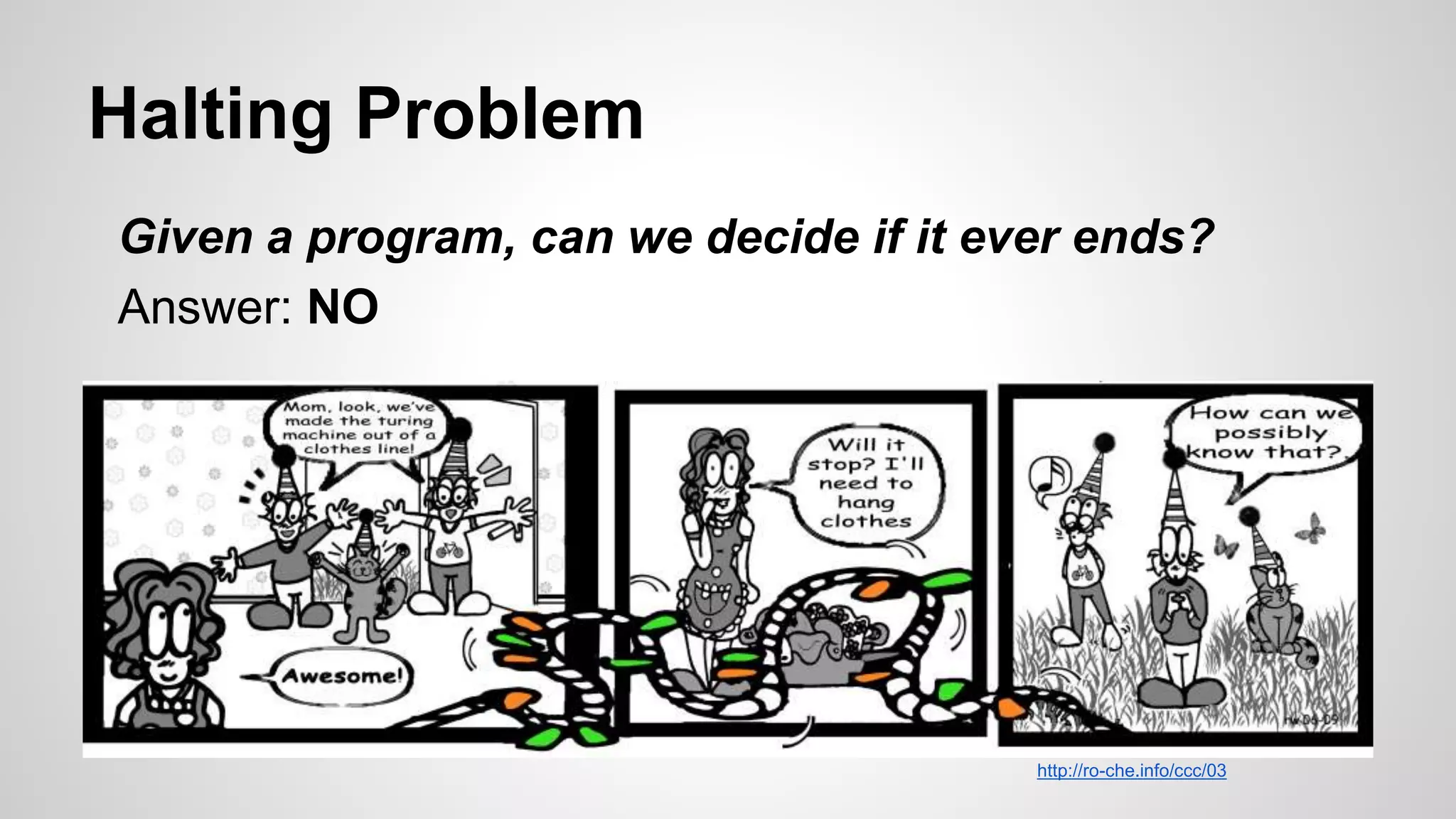
This document provides an overview of topics that will be covered in a course on formal methods in software, including finite state machines, stack machines, specification languages, category theory, logic, and more. It discusses the need for formal methods in safety-critical domains like medical devices and aviation but not for applications like social media. As an example, it walks through a proof of the Euclidean algorithm for finding the greatest common divisor. It also covers important concepts in the field like Gödel's incompleteness theorems, the Entscheidungsproblem, the halting problem, and the Collatz conjecture. Finally, it discusses limitations of formal methods and approaches like unit testing.

1. Formal Methods in
Software
Lecture 1. Introduction
Vlad Patryshev
SCU
2014

2. Content of this course
• FSM, deterministic/non-deterministic; (P/NP); regexp; code sample (the
one-liner), problem with the code; p!=np
• Stack machine, context-free languages; general languages; Turing
machine; some Turing stuff, examples of Turing machine
• Z specification language
• Pi calculus and its fate;
• Monoid, Group, Groupoid, Category, Monomorphisms, Epimorphisms,
Isomorphisms, show it on sets and monoids; Scala (Java) category
• terminal object, initial object; products, unions; show code samples;
equalizers, code samples; notation {x|f(x)==g(x)}; pullbacks, sql
• functors examples (diagrams; product; exponentiations); currying/yoneda
lemma; example with integers/rationals; monad?

3. What you have to know
• first-order logic; quantifiers (see COEN260 slides)
• some set theory; binary relationships, currying;
injection/surjection/bijection (see COEN260 slides)
• some intro to intuitionistic logic (see COEN260 slides)
• javascript or java or scala

4. Formal Methods
• Need them in:
o medical devices
o space
o military
o communications
• Don’t need them in:
o social networks
o ads and sales
o startups

5. Example of Algorithm Proof
Euclidean Algorithm:
Find GCD(a,b), where a and b are two natural numbers.
1. If a < b, use the fact that GCD(a,b)=GCD(b,a)
2. GCD(a,0) = a; done.
3. GCD(a,b) = GCD(a-b,a)
4. Repeat until done.
Proof:
A. Prove that GCD(a,b)=GCD(b,a)
B. Prove that GCD(a,0) = a
C. Prove that GCD(a,b) = GCD(a-b,a)
D. Prove that it takes not more than 2*max(a,b) steps.

6. You are asked to double a cube
Have a cube, V=x3
Build a cube of size 2*V, using a divider and a ruler
Informally: approximate; we only have doubles in Java.
Formally: have to calculate √3(2)
The thing is: You Can’t

7. A similar problem
Need an algorithm to find roots of a 5th degree polynomial
Explanation: 5 roots, S5 is the group of all permutations,
and it cannot be represented via a chain of +/-
symmetries.
x5-x+1 = 0

8. Gödel’s First Theorem
Meaning, if we have a theory T, we can always come up with a statement in T
that cannot be proved.
How?
• enumerate all sentences; then all proofs.
• isProvable(n) ≡ ∃F (n=#(F) ∧ F is provable)
• (diagonal lemma) ∀F ∃p (p ↔ F(#(p))
• how about p ↔ ¬isProvable(#(p))
A theory that contains arithmetics cannot be
at the same time consistent and complete.

9. Entscheidungsproblem
Is there an algorithm that, given a first-order theory, takes a statement
and checks whether the statement is true?
(The essence of the proof of program validity.)
The answer is: NO
Church proved that there is no computable function which decides for two
given λ calculus expressions whether they are equivalent or not.
Turing proved that it reduces to Halting Problem

10. Halting Problem
Given a program, can we decide if it ever ends?
Answer: NO
http://ro-che.info/ccc/03

11. Collatz Conjecture
function(n) {
while (n > 1) {
println(n);
n = n%2==0 ? n/2 : (3*n+1)
}
}
E.g. 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
Will it ever stop?
Nobody Knows.

12. So, what can we do?
• limit ourselves by only provable algorithms
• count on the finiteness of the universe (is it finite?)
• count on the finiteness of time (is it finite?)
• write some unittests and pray (is it a formal method?!)

13. Unittests
• You cannot prove the program is right, but you can find errors
• Can cover main and corner cases
• Can check behavior independently from environment
• Can feel safe doing refactorings
Some people tried to formalize unittest creation (agitar.com) (see e.g. halting
problem)
Question: can you write a unittest for random numbers generator?