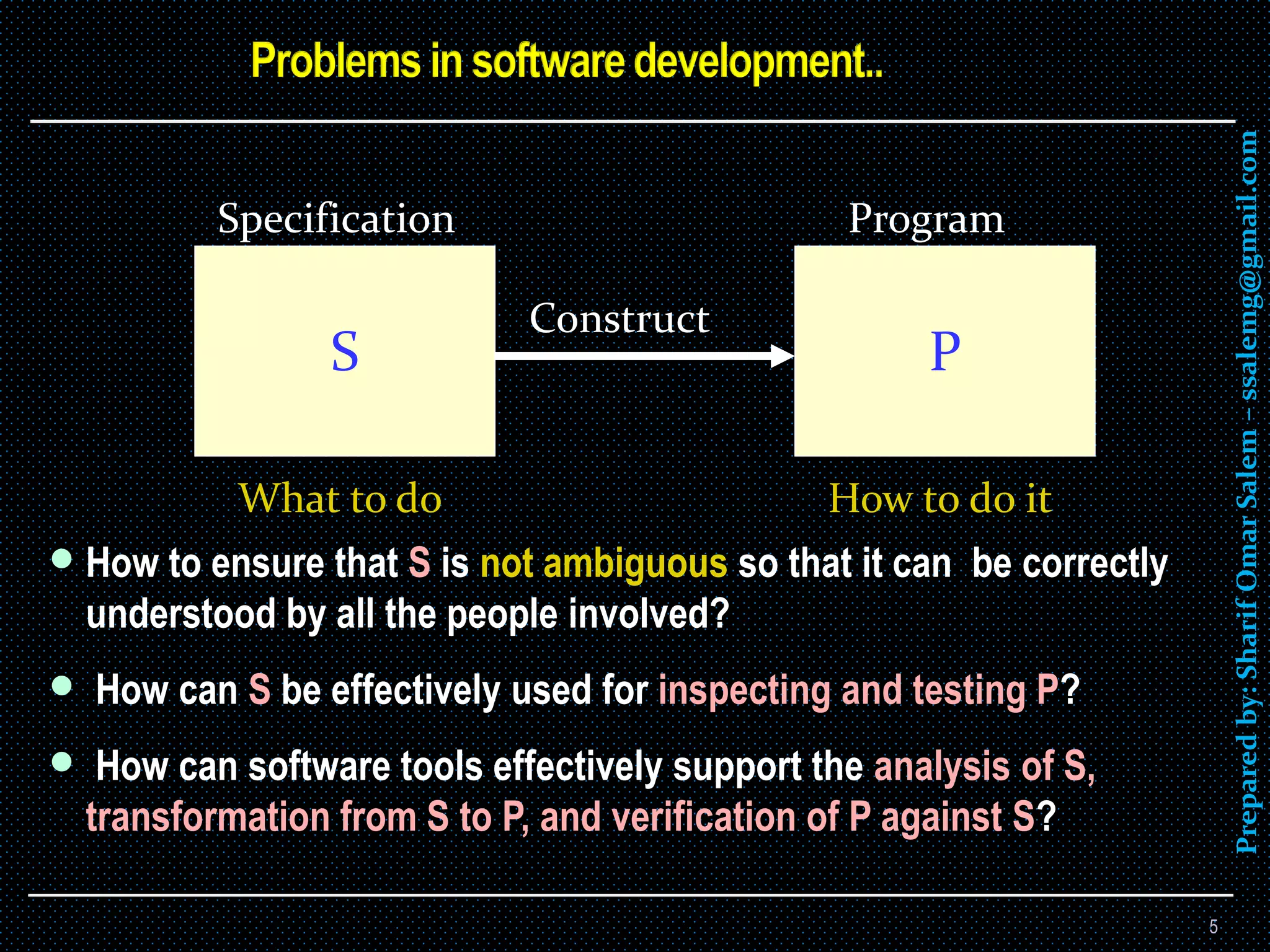
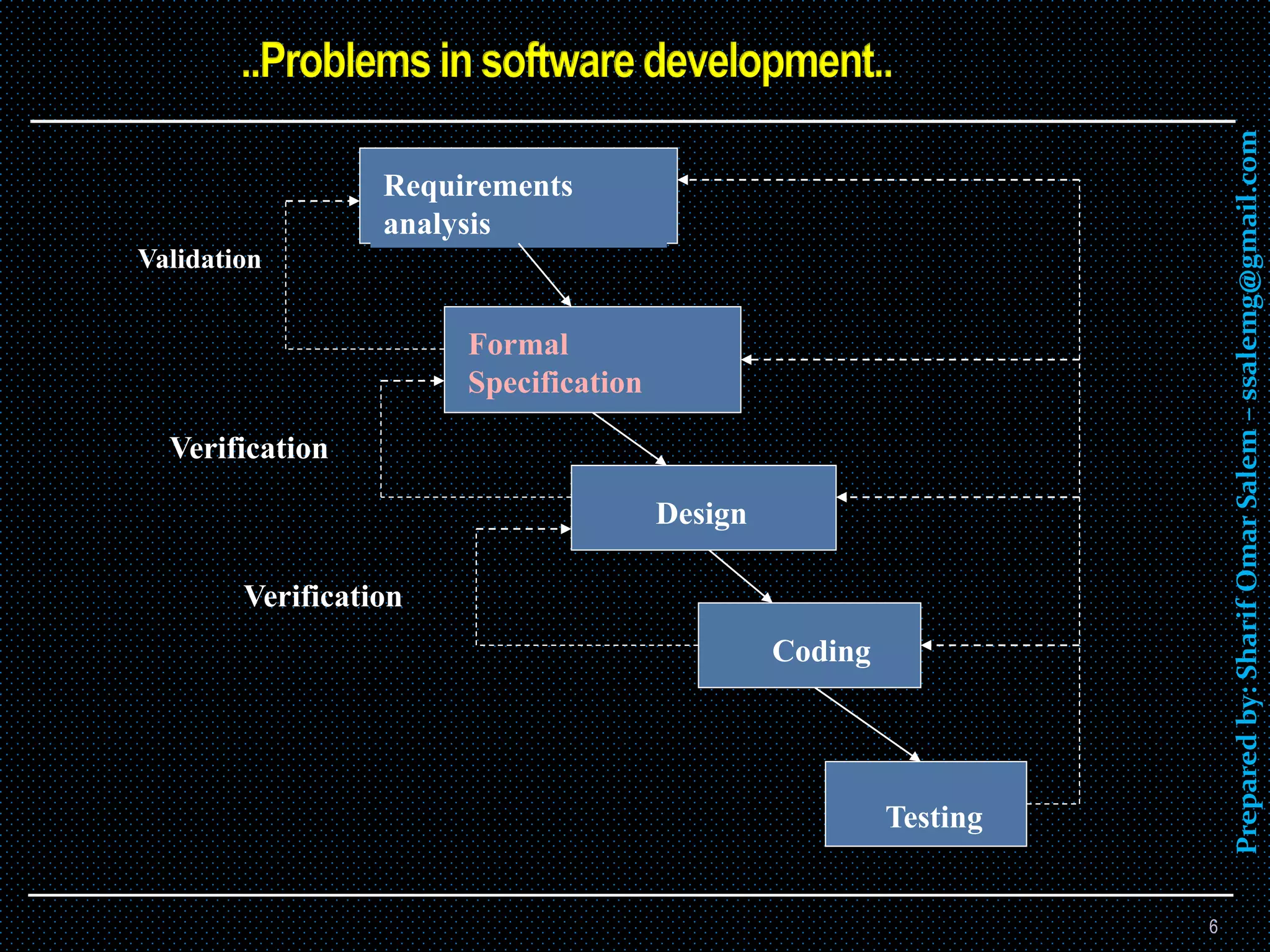
The document discusses formal methods in software engineering, which are mathematical techniques for specifying, developing, and verifying software and hardware systems to ensure reliability and safety. It highlights the significance of formal methods in critical systems, presents different programming paradigms, and provides examples of tools and case studies that demonstrate the application of formal methods. Additionally, it addresses the challenges, benefits, and the evolving nature of formal verification practices in the industry.