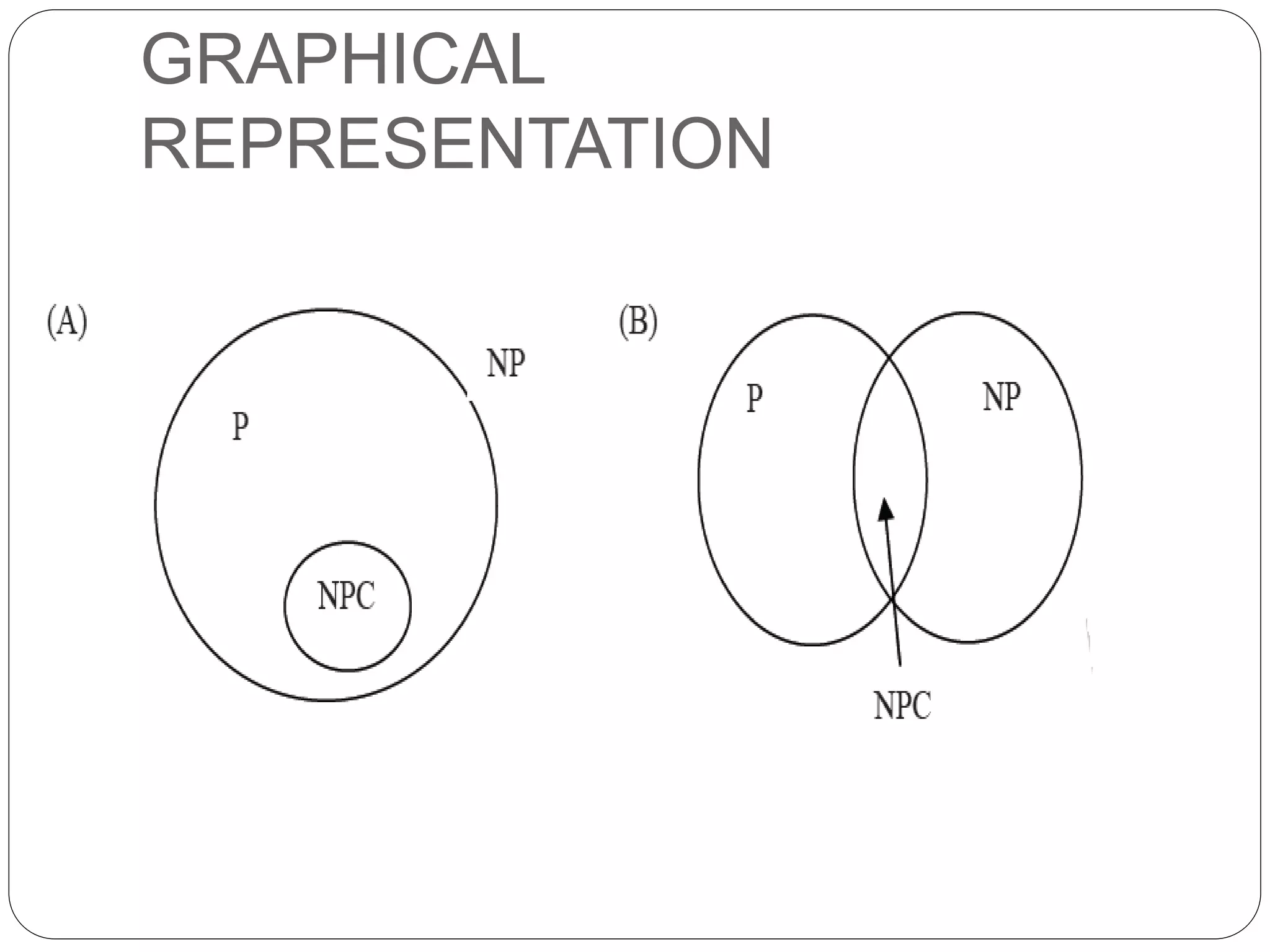
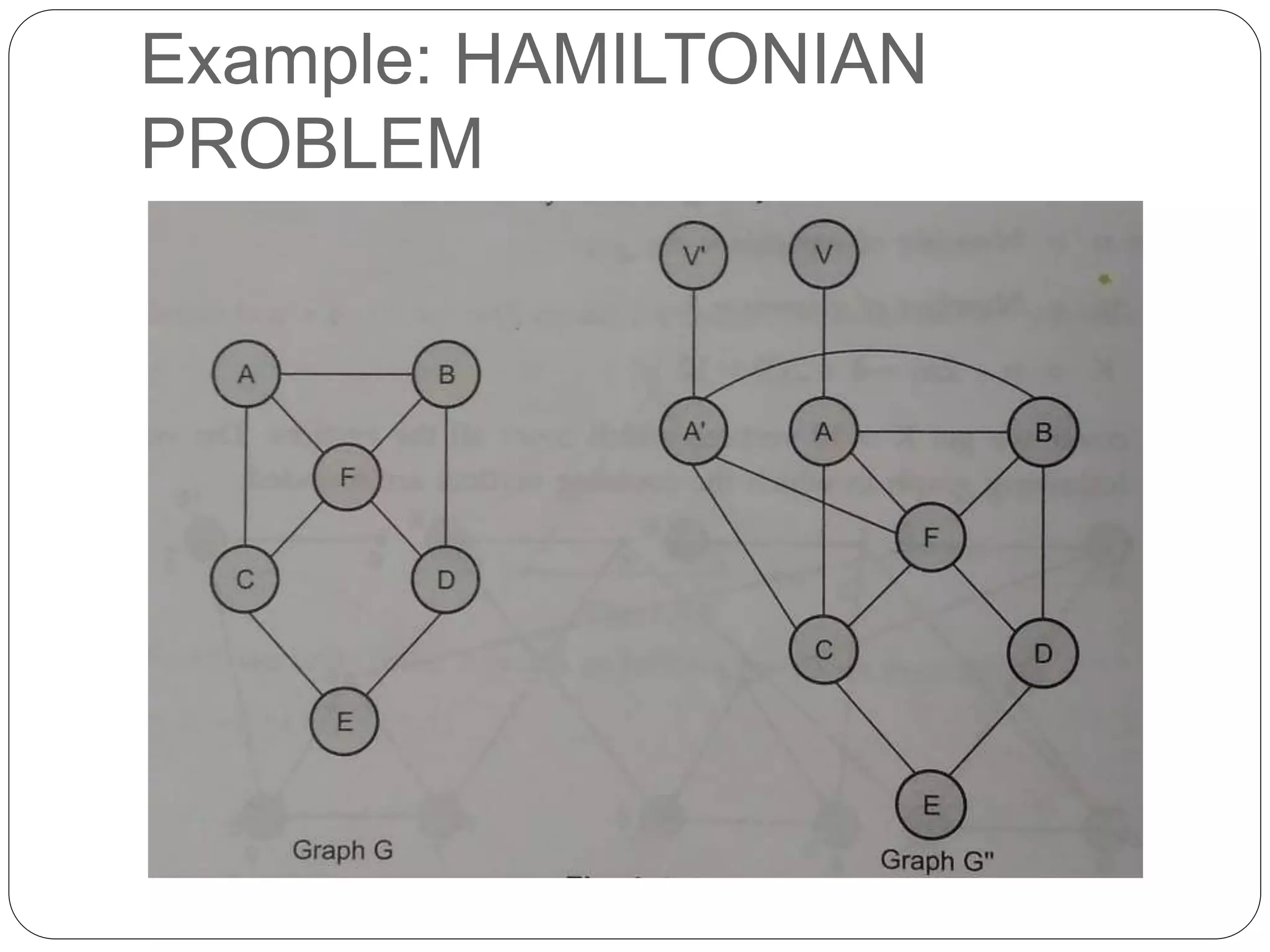
The document summarizes the concepts of P vs NP complexity classes. It states that P problems can be solved in polynomial time, like searching an array, while NP problems are solved in non-deterministic polynomial time, like the knapsack problem. It then defines different types of algorithms and complexity classes. The key classes discussed are P, NP, NP-Complete, and NP-Hard. It provides examples like sorting being in P, while the Hamiltonian problem is NP-Complete. A graphical representation is also included to illustrate the relationships between the complexity classes.

1. Sardar VallabhBhai Patel Institute
Of Technology
 Name- RAJAN
SHAH
 TOPIC- NP
COMPLETENE
SS

2. Classes P & NP
 The problem can be classified into two
groups:
1. The problems that can be solved in
POLYNOMIAL TIME (P)– eg: searching an
element from an array ( O(log(n)))
2. The problems that can be solved in NON-
DETERMINISTIC POLYNOMIAL TIME
(NP)– eg: Knapsack Problem(O(2(n/2))

3. Types of Algorithm
 Decision Algorithm :Any problem for which the
answer is either YES/NO.
 Optimization Algorithm: Any problem that involves
the identification of optimal cost.
 Deterministic Algorithm: An algorithm for which
the same o/p gets generated for given i/p, for a
function. The next state to be followed is fixed. ‘P’
class algorithms are DETERMINISTIC.
 Non Deterministic Algorithm: Algorithm for which
there are more than one paths to follow, due to
which it is difficult to determine which path should
it follow after a particular stage. NP class
problems are NON DETERMINISTIC.

4. P class
 ‘P’ is a complexity class that represents the
set of all decision problems that can be solved
in polynomial time.
 That is, given an instance of the problem, the
answer yes or no can be decided in
polynomial time.
 Examples: Searching an element in an array,
Sorting an array.

5. NP Class
 NP class problems can be are the ones which
can be solved in NON-DETERMINISTIC
POLYNOMIAL TIME.
 It is further divided into: NP COMPLETE and
NP HARD problems.

6. NP COMPLETE PROBLEMS
 NP-Complete is a complexity class which
represents the set of all problems X in NP for
which it is possible to reduce any other NP
problem Y to X in polynomial time.
 Intuitively this means that we can
solve Y quickly if we know how to
solve X quickly.
 Precisely, Y is reducible to X, if there is a
polynomial time algorithm ’f’ to transform
instances ’y’ of Y to instances x = f(y) of X in
polynomial time, with the property that the
answer to ’y’ is yes, if and only if the answer

7. NP HARD PROBLEMS
 These are the problems that are at least as
hard as the NP-complete problems.
 NP-hard problems do not have to be in NP,
and they do not have to be decision problems.
 Consider a problem X is NP-hard, if there is
an NP-complete problem Y, such that Y is
reducible to X in polynomial time.

8.  But since any NP-complete problem can be
reduced to any other NP-complete problem in
polynomial time, all NP-complete problems
can be reduced to any NP-hard problem in
polynomial time.
 Then, if there is a solution to one NP-hard
problem in polynomial time, there is a solution
to all NP problems in polynomial time.

9. GRAPHICAL
REPRESENTATION

10. Non Deterministic Algorithm
 Algorithm in which every operation may not have
unique result, rather there can be specified set of
possibilities for every operation.
 There is no particular rule to make the guess and
it follows two steps:
1. Guessing Stage: Generate an arbitrary string
that can be thought of as a candidate solution
2. Verification Stage: It takes as i/p the candidate
solution and the instance to the problem and
returns YES if the candidate solution represents
actual solution.

11. Example: HAMILTONIAN
PROBLEM

12. Continue
 Acc to the graph G, G” is constructed such that G
contains a Hamiltonian Cycle iff G” contains
Hamiltonian Path.
 Here, Graph G consists Hamiltonian Cycle: A-B-D-E-
C-F-A and G” contains Hamiltonian Path: V-A-B-D-E-
C-F-A’- V”.
 Conversely, if G” contains Hamiltonian Path then we
can convert it to Hamiltonian Cycle by removing end
points (V & V”) and mapping A to A’.
 Thus, G contains Hamiltonian Cycle iff G” contains
Hamiltonian Path which concludes that Hamiltonian
Path is NP COMPLETE.

13. THANK
YOU