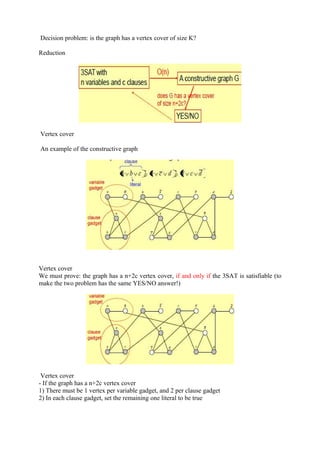
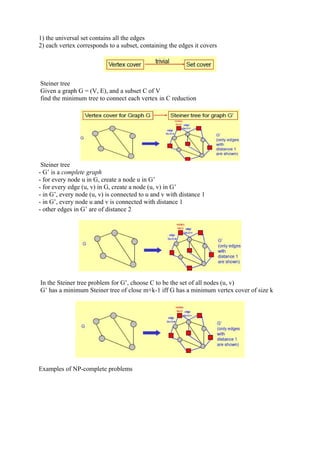
This document discusses NP-hard and NP-complete problems. It begins by defining the classes P, NP, NP-hard, and NP-complete. It then provides examples of NP-hard problems like the traveling salesperson problem, satisfiability problem, and chromatic number problem. It explains that to show a problem is NP-hard, one shows it is at least as hard as another known NP-hard problem. The document concludes by discussing how restricting NP-hard problems can result in problems that are solvable in polynomial time.