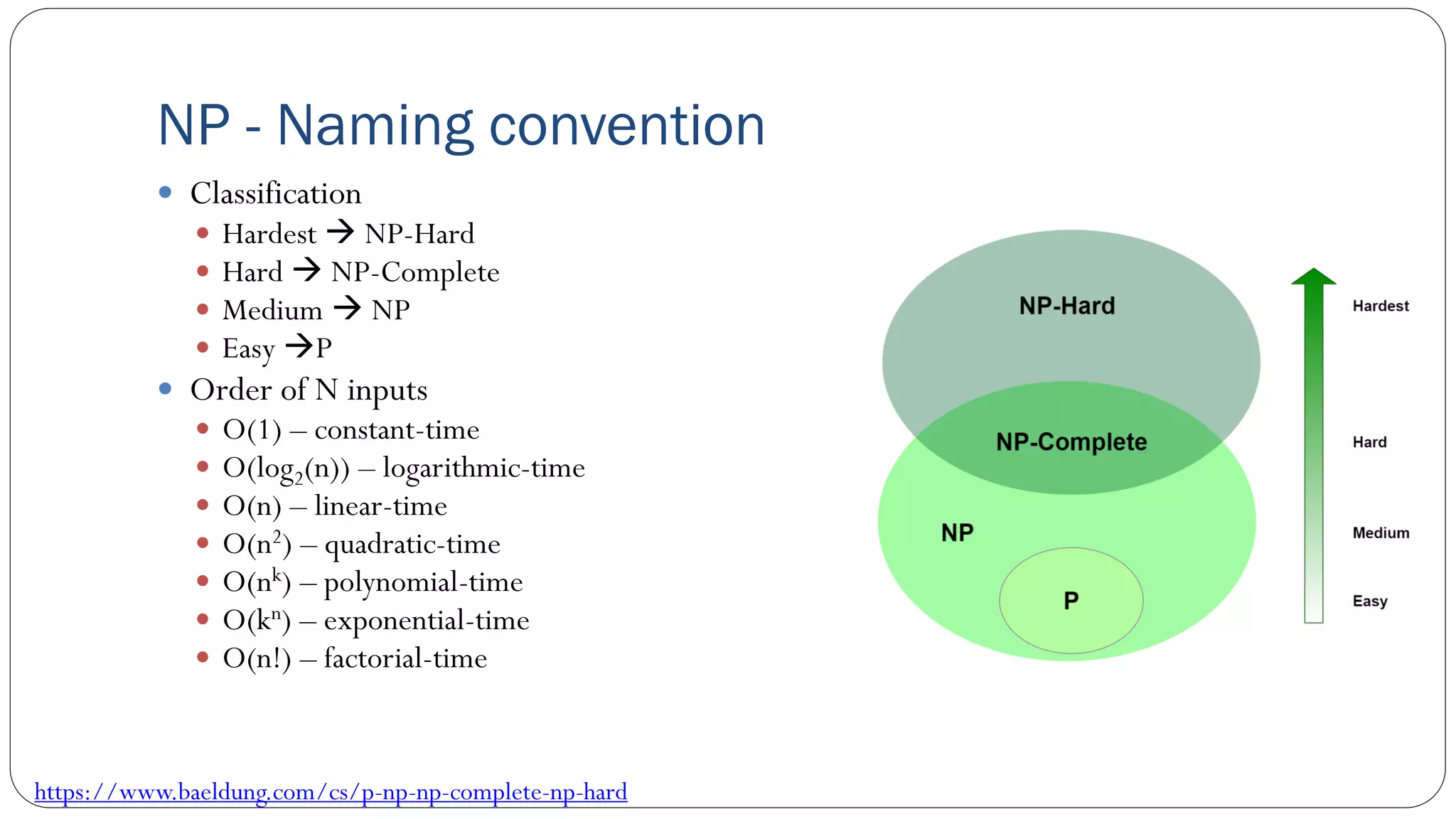
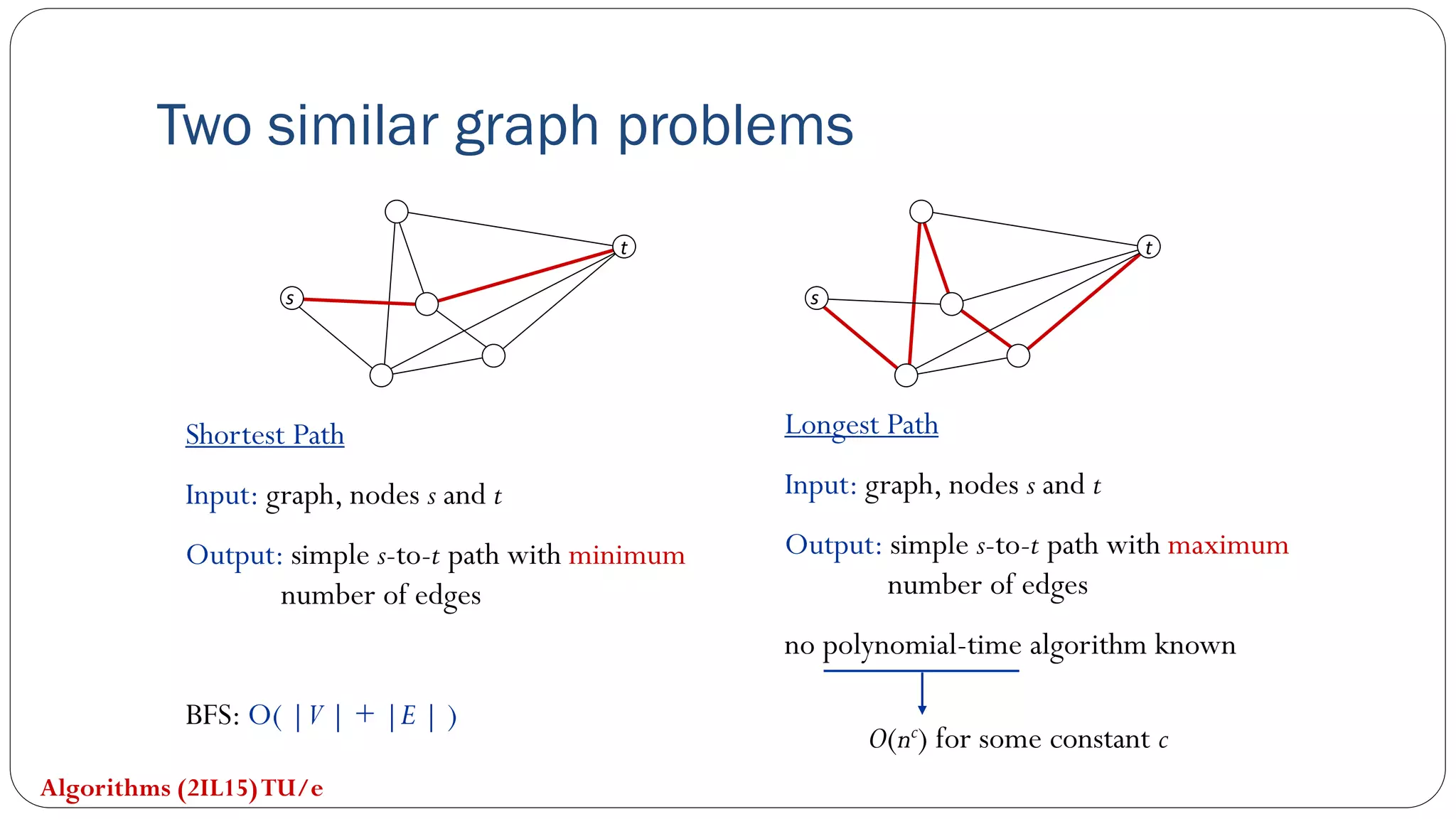
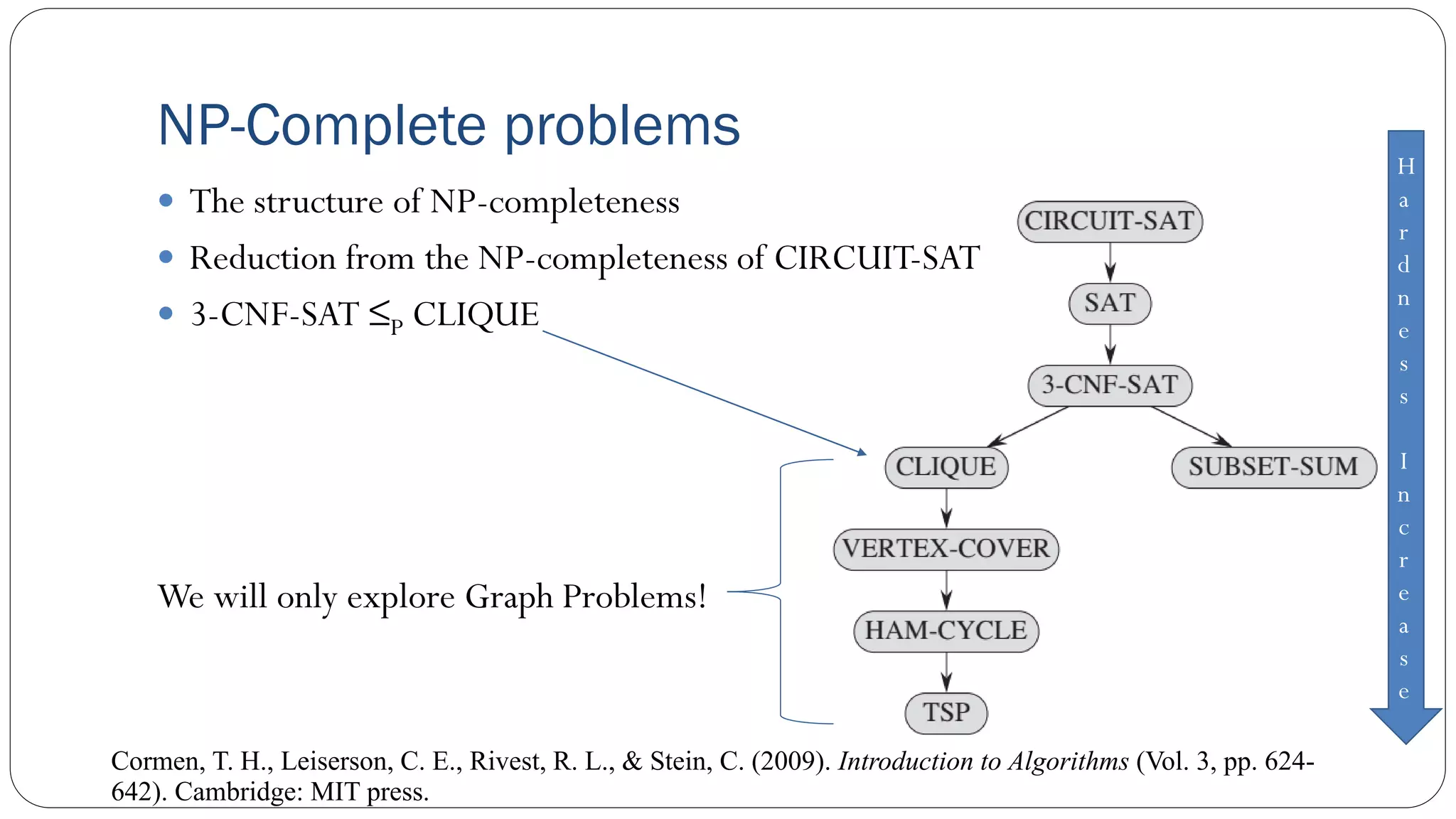
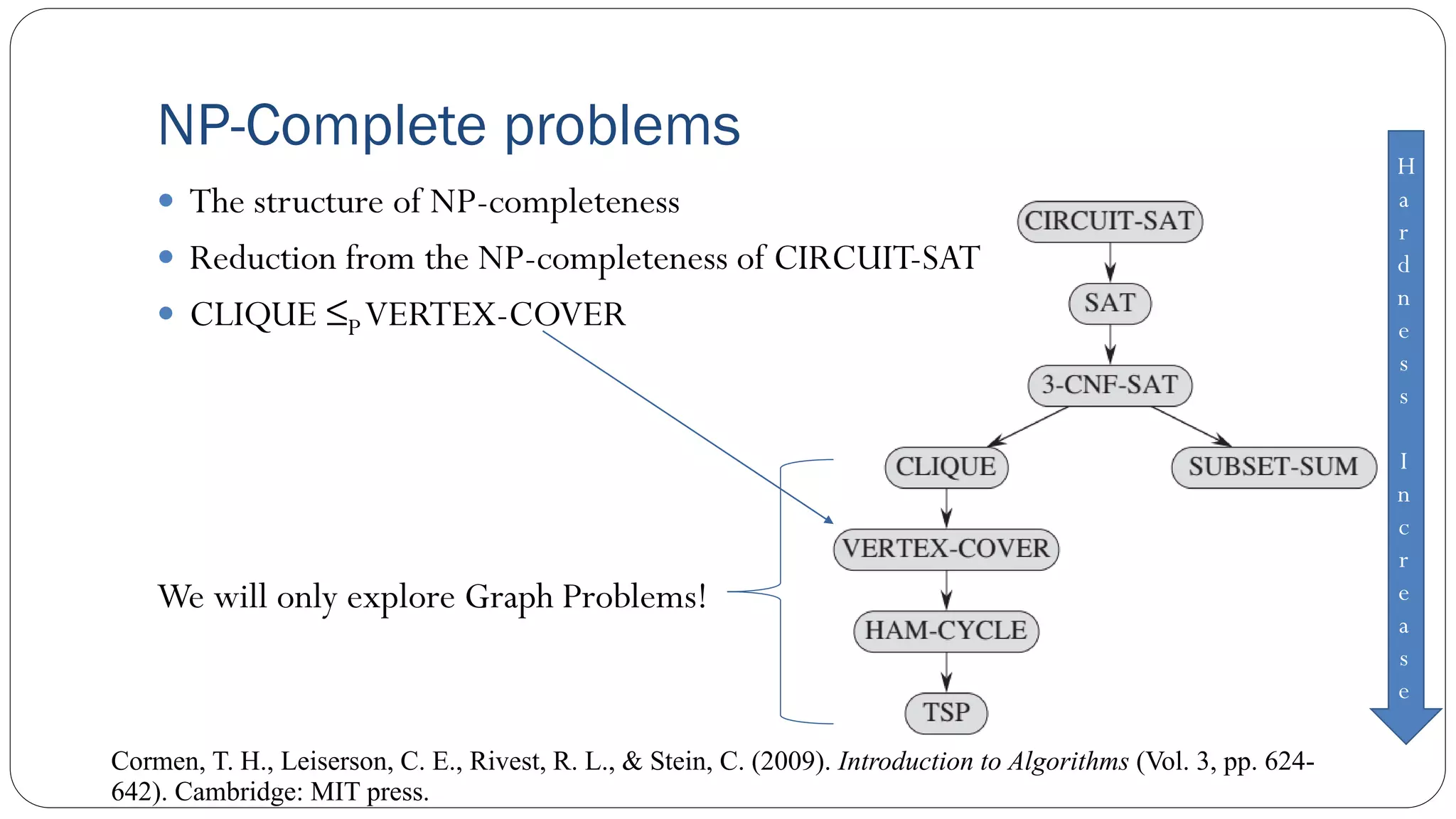
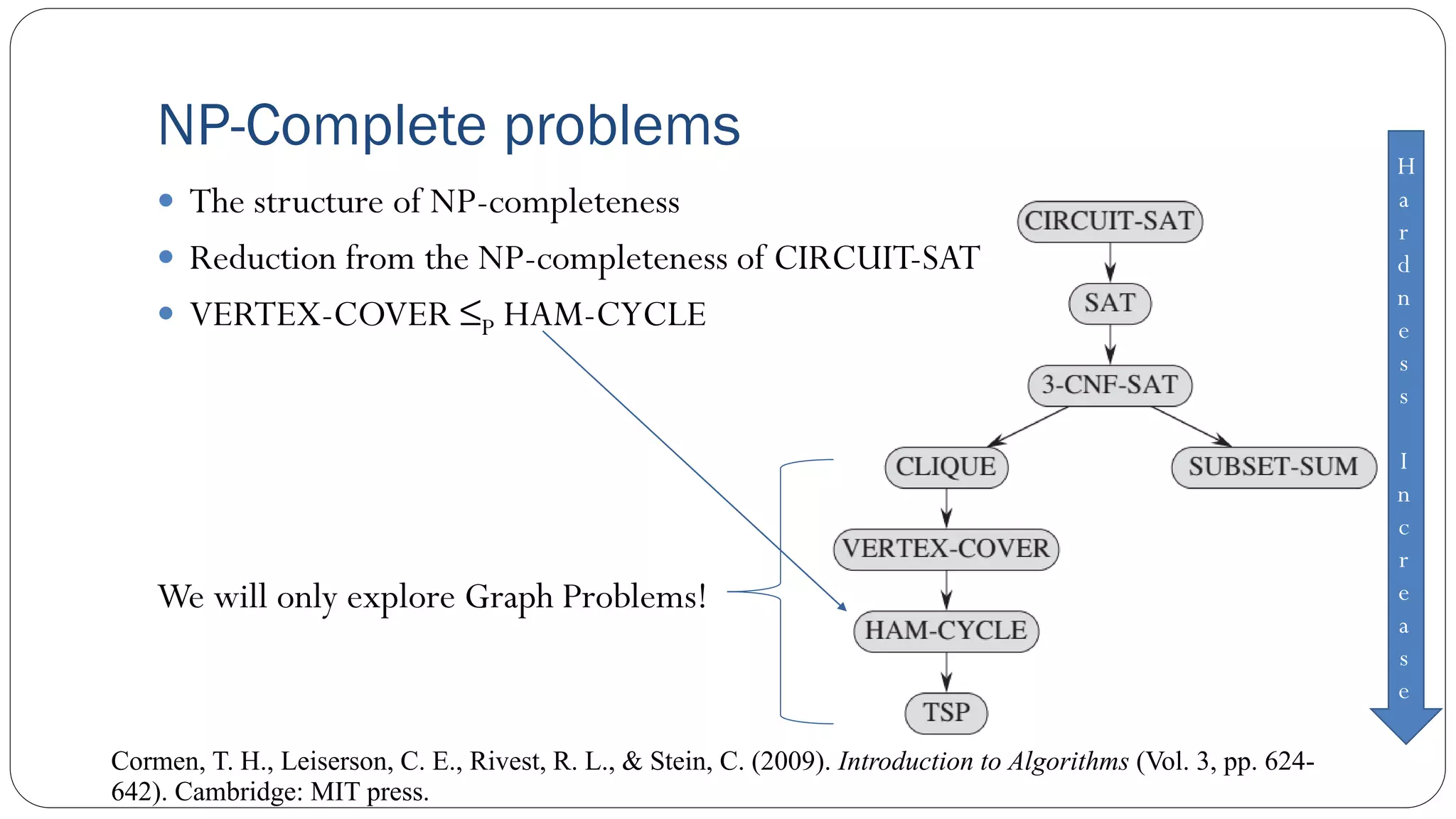
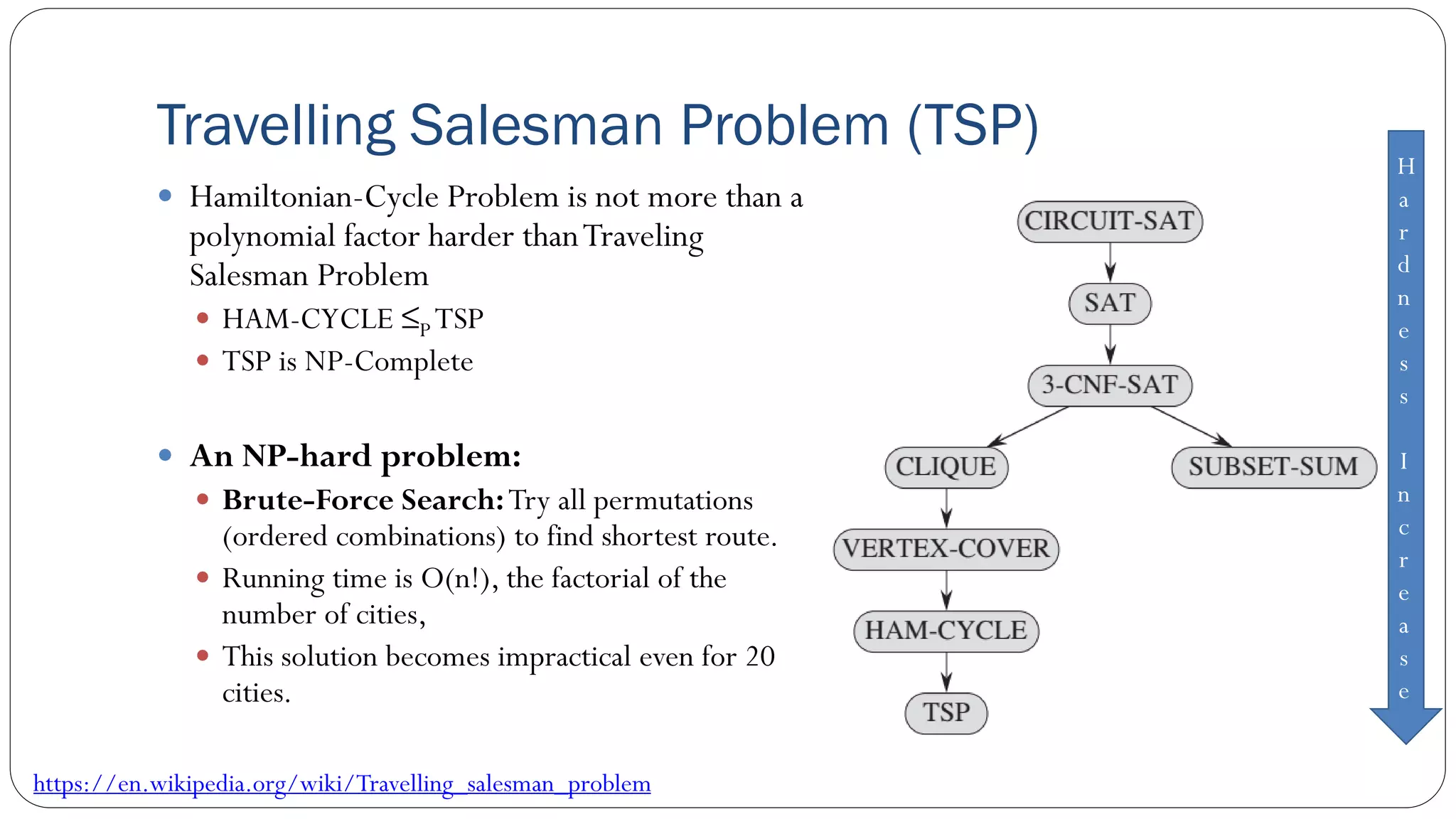
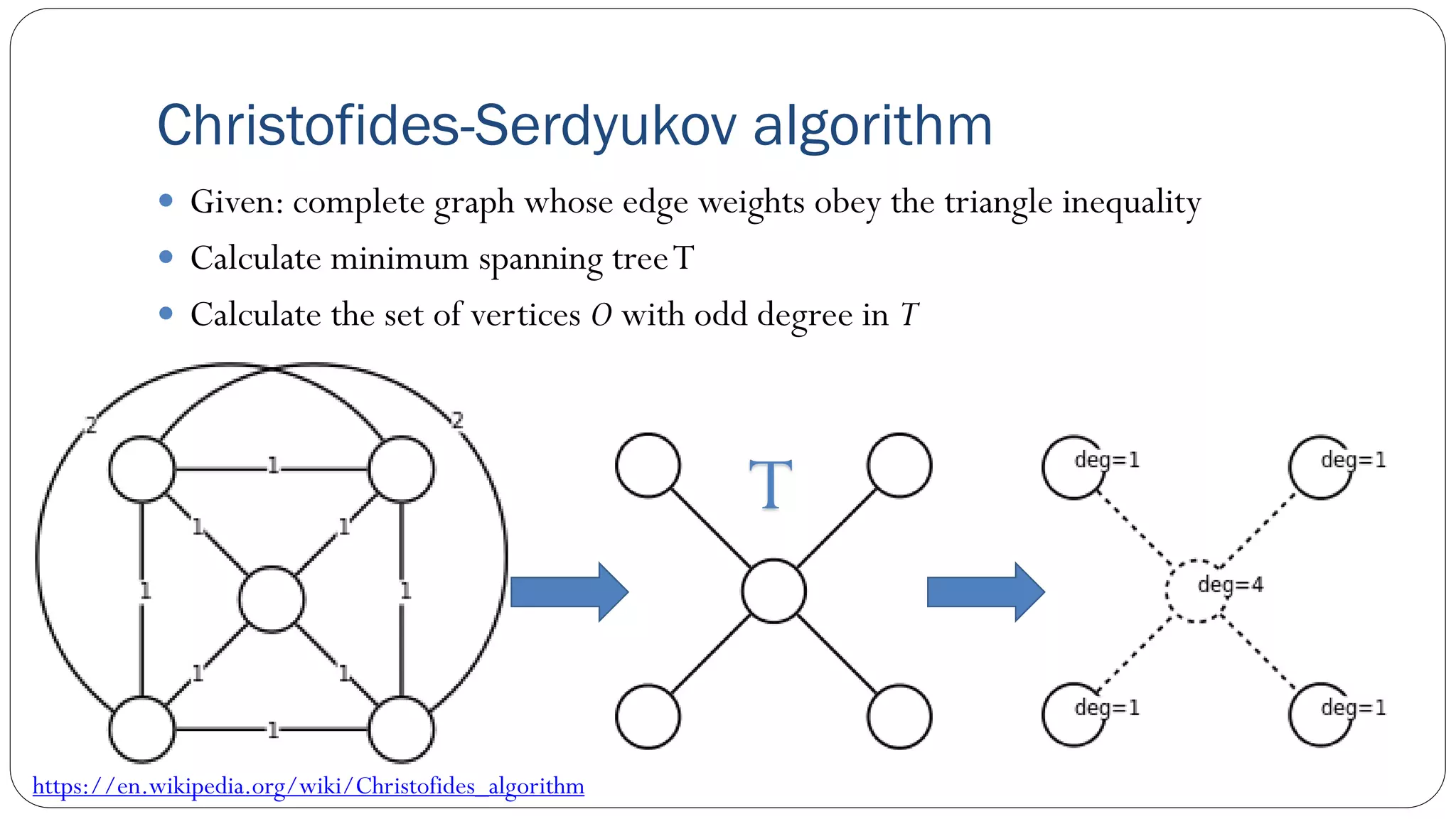
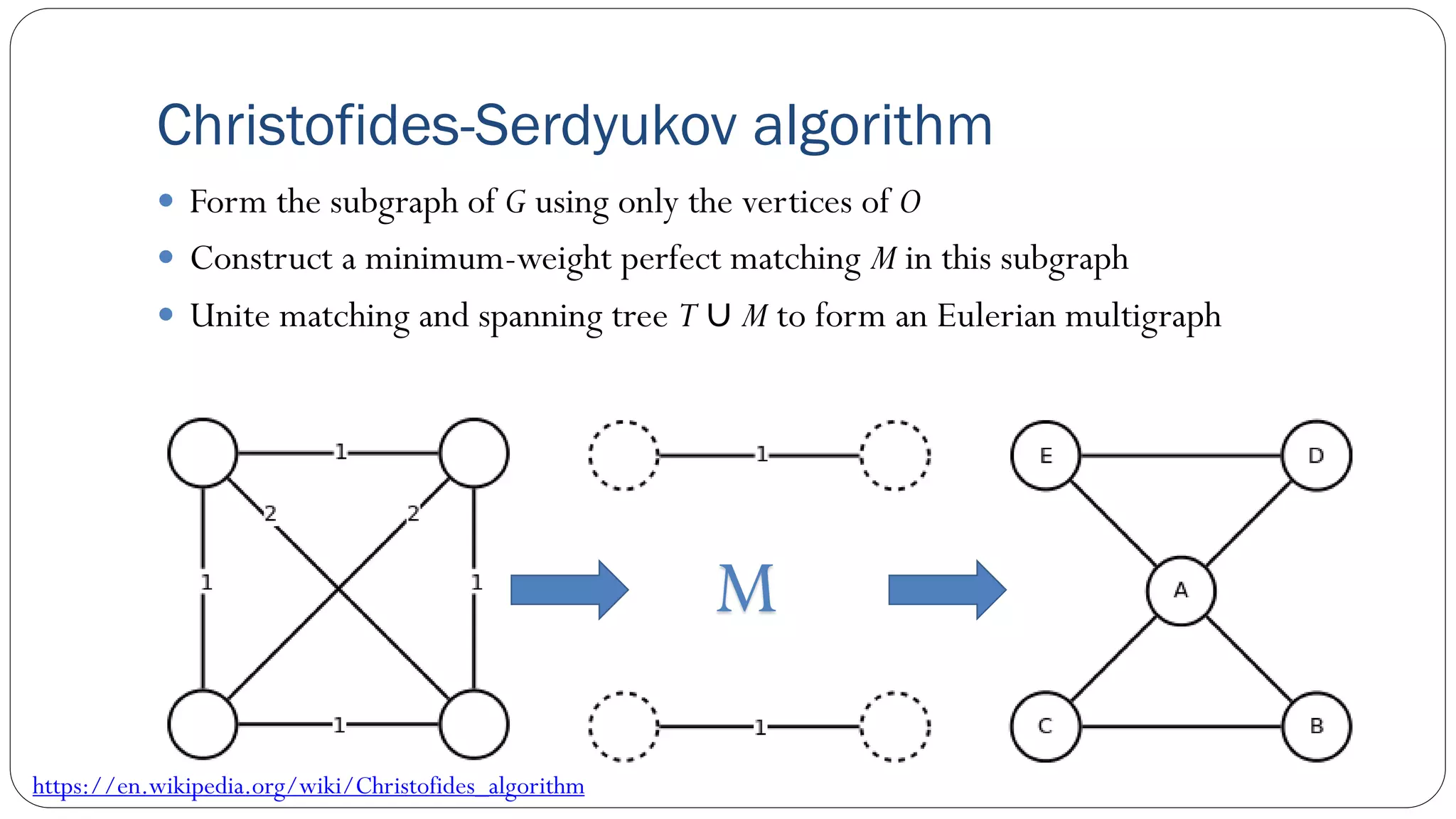
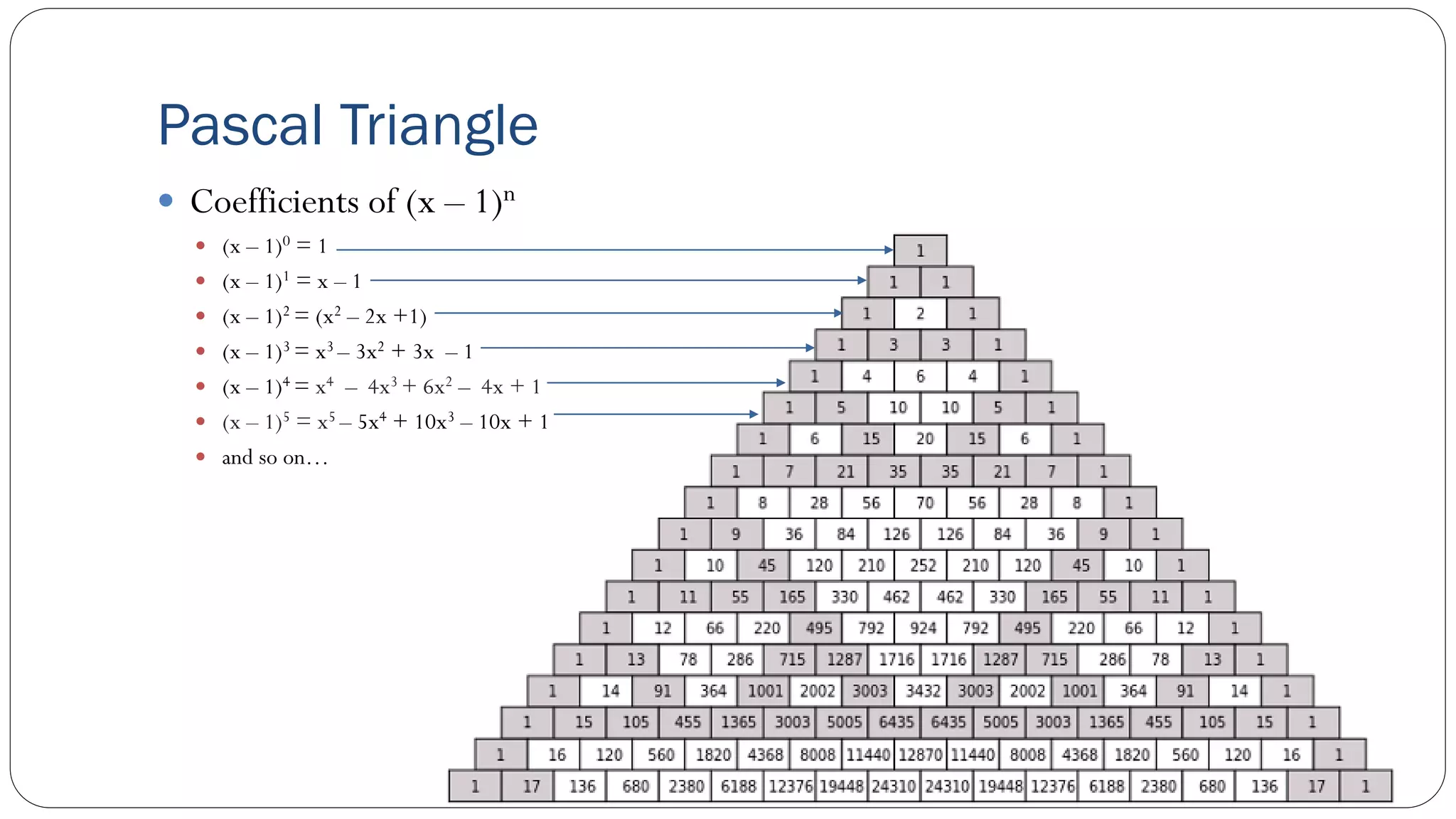
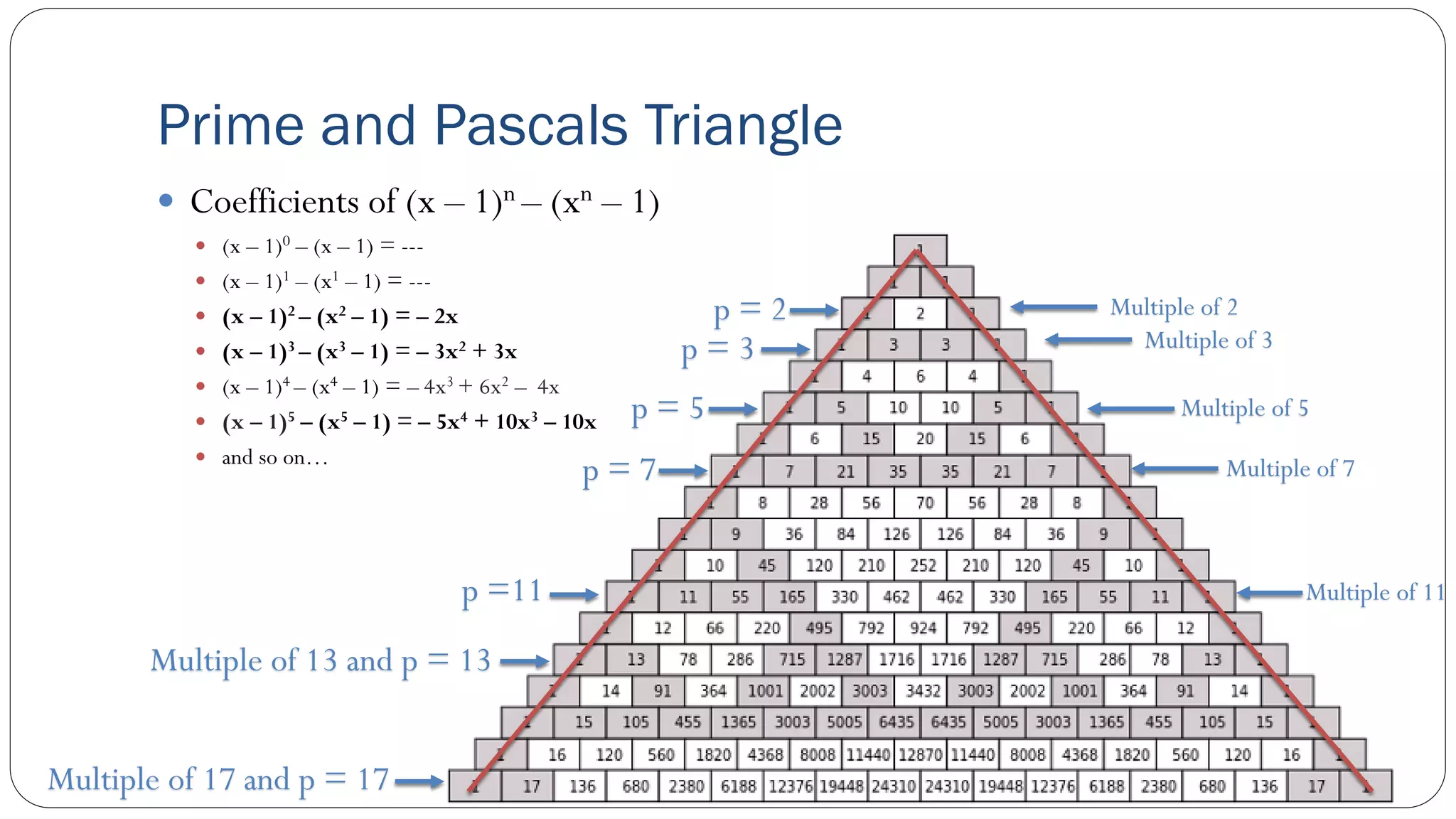
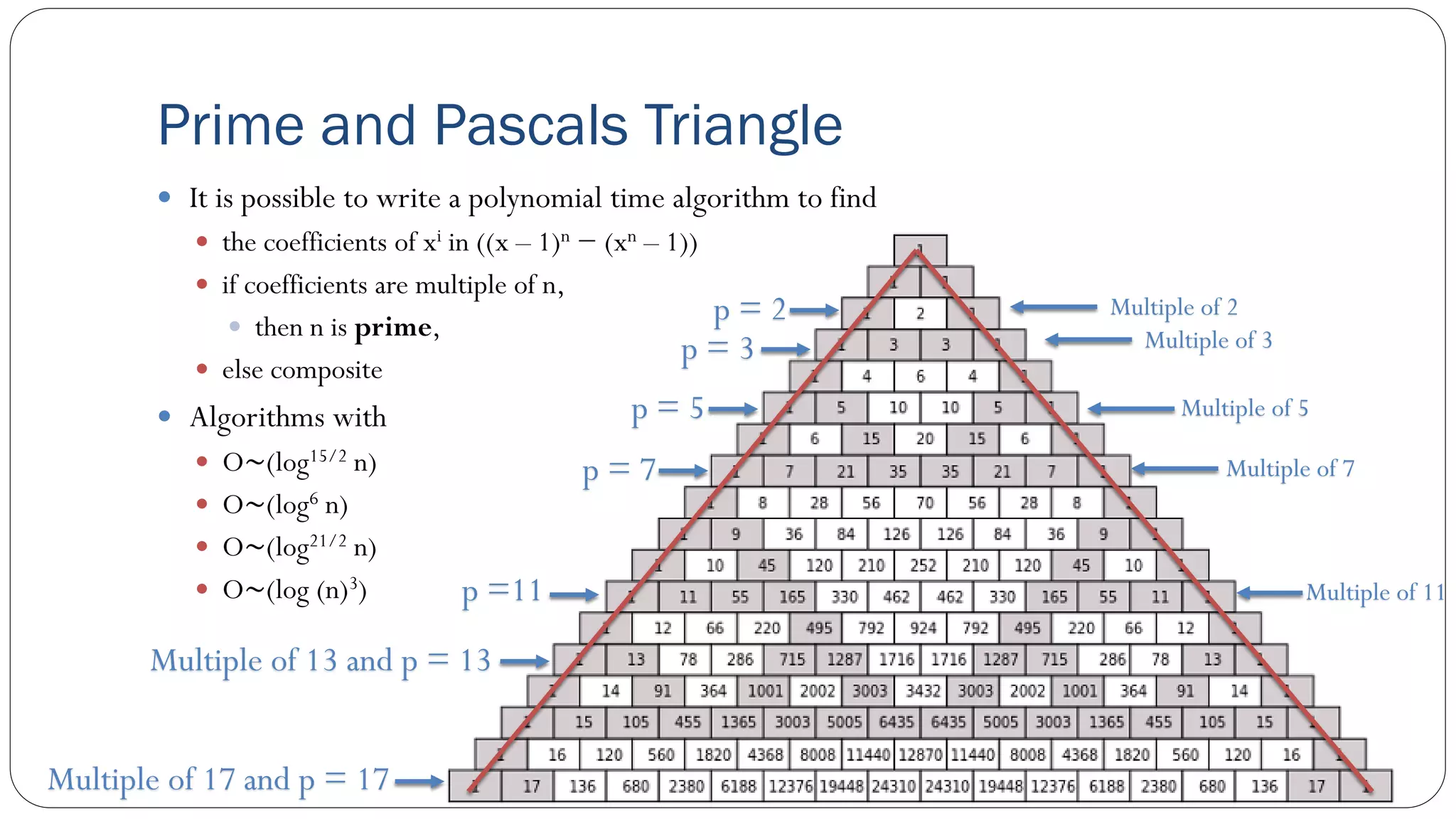
The document covers concepts in computational complexity theory, including classifications of problems such as P, NP, NP-complete, and NP-hard. It explains deterministic vs non-deterministic algorithms, the significance of polynomial-time problems, and reductions in algorithms. Various examples and definitions illustrate the relationship between these complexity classes and highlight the ongoing debate regarding whether P equals NP.