The document discusses Chomsky's hierarchy of formal languages and describes the four types of grammars: 1) Type-3 or regular grammars have productions with a single nonterminal on the left-hand side and a single terminal or terminal-nonterminal on the right-hand side. 2) Type-2 or context-free grammars have productions with a nonterminal on the left-hand side and a string of terminals and nonterminals on the right-hand side. 3) Type-1 or context-sensitive grammars have productions where the left-hand and right-hand sides are strings of terminals and nonterminals, but the right-hand side must be non-empty. 4) Type-

1. Theory of Computation
By Prafull Misra
Roll no. 16013570033

2. Chomsky’s Classification

3. Intro
According to Noam Chomosky, there are four types of grammars −
Type 0 (Unrestricted Grammar)
Type 1 (Context Sensitve Grammar)
Type 2 (Context Free Grammar)
Type 3 (Regular Grammar)
Scope of each type of Grammar

4. Type 3 Grammar (Regular Grammar)
Type-3 grammars must have a single non-terminal on the left-hand side and a right-hand side
consisting of a single terminal or single terminal followed by a single non-terminal.
The productions must be in the form X → a or X → aY
where X, Y ∈ N (Non terminal)
and a ∈ T (Terminal)
The rule S → ε is allowed if S does not appear on the right side of any rule.

5. Type 2 Grammar (Context Free Grammar)
The productions must be in the form A → γ
where A ∈ N (Non terminal)
and γ ∈ (T ∪ N)* (String of terminals and non-terminals).
These languages generated by these grammars are be recognized by a non-deterministic
pushdown automaton.

6. Type 1 Grammar (Context Sensitive Grammar)
The productions must be in the form
α A β → α γ β , where A ∈ N (Non-terminal)
and α, β, γ ∈ (T ∪ N)* (Strings of terminals and non-terminals)
The strings α and β may be empty, but γ must be non-empty.
The rule S → ε is allowed if S does not appear on the right side of any rule.

7. Type 0 Grammar (Unrestricted Grammar)
The productions have no restrictions. They are any phase structure grammar including all formal
grammars.
They generate the languages that are recognized by a Turing machine.
The productions can be in the form of α → β where α is a string of terminals and nonterminals
with at least one non-terminal and α cannot be null. β is a string of terminals and non-terminals.

8. Non-Deterministic Finite Automata with
epsilon moves

9. Introduction to epsilon-NFAs
We extend the class of NFAs by allowing instantaneous (ε) transitions:
1. The automaton may be allowed to change its state without reading the input symbol.
2. In diagrams, such transitions are depicted by labeling the appropriate arcs with ε.
3. Note that this does not mean that ε has become an input symbol. On the contrary, we assume
that the symbol ε does not belong to any alphabet.
4.ε -NFAs add a convenient feature but (in a sense) they bring us nothing new: they do not extend
the class of languages that can be represented. Both NFAs and ε-NFAs recognize exactly the
same languages.

10. Definition of Epsilon-NFA
A ε-NFA is a quintuple A=(Q,Σ,δ,q0,F)
Where,
– Q is a set of states – Σ is the alphabet of input symbols
– q0∈Q is the initial state – F ⊆ Q is the set of final states
– δ: Q ×(Σ ∪ ε) → P(Q) is the transition function
// when we do move from Epsilon-NFA to NFA,
Changes will occur at Final State F and δ values

11. Epsilon-Closure
The ε-closure of the state q is the set that contains q, together with all states that can be reached
starting at q by following only ε-transitions. Example:
Epsilon Closure
q0
q1
q2
q0 q1 q2
q1 q2
q2
q0 q1
q
2ε ε
a b c

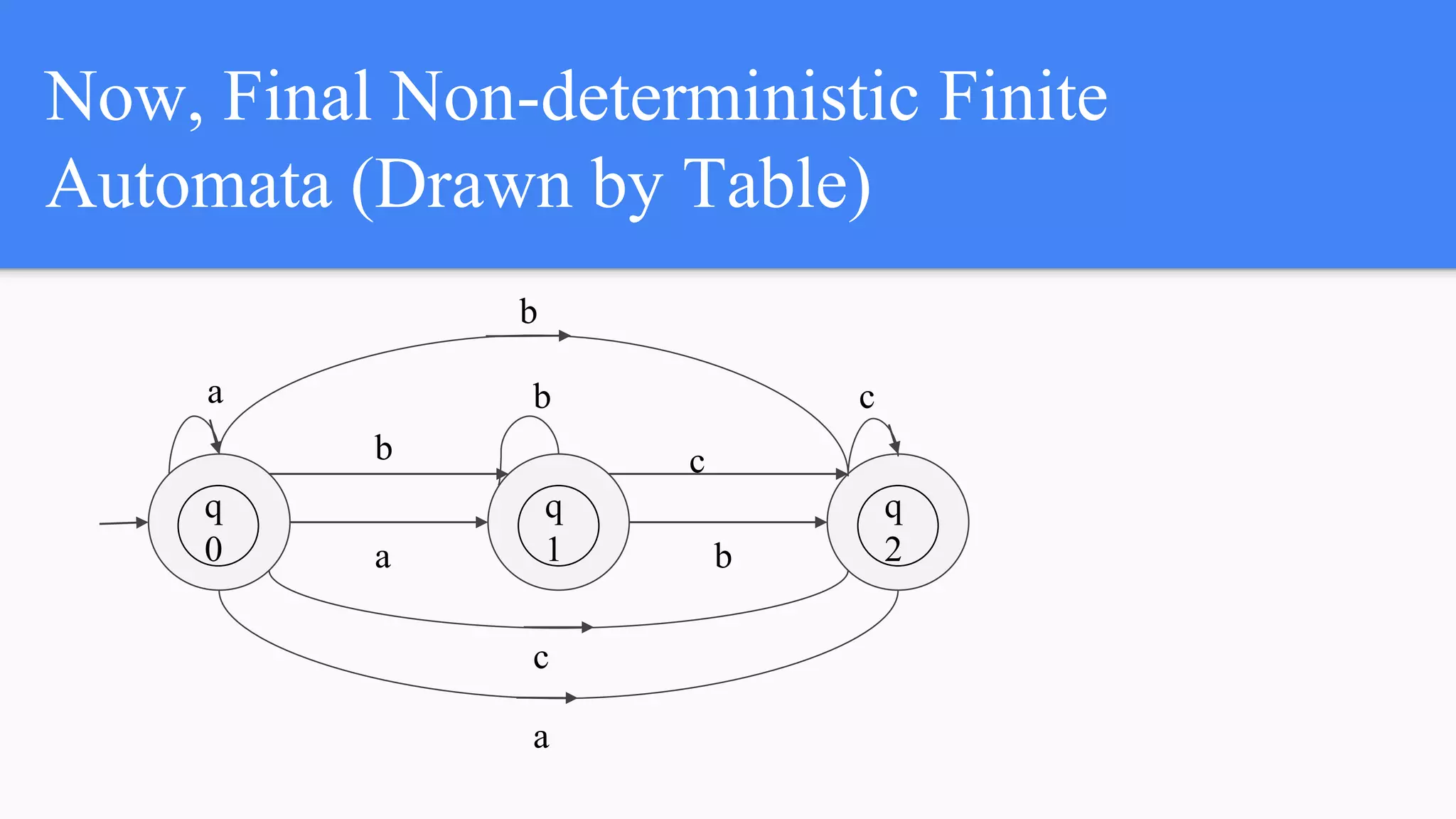
12. Let’s find NFA from given ε-NFA
a b c
q0
q1
q2
q0,q1,q2 q1,q2 q2
Here, for Non-deterministic finite automata
points to be noted,
-Final State will be every state through
which we can lead to final state of Epsilon
NFA via using, ε value.
-Calculation of δ' (qi,x)=ε-cl[δ(ε-cl(qi),Σ)]
Here, ε-cl=to find ε-closure
Ф q1,q2 q2
Ф Ф q2

13. Now, Final Non-deterministic Finite
Automata (Drawn by Table)
q
0
q
1
q
2
a b c
a
a
b
b
c
b
c

14. Multi-tape Turing Machine

15. Introduction
Multi-tape Turing Machines have multiple tapes where each tape is accessed with a separate
head. Each head can move independently of the other heads. Initially the input is on tape 1 and
others are blank. At first, the first tape is occupied by the input and the other tapes are kept blank.
Next, the machine reads consecutive symbols under its heads and the Turing Machine prints a
symbol on each tape and moves its heads.Every Multi-tape Turing machine has an equivalent
single-tape Turing machine.

16. Definition of Multitape Turing Machine
A Multi-tape Turing machine can be formally described as a 6-tuple (Q, X, B, δ, q0, F) where −
-Q is a finite set of states -X is the tape alphabet -q0 is the initial state
-B is the blank symbol -δ is a relation on states and symbols where
δ: Q × Xk → Q × (X × {Left_shift, Right_shift, No_shift })k
,where there is k number of tapes -F is the set of final states

17. Block Diagram of Multitape Turing Machine
-----∞
----- ∞
----- ∞
Transition Logic
(Control Unit)
∞-----
∞-----
∞-----

18. Theory of Computation – Basic Definitions

19. Alphabets:
Theory of computation is entirely based on symbols. These symbols are generally letters and
digits.
Alphabets are defined as a finite set of symbols. Represented by ∑.
Examples:
∑ = {0, 1} is an alphabet of binary digits
∑ = {A, B, C, …., Z} is an alphabet.

20. Strings:
A string is a finite sequence of symbols selected from some alphabet. It is generally denoted as
w.For example for alphabet ∑ = {0, 1} w = 010101 is a string.
Length of a string is denoted as |w| and is defined as the number of positions for the symbol in the
string. For the above example length is 6.
The empty string is the string with zero occurrence of symbols. This string is represented as є or
λ.

21. Languages:
A language is a set of string all of which are chosen from some ∑*, where ∑ is a particular
alphabet. This means that language L is subset of ∑*.
Concatenation of Languages :
If L1 and L2 are two languages then their concatenation can be defined as :
L = L1 . L2 where L = {w: w = xy where x є L1, y є L2}
It means that all the strings in the language L are concatenation of stings of language L1 and L2

22. Kleen Closure and Positive Closure:
Kleene closure ( Kleene star or Kleene operator):
It is an operator in Theory of Computation, which gives the infinite set of all possible lengths of
strings including zero length string over some input ∑ .
Example − If ∑ = {0, 1}, ∑* = {zero length string, 0, 1, 01, 10,…}
Positive Closure:
We have Kleen plus which is just a modification(∑* − { zero length string }) over Kleen start.
Example − If ∑ = {0, 1}, ∑+ = { 0, 1, 01, 10,…}

23. Automata:
A algorithm or program that automatically recognizes if a particular string belongs to the
language or not, by checking the grammar of the string. An automata is an abstract computing
device (or machine). There are different varities of such abstract machines (also called models of
computation) which can be defined mathematically.
This automata consists of
-states (represented in the figure by circles), - and transitions (represented by arrows).

24. Thanks!