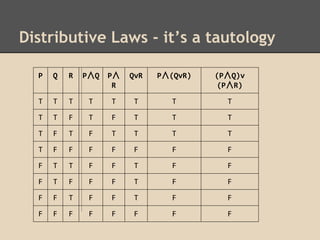
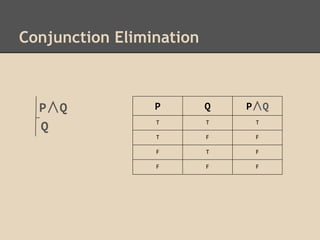
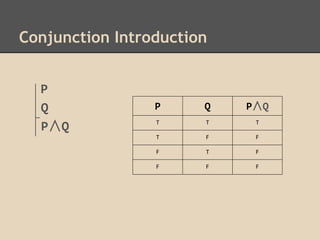
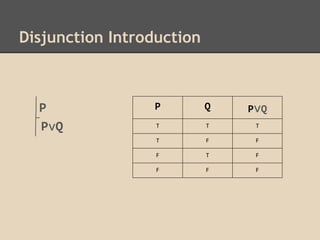
This document discusses different proof techniques in Boolean logic, including: - Distributive laws for conjunction over disjunction. - Converting expressions to disjunctive normal form using distribution. - Inference steps like conjunction elimination, conjunction introduction, and disjunction introduction. - Proof by cases, where you prove each disjunct yields the conclusion. - Proof by contradiction, where you assume the negation and deduce a contradiction. - Examples are given for each technique.

1. Truth, Deduction,
Computation
Lecture 6
Boolean Logic and Informal Proofs
Vlad Patryshev
SCU
2013

2. Distributive Laws
● P∧(QvR) ⇔ (P∧Q) v (P∧R)
● P∧(QvR) ⇔ (PvQ) ∧ (PvR)

3. Distributive Laws - it’s a tautology
P
Q
R
P∧Q
P∧
R
QvR
P∧(QvR)
(P∧Q)v
(P∧R)
T
T
T
T
T
T
T
T
T
T
F
T
F
T
T
T
T
F
T
F
T
T
T
T
T
F
F
F
F
F
F
F
F
T
T
F
F
T
F
F
F
T
F
F
F
T
F
F
F
F
T
F
F
T
F
F
F
F
F
F
F
F
F
F

4. Disjunctive Normal Form (example)
(A∨B)∧(C∨D) ⇔ ((A∨B)∧C)∨((A∨B)∧D)
⇔ (A∧C)∨(B∧C)∨((A∨B)
∧D)
⇔ (A∧C)∨(B∧C)∨(A∧D)∨
(B∧D)

5. Disjunctive Normal Form
<dnf> ::= <conjunction>
<dnf> ::= <dnf> v <conjunction>
<conjunction> ::= <literal>
<conjunction> ::= <conjunction>∧<literal>
<literal> ::= <atomic formula>
<literal> ::= ¬<atomic formula>
E.g. (¬A∧B∧C)v(A∧¬C)v(¬B∧¬C)

6. Disjunctive Normal Form (in code)
class DNF(cc: Conjunction*)
class Conjunction(ll: Literal*)
trait Literal
class Negative(f: Atomic) extends Literal
class Positive(f: Atomic) extends Literal
trait Name
class Atomic(predicate:Name, params:Term*)
trait Term
class Fun(function: Name, params: Term*)
extends Term
class Entity(name:Name) extends Term

7. (Chapter 5)
Boolean Logic: Ways to Prove
Problems with truth tables
● exponential growth
● not enough valid combinations
Have to find shortcuts, “inference steps”

8. Inference Steps - Informally
Important (informal) rules of thumb
● If everybody agree that P yields Q, it does
● If we know that Q is a logical truth, reuse it

9. Inference Steps - Formally
● Conjunction Elimination
● Conjunction Introduction
● Disjunction Introduction

10. Conjunction Elimination
P∧Q
Q
P
Q
P∧Q
T
T
T
T
F
F
F
T
F
F
F
F

11. Conjunction Introduction
P
Q
P∧Q
P
Q
P∧Q
T
T
T
T
F
F
F
T
F
F
F
F

12. Disjunction Introduction
P
PvQ
P
Q
PvQ
T
T
T
T
F
F
F
T
F
F
F
F

13. Proof by Cases
To prove S1vS2..Sn yields Q,
Prove that S1 yields Q, S2
yields Q… Sn yields Q.

14. Proof by Cases - Example
Ex. 5.4
(Home(max)∧Happy(carl)) v (Home(claire)∧Happy(scruffy))
Happy(carl) v Happy(scruffy)

15. Proof by Cases - Another Example
Can a rational a be equal to bc where b and c are irrational?
1.
2.
sqrt(2) is irrational (proof?)
Either…
a. q = sqrt(2)sqrt(2) is rational (QED), or…
b. q is irrational, and qsqrt(2)=sqrt(2)sqrt(2)*sqrt(2)=sqrt(2)2=2

16. Proof by Contradiction
Reductio ad Absurdum
To prove ¬S, assume S, and
deduce ⊥.
(⊥ is called “contradiction symbol”)

17. Proof by Contradiction - Example
Is sqrt(2) irrational?
1.
2.
3.
4.
5.
Assume it is, sqrt(2)=p/q
Where p and q are mutually prime (have no common divisors)
Then p2=2*q2
Then both p and q must be even.
⊥
We used our (tautological) knowledge that
A ∧ ¬A
FALSE

18. Proof by Contradiction - Example

19. Inconsistent Premises (are the best)
● never sound
● always valid

20. That’s it for today