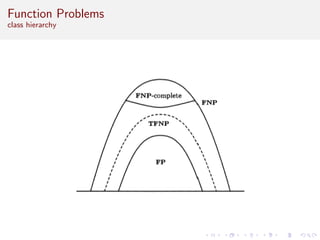
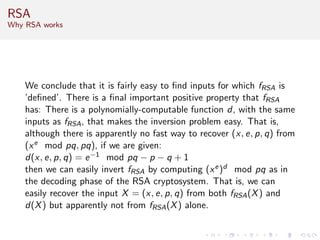
This document discusses algorithms and complexity in cryptography. It begins by defining function problems in computational complexity theory as computational problems where the expected output is more complex than a simple yes or no answer. It then discusses one-way functions, which are easy to compute but believed to be hard to invert. The document provides examples of one-way functions based on integer multiplication, discrete logarithms, and the RSA cryptosystem. It argues that the existence of one-way functions separates the complexity classes P and UP, and that cryptography relies on the assumption that stronger versions of one-way functions exist.

1. Algorithms and Complexity
Cryptography Theory
Alex Prut
Universit`a degli studi di Udine
January 31, 2017

2. 1 Introduction
The Problem
2 Function Problems
Definition
3 Protocols

3. Introduction
The Problem
Definition (informal, alice and bob problem)
Two parties (Alice & Bob) wish to communicate in the presence of
malevolent eavesdroppers. That is, Alice wants to send a message
to Bob, over a channel monitored by an adversary (Eve), and
wishes the messages to be knows only to her and Bob. Alice &
Bob agree on two algorithms E (encoding) and D (decoding),
known to general public. Alice runs y = E(e, x), who wish to send
message x ∈ Σ∗(Σ = {0, 1}), Bob receives y and computes
x = D(d, y). Privacy is assured in terms of two strings e, d ∈ Σ∗
known only to Alice & Bob.

4. Perfect solution
One-time pad
Definition (One-time pad)
Let both d, e be the string e of length |x|.
Let E(e, x) and D(e, y) be the exclusive or.
E(e, x) = e ⊕ x = y and D(e, y) = e ⊕ y = x that is the ith bit is
one ⇐⇒ exactly one of ei , yi = 1).
Since ((x ⊕ e) ⊕ e) = x we have that D(d, E(e, x)) = x
Cons:
the key must be as long as the message (i.e. e = |x|)
Alice & Bob need to agree and exchange the key e

5. Perfect solution
Public-Key Cryptosystem
Definition (Public-Key Cryptosystem (informal))
Suppose that only d is secret and private to Bob, while e is known
to Alice and general public. Bob generates the (e, d) pair and
announces e openly. Alice can send a message x to Bob by
computing and trasmitting E(e, x) where D(d, E(e, x)) = x.
.
The point is that it is computationally infeasible to deduce d
from e, and x from y without knowing d.
Secure key cryptosystem can exists only if P = NP, even that it is
not immediate.
W.Diffie,
M.E.Hellman - IEEE Trans. on Information Theory, 22,
pp. 664, 1976

6. Function Problem
Function Problem
Definition (function problem)
In computational complexity theory, a function problem is a
computational problem where a single output (of a total function)
is expected for every input, but the output is more complex than
that of a decision problem, that is, it isn’t just YES or NO.

7. Function Problems
Relation between decision and function problems
Definition (Relation between decision and function problems, FNP)
Given L ∈ NP. There is a polynomial-time decidable, polynomially
balanced relation RL such that for all strings x:
There is a string y with RL(x, y) ⇐⇒ x ∈ L.
The function problem associated with L, denoted FL is the
following computational problem:
Given x, find a string y such that RL(x, y) if such a string exists; if
no return ’no’

8. Function Problems
more definitions/theorems
Definition (Reduction)
A function problem A reduces to function problem B if the
following holds:
There are string functions R and S, both computable in logarithmic
space, such that for any string x and z the following holds:
1 If x is an instace of A then R(x) is an istance of B
2 If z is the correct output of R(x) then S(z) is a correct
output of x
Definition (F-Complete)
A function problem A is complete for a class FC of function
problems if it is in FC and all problems in that class reduce to A.

9. Function Problems
more definitions/theorems
Definition (FSAT)
FSAT is FNP-Complete.
Theorem
FP = FNP ⇐⇒ P = NP.
Definition (TFNP)
A problem R is FNP total if for every string x there is at least one
string y such that R(x, y). The subclass of FNP containing all
total function problems is denoted TFNP.
N.Megiddo, C.H.Papadimitriou - Theor. Comp. Sci., 81,
1991

10. Function Problems
class hierarchy

11. Function Problems
One-way function
Definition (One-way function)
Let f : Σ∗ → Σ∗ be a function from strings to strings. We say that
f is one-way function if the following holds:
1 f is one-to-one and for all x ∈ Σ∗, |x|1/k ≤ |f (x)| ≤ |x|k for
some k > 0,
f (x) is at most polynomially longer or shorter than x.
2 f is in FP, can be computed in polynomial time
3 the inverse f −1 is not in FP, i.e. there is no polynomial-time
algorithm which given y either computes an x such that
f (x) = y or returns ’no’
Even if P = NP there is no guarantee that one-way functions exist.

12. One-way function
Integer multiplication with primes
Definition (Integer multiplication with primes)
fMULT (p, q) =
(p, q) if p, q not prime numbers
p · q otherwise
(1)
Many people suspect is indeed a one-way function.
We know of no polynomial algorithm which inverts f (i.e. factor
products of large primes)

13. One-way function
Discrete logarithm problem
Definition (Exponentiation modulo a prime)
Given fEXP, p a prime number, a primitive root r modulo p and an
integer x < p:
fEXP(p, r, x) = (p, rx mod p)
Inverting fEXP is another well-known hard computational problem
in number theory called discrete logarithm problem, for which no
polynomial-time algorithm is known.

14. RSA
RSA function
Definition (RSA function)
As the basis of a public-key cryptosystem a clever combination of
fMULT and fEXP can be exploited. Let p, q be two prime numbers,
consider their product p · q. The number of bits of pq is
n = logpq . Suppose that e is a number that is relatively prime to
φ(pq) = pq(1 − 1/p)(1 − 1/q) = pq − p − q + 1 (Euler function).
The RSA function:
fRSA(x, e, p, q) = (xe mod pq, pq, e)
No polynomial algorithm for inverting the RSA function has been
announced.
R.L.Rivest, A.Shamir, L.Adleman - C.ACM, 22, pp. 120,
1978

15. RSA
RSA public-key cryptosystem
RSA function can be the basis of a public-key cryptosystem. Bob
knows p, q and announces their product pq as well as e (i.e. an
integer prime to φ(pq)). The public key of Bob is (pq, e).
Alice uses the public key to encrypt message x (an n bits integer)
as follows:
y = xe mod pq
Bob knows besides Alice an integer d (i.e. a residue modulo pq)
such that e · d = 1 + kφ(pq) for some integer k (d can be found
by the Euclid’s algorithm).
In order to decrypt y Bob simply computes:
yd = xe·d = x1+kφ(pq) = x mod pq
simply because xφ(pq) = 1 mod pq (Fermat’s theorem).

16. Cryptography and Complexity
UP
Definition (Unambiguous nondeterministic Turing machine)
Call a nondeterministic Turing machine unambiguous if it has the
following property:
1 For any input x there is at most one accepting computation.
UP is the class of languages accepted by unambiguous
polynomial-time bounded nondeterministic Turing machines.
It is obvious that P ⊆ UP ⊆ NP
L.G.Valiant - Inf. Proc. Letters, 5, pp.20, 1976

17. Cryptography and Complexity
UP
Theorem
P = UP ⇐⇒ there are no one-way functions
Proof.
⇐
Suppose that there exist a one-way function f . We consider
Lf = {(x, y) : there is z s.t. f (z) = y and z ≤ x}. In writing z ≤ x
we assume that all strings in {0, 1}∗ are ordered, first by length
and strings of the same length n are ordered lexicographically. We
claim that Lf ∈ UP − P. It is easy to see that there is an
unambiguous machine U that accepts Lf on input (x, y),
nondeterministically guesses a string z of length at most |y|k and
tests whether y = f (z). If the answer is ’yes’ it checks whether
z ≤ x and if so accepts it. Hence Lf ∈ UP. continue...

18. Cryptography and Complexity
UP
Proof.
We have to show now that Lf /∈ P. Suppose there is a
polynomial-time algorithm for Lf . Then we can invert the one-way
function f by binary search: Given y we ask whether
(1|y|k
, y) ∈ Lf . If the answer is ’no’ this means that there is no x
s.t. f (x) = y if there were such an x it would have to be
lexicographically smaller than 1|y|k
since |y| ≥ |x|1/k. If the answer
is ’yes’ then we ask whether (1|y|k −1) ∈ Lf , and then (1|y|k −2) ∈ Lf
and so on until for some query (1l−1, y) ∈ Lf we get the answer
’no’ and thus determine the actual length l ≤ |y|k of x. We then
determine one-by-one the bits of x again by asking whether
(01l−1) ∈ Lf and then depending on whether the answer was ’yes’
or ’no’, asking (001l−2) ∈ Lf or (101l−2) ∈ Lf and so on. After a
total of at most 2nk application of the polynomial algorithm for Lf
we have inverted f on y.

19. Cryptography and Complexity
UP
Proof.
⇒
Suppose that there is a language L ∈ UP − P. Let U be the
unambiguous nondeterministic Turing machine accepting L, and let
x be an accepting computation of U on input y; we define
fU(x) = 1y, that is, the input of U for which x is an accepting
computation prefixed by the flag 1. If x does not encode a
computation of U, fU(x) = 0x, the flag now is 0 meaning that the
the argument of fU is not a computation. We claim that fU is
one-way function. It is a well-defined function in FP because y is a
part of the representation of the computation x and can be
essentially read off x. Second, the lengths of argument and result
are polynomially related, as required, because U has polynomially
long computations. continue...

20. Cryptography and Complexity
UP
Proof.
The function is one-to-one, because since the machine is
unambiguous. And if we could invert fU in polynomial time, then
we would be able to decide L in polynomial time as well.
Thus, the correct complexity context for discussing cryptography
and one-way functions is the P
?
= UP question not the P
?
= NP
one.
We fully expect that P = UP.
UP is not known or believed to have complete problems.

21. Function Problems
Stronger one-way function
Definition (Stronger one-way function)
A definition of one-way functions that is closer to what we need in
cryptography would replace requirement:
(iii)—that inverting is worst-case difficult—by a stronger
requirement, that there be no integer k, and no algorithm which,
for large enough n, in time O(nk) successfully computes f −1(y) for
at least 2n/nk strings y of length n.
That is, there is no polynomial-time algorithm that
successfully inverts f on a polynomial fraction of the inputs
of length n.
Levin - Proc. 16th ACM,
Symposium on the Theory of Computing - 1984

22. RSA
Why RSA works
We conclude that it is fairly easy to find inputs for which fRSA is
’defined’. There is a final important positive property that fRSA
has: There is a polynomially-computable function d, with the same
inputs as fRSA, that makes the inversion problem easy. That is,
although there is apparently no fast way to recover (x, e, p, q) from
(xe mod pq, pq), if we are given:
d(x, e, p, q) = e−1 mod pq − p − q + 1
then we can easily invert fRSA by computing (xe)d mod pq as in
the decoding phase of the RSA cryptosystem. That is, we can
easily recover the input X = (x, e, p, q) from both fRSA(X) and
d(X) but apparently not from fRSA(X) alone.

23. Function Problems
Trapdoor functions
Definition (Trapdoor functions)
To summarize the additional properties of the RSA function,
besides (1), (2) and (3) of one-way functions, that we indentified
in this discussion:
4 We can efficiently sample the domain of the one-way function
5 There is a polynomially computable function d of the input
that trivializes the inversion problem.
We call one-way function that has properties (4) and (5) a
trapdoor function
If Factorization /∈ P then fRSA is a trapdoor function.

24. Randomized public-key cryptosystem
RSA problem
There are two very important messages that are always easy to
decode: Suppose that Alice and Bob communicate using the RSA
public-key cryptosystem, and very often Alice needs to send to Bob
a single confidential bit b ∈ {0, 1}. Should Alice encrypt this bit as
an ordinary message, be mod pq?
Obviously not. Since be = b for b ∈ {0, 1}, the encrypted message
would be the same as the original message i.e. not encrypted at
all. Single bits are always easy to decode. There is simple remedy
for the last problem. Alice could generate a random integer
x ≤ pq/2 and then transmit to Bob y = (2x + b)e mod pq. Bob
receives y, and uses this private key to recover 2x + b: b is the last
bit of the decrypted integer.

25. Randomized public-key cryptosystem
RSA problem
The resulting randomized public-key cryptosystem is much slower
than the original RSA, which transmits several hundreds of bits at
once. The point is that it is much more secure: detecting
repetitions, luckily recovering crucial messages, etc. are not
present in the randomized public-key cryptosystem.

26. Protocols
Signature protocol
Definition (Signature problem (informal))
Suppose that Alice wants to send Bob a signed document x. But
what does this mean? Minimally, a signed message SAlice(x) is a
string that contains the information in the original message x, but
is modified in a way that unmistakably identifies the sender.
Public-key cryptosystem provide an elegant solution to the
electronic signature problem.

27. Protocols
Signature
Suppose that both Alice & Bob have public and private keys
eAlice, dAlice, eBob, dBob. We assume they both use the same
encoding, decoding functions. Alice signs x as:
SAlice(x) = (x, D(dAlice, x))
A message decrypted as if it were an encrypted message received
by Alice. Bob upon receipt of SAlice(x) takes the second part and
encodes it using Alice’s public key:
E(eAlice, D(dAlice, x)) = D(dAlice, E(eAlice, x)) = x
The RSA cryptosystem is clearly commutative, since:
D(d, E(e, x)) = (xe)d mod pq = (xd )e mod pq = E(e, D(d, x))

28. Protocols
Mental Poker problem
Definition
Suppose that Alice & Bob have agreed upon three n-bit numbers
a < b < c, the cards. They want to randomly choose one card
each so that the following holds:
1 Their cards are different
2 All six pairs of distinct cards are equiprobable as outcomes
3 Alice’s card is known to Alice but not to Bob, similarly to Bob
4 Since the person with the highest card wins the game, the
outcome should be indisputable
This protocol can be achieved by cryptographic techniques.
Shamir, Rivest,
Adleman - Mental poker - The mathematical gardener,
pp.37, 1981

29. Protocols
Mental Poker protocol
First the two players agree on a large prime number p, and each
has two secret keys, an encryption key eAlice, eBob and a
decryption key dAlice, dBob. Alice is the dealer, she encrypts the
three cards and sends to Bob the encrypted message aeAlice
mod p, beAlice mod p, ceAlice mod p. Bob then picks one of the
three messages and returns it to Alice, who decodes it and keeps it
as her card. Bob’s selection must be random. Bob then encrypts
the two remaining cards a and c with his encryption key to obtain
aeAlice eBob mod p, ceAlice eBob mod p and sends a random
permutation of the result to Alice. Alicenow picks one of these
messages, say a, decodes it with her key dAlice, and sends the
result aeBob mod p to Bob. Bob decrypts it using dBob and the
protocol terminates.