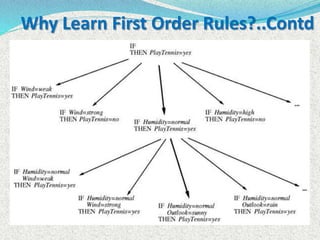
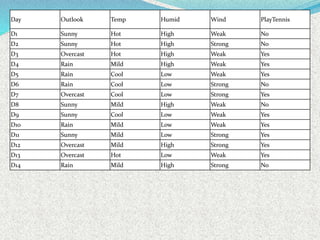
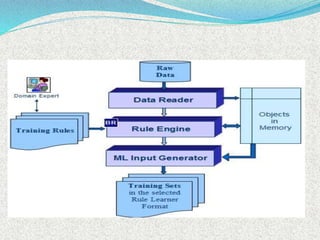
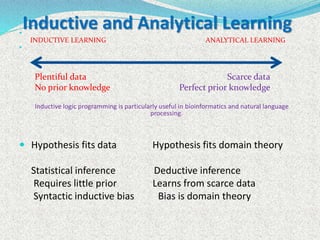
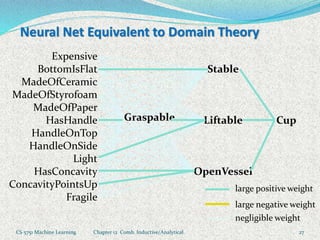
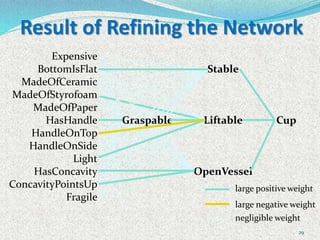
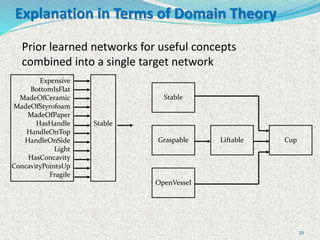
The document discusses machine learning algorithms for learning first-order logic rules from examples. It introduces the FOIL algorithm, which extends propositional rule learning algorithms like sequential covering to learn more general first-order Horn clauses. FOIL uses an iterative specialization approach, starting with a general rule and greedily adding literals to better fit examples while avoiding negative examples. The document also discusses how combining inductive learning with analytical domain knowledge can improve learning, such as in the KBANN approach where a neural network is initialized based on the domain theory before training on examples.

1. Dr.M.Bindhu
Associate Professor/ECE
Saveetha Engineering
College

2. OUTLINE
Machine Learning (AI) –Learning Rules
Sequential Covering Algorithm
Learn One Rule
Why Learn First Order Rules?
 First Order Logic: Terminology
 The FOIL Algorithm
 Why Combine Inductive And Analytical Learning?
 Kbann: Prior Knowledge To Initialize The Hypothesis
 Tangentprop, EBNN: Prior Knowledge Alters Search
Objective
 FOCL Algorithm : Prior Knowledge Alters Search
Operators

3. Machine Learning (AI)
A key aspect of intelligence is the ability to
learn knowledge over time.
Vast majority of machine learning algorithm
have been developed to learn knowledge
that is inherently propositional, where the
domain of interest is encoded in terms of a
fixed set of variables.
 Subfield of symbolic artificial
intelligence which uses logic programming as
a uniform representation for examples,
background knowledge and hypotheses

5.  https://youtu.be/ad79nYk2keg

6. We can learn sets of rules and
then converting the tree to rules.
We can also use a genetic algorithm
that encodes the rules as bit strings.
But, these only work with predicate
rules (no variables).
They also consider the set of rules as
a whole, not one rule at a time.
LEARNING RULES

7. SEQUENTIAL COVERING ALGORITHM
1..Learn one rule with high accuracy, any coverage
2. Remove positive examples covered by this rule
3. Repeat
Example:
Wind(d1)= Strong, Humdity(d1)=Low, Outlook(d1)=Sunny, PlayTennis(d1)=No
Wind(d2)= Weak, Humdity(d2)=Med, Outlook(d2)=Sunny, PlayTennis(d2)=Yes
Wind(d3)=Med, Humdity(d3)=Med, Outlook(d3)=Rain, PlayTennis(d3)=No
Target_attribute is the one wish to learn. e.g. PlayTennis(x)
Attributes is the set of all possible attributes.
e.g. Wind(x), Humidity(x), Outlook(x) threshold is the desired

8. SEQUENTIAL COVERING ALGORITHM
Sequential_covering (Target_attribute, Attributes, Examples,
Threshold) :
Learned_rules = {}
Rule = Learn-One-Rule(Target_attribute, Attributes,
Examples)
while Performance(Rule, Examples) > Threshold :
Learned_rules = Learned_rules + Rule
Examples = Examples - {examples correctly classified by
Rule}
Rule = Learn-One-Rule(Target_attribute, Attributes,
Examples)
Learned_rules = sort Learned_rules according to
performance over Examples
return Learned_rules

9. Drawback Of Sequential Covering
Algorithm
We require Learn-One-Rule to have
high (perfect?) accuracy but not
necessarily high coverage (i.e., when it
makes a prediction it should be true).
Since it performs a greedy search it is
not guaranteed to find the best or
smallest set of rules that cover the
training examples.

10. Why Learn First Order Rules?
Propositional logic allows the expression of individual
propositions and their truth-functional combination.
1.Propositions like Tom is a man or All men are mortal may be
represented by single proposition letters such as P or Q
2. Truth functional combinations are built up using connectives,
such as ∧, ∨, ¬, →
Example:
P∧Q
 Inference rules defined over propositional forms,P → Q
P is Tom is a man and Q is All men are mortal,
Inference that Tom is mortal does not follow in propositional
logic

11. Why Learn First Order Rules?..Contd
First order logic allows the expression of propositions and
their truth functional combination, but it also allows us
to represent propositions as assertions of predicates
about individuals or sets of individuals.
Example:
Propositions like Tom is a man or All men are mortal
may be represented by predicate-argument
representations such as man(tom) or ∀x(man(x) →
mortal(x)) (so, variables range over individuals) .
Inference rules permit conclusions to be drawn about
sets/individuals – e.g. mortal(tom)

12. Why Learn First Order Rules?..Contd

13. Day Outlook Temp Humid Wind PlayTennis
D1 Sunny Hot High Weak No
D2 Sunny Hot High Strong No
D3 Overcast Hot High Weak Yes
D4 Rain Mild High Weak Yes
D5 Rain Cool Low Weak Yes
D6 Rain Cool Low Strong No
D7 Overcast Cool Low Strong Yes
D8 Sunny Mild High Weak No
D9 Sunny Cool Low Weak Yes
D10 Rain Mild Low Weak Yes
D11 Sunny Mild Low Strong Yes
D12 Overcast Mild High Strong Yes
D13 Overcast Hot Low Weak Yes
D14 Rain Mild High Strong No

14. Learn-One-Rule
P os positive Examples
N eg negative Examples
while P os,
Learn a N ewRule
{ N ewRule most general rule possible
N ewRule N eg
N eg { while N ewRuleN eg, do
Add a new literal to specialize N ewRule
1. Candidate literals generate candidates
2.Best literal argmaxL2Candidate literals P erf
ormance(SpecializeRule(N ewRule; L))
3. add Best literal to N ewRule preconditions
4. N ewRule N eg subset of N ewRuleN eg
that satises N ewRule preconditions
{ Learned rules Learned rules + N ewRule
{ P os P os fmembers of P os covered by N ewRuleg
Return Learned rule

15. Autonomous Car Technology
Laser Terrain
Mapping
Stanley
Learning from Human
Drivers
Sebastian
Adaptive
Vision
Pat
h
Plannin
g
Images and movies taken from Sebastian Thrun’smultimedia
w1e4bsite.

16. Idea: organize the hypothesis space search
in general to specific fashion.
Start with most general rule
precondition, then greedily add the
attribute that most improves performance
measured over the training examples.
Can be generalized to multi-valued target
functions.
There are other ways to define Performance(),
besides using entropy.
Learn One Summary

18. First-Order Logic Definitions
 Every expression is composed
of constants, variables, predicates, and functions.
 A term is any constant, or variable, or any function
applied to any term.
 A literal is any predicate (or its negation) applied to
any set of terms.Female(Mary), ¬Female(x)
 A ground literal is a literal that does not contain any
variables.
 A clause is any disjunction of literals whose variables
are universally quantified.∀ x : Female(x) ∨ Male(x)
 A Horn clause is an expression of the form H ← L1 ∧
L2 ∧ ... ∧ Ln

19. First Order Logic: Terminology
 – constants – e.g. bob, 23, a
 – variables – e.g. X,Y,Z
– predicate symbols – e.g. female, father
– predicates take on the values True or False
only
 – function symbols – e.g. Age – functions
can take on any constant as a value
 – connectives – e.g. ∧, ∨, ¬, → (or ←)
– quantifiers – e.g. ∀, ∃

20.  A term is
 – any constant – e.g. bob
 – any variable – e.g X
 – any function applied to any term – e.g. age(bob)
 A literal is any predicate or negated predicate applied
to any terms – e.g. f emale(sue), ¬f ather(X,Y)
 – A ground literal is a literal that contains no variables
– e.g. f emale(sue)
 – A positive literal is a literal that does not contain a
negated predicate – e.g. f emale(sue)
 – A negative literal is a literal that contains a negated
predicate – e.g ¬f ather(X,Y)

21. Learning First-Order Horn Clauses
 Say we are trying to learn the concept Daughter(x,y) from
examples.
 Each person is described by the attributes: Name, Mother,
Father, Male, Female.
 Each example is a pair of instances,
 say a and b:
 Name(a) = Sharon, Mother(a) = Louise, Father(a) = Bob,
Male(a) = False, Female(a) = True
Name(b) = Bob, Mother(b) = Nora, Father(b) = Victor,
Male(b) = True, Female(b) = False, Daughter(a,b) = True
 If we give a bunch of these examples to CN2 or C4.5 they
will output a set of rules like:IF Father(a) = Bob ∧ Name(b)
= Bob ∧ Female(a) THEN Daughter(a,b)
 A first-order learner would output more general rules
likeIF Father(x) = y ∧ Female(x) THEN Daughter(x,y)

22. FOIL ALGORITHM
FOIL extends the SEQUENTIAL-COVERING and
LEARN-ONE-RULE algorithms for propositional
rule learning to first order rule learning
 • FOIL learns in two phases:
an outer loop which acquires a disjunction of
Horn clause-like rules which together cover the
positive examples
 an inner loop which constructs individual rules
by progressive specialisation of a rule through
adding new literals selected until no negative
examples are covered.

23. FOIL(T arget predicate; P redicates; Examples)
P os positive Examples
N eg negative Examples
while P os, do
Learn a N ewRule
N ewRule most general rule possible
N ewRuleN eg N eg
while N ewRuleN eg, do
Add a new literal to specialize N ewRule
1. Candidate literals generate candidates
2. Best literal argmaxL2Candidate literals F oil Gain(L; N ewRule)
3. add Best literal to N ewRule preconditions
4. N ewRuleN eg subset of N ewRuleN eg that satisfiesN ewRule
preconditions
Learned rules Learned rules + N ewRule
P os P os -members of P os covered by N ewRuleg
Return Learned rule

24. Inductive and Analytical Learning
INDUCTIVE LEARNING ANALYTICAL LEARNING

Inductive logic programming is particularly useful in bioinformatics and natural language
processing.
 Hypothesis fits data Hypothesis fits domain theory
Statistical inference Deductive inference
Requires little prior Learns from scarce data
Syntactic inductive bias Bias is domain theory
Plentiful data
No prior knowledge
Scarce data
Perfect prior knowledge

25. 25
Domain Theory
Cup  Stable, Liftable, OpenVessel
Stable  BottomIsFlat
Liftable  Graspable, Light
Graspable  HasHandle
OpenVessel  HasConcavity, ConcavityPointsUp
Cup
Stable Liftable OpenVessel
Graspable
BottomIsFlatLight HasConcavityConcavityPointsUpHasHandle

26. 26
KBANN
Knowledge Based Artificial Neural Networks
KBANN (data D, domain theory B)
1. Create a feed forward network h equivalent to B
2. Use BACKPROP to tune h to fit D

27. CS 5751 Machine Learning Chapter 12 Comb. Inductive/Analytical 27
Neural Net Equivalent to Domain Theory
Expensive
BottomIsFlat
MadeOfCeramic
MadeOfStyrofoam
MadeOfPaper
HasHandle
HandleOnTop
HandleOnSide
Light
HasConcavity
ConcavityPointsUp
Fragile
Stable
Liftable
OpenVessel
CupGraspable
large positive weight
large negative weight
negligible weight

28. 28
Creating Network Equivalent to Domain
Theory
Create one unit per horn clause rule (an AND unit)
Connect unit inputs to corresponding clause
antecedents
For each non-negated antecedent, corresponding input
weight w  W, where W is some constant
For each negated antecedent, weight w  -W
Threshold weight w0  -(n - .5) W, where n is number
of non-negated antecedents
Finally, add additional connections with near-zero
weights
Liftable  Graspable, ¬Heavy

29. 29
Result of Refining the Network
Expensive
BottomIsFlat
MadeOfCeramic
MadeOfStyrofoam
MadeOfPaper
HasHandle
HandleOnTop
HandleOnSide
Light
HasConcavity
ConcavityPointsUp
Fragile
Stable
Liftable
OpenVessel
CupGraspable
large positive weight
large negative weight
negligible weight

30. 30
Hypothesis Space Search in KBANN
Hypotheses that
fit training data
equally well
Initial hypothesis
for KBANN
Initial hypothesis
for Backpropagation
Hypothesis Space

31. 31
EBNN
Explanation Based Neural Network
Key idea:
Previously learned approximate domain
theory
Domain theory represented by collection
of neural networks
Learn target function as another neural
network

32. 32
Expensive
BottomIsFlat
MadeOfCeramic
MadeOfStyrofoam
MadeOfPaper
HasHandle
HandleOnTop
HandleOnSide
Light
HasConcavity
ConcavityPointsUp
Fragile
Stable
Explanation in Terms of Domain Theory
Prior learned networks for useful concepts
combined into a single target network
Graspable
Stable
OpenVessel
Liftable Cup

33. 33
Hypothesis Space Search in TangentProp
Hypotheses that
maximize fit to data
TangetProp
Search
Backpropagation
Search
Hypothesis Space
Hypotheses that
maximize fit to
data and prior
knowledge

34. 34
FOCL algorithm (First Order Combined
Learner)
Adaptation of FOIL that uses domain theory
When adding a literal to a rule, not only consider
adding single terms, but also think about adding terms
from domain theory
Most importantly a potentially incorrect hypothesis is
allowed as an initial approximation to the predicate
to be learned. The main goal of FOCL is to incorporate
the methods of explanation-based learning (EBL)

35. 35
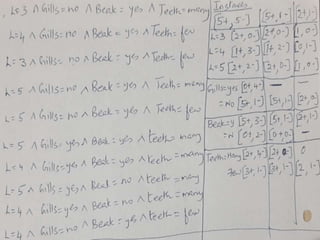
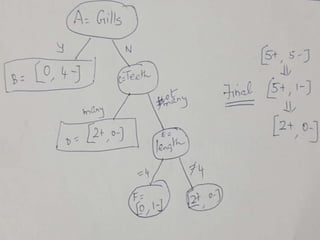
Search in FOCL
Cup  HasHandle
[2+,3-]
Cup 
Cup  ¬HasHandle
[2+,3-]
Cup  Fragile
[2+,4-]
Cup  BottomIsFlat,
Light,
HasConcavity,
ConcavityPointsUp
[4+,2-]
...
Cup  BottomIsFlat,
Light,
HasConcavity,
ConcavityPointsUp,
HandleOnTop
[0+,2-]
Cup  BottomIsFlat,
Light,
HasConcavity,
ConcavityPointsUp,
¬ HandleOnTop
[4+,0-]
Cup  BottomIsFlat,
Light,
HasConcavity,
ConcavityPointsUp,
HandleOnSide
[2+,0-]
...

36. 36
FOCL Results
Recognizing legal chess endgame positions:
30 positive, 30 negative examples
FOIL: 86%
FOCL: 94% (using domain theory with 76%
accuracy)
NYNEX telephone network diagnosis
500 training examples
FOIL: 90%
FOCL: 98% (using domain theory with 95%
accuracy)

37. VIDEO LINK
 https://www.youtube.com/watch?v=rVlN0ZCYmtI
 https://www.youtube.com/watch?v=SSrD02pdE78

38. RECAP
Sequential Covering Algorithm
Learn One Rule
The FOIL Algorithm
 FOCL Algorithm

39. http://jmvidal.cse.sc.edu/talks/learningrules/allslides.xml
http://www.cs.cmu.edu/afs/cs.cmu.edu/project/theo-
20/www/mlbook/ch10.pdf
https://bcssp10.files.wordpress.com/2013/02/lecture151.pdf
REFERENCES
Machine learnning ---Tom Mitchell (1998):

43. HEARTFUL
THANK YOU