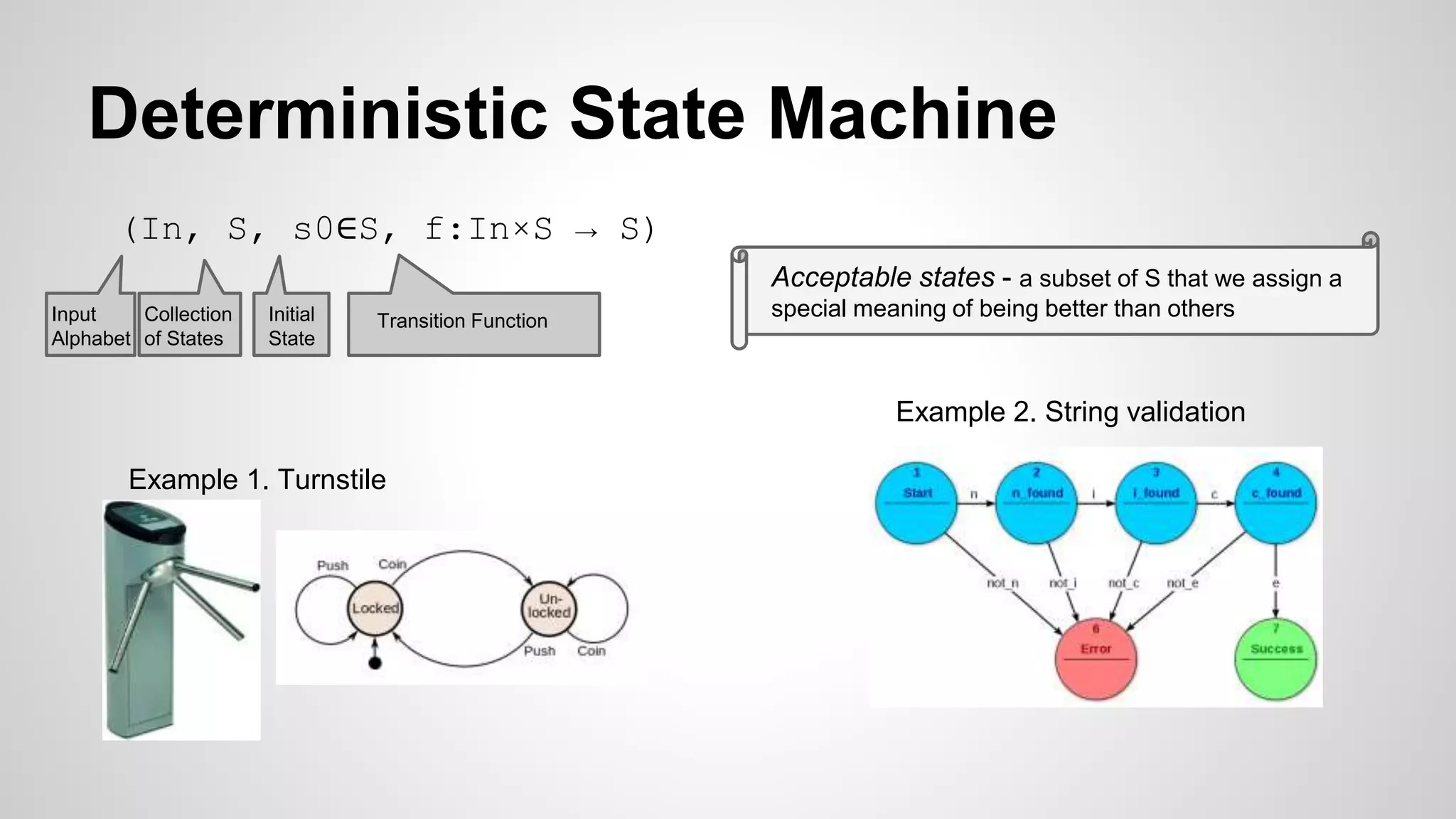
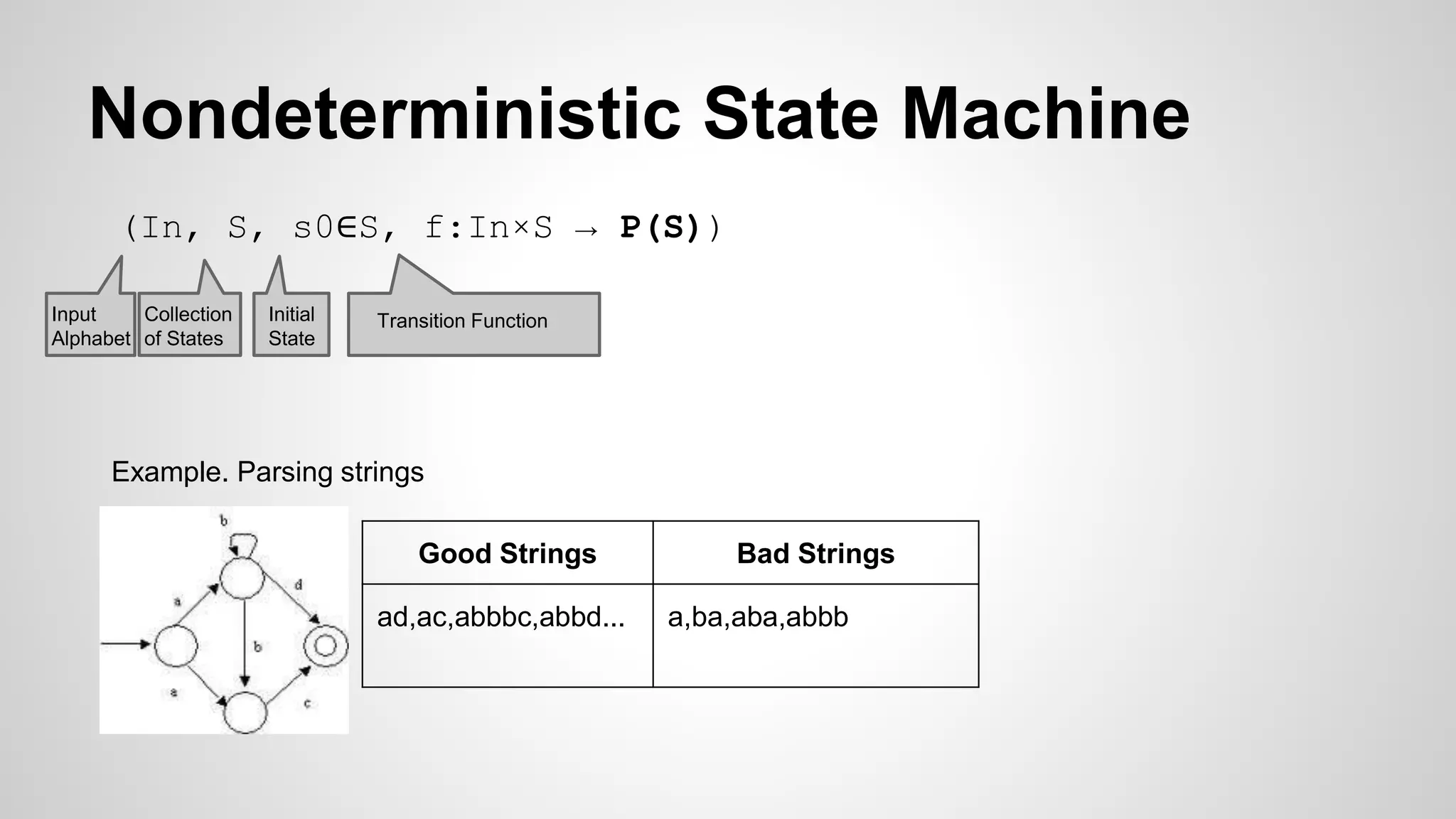
The document discusses formal methods in software, focusing on deterministic and nondeterministic finite state machines (FSMs), their definitions, and examples. It introduces the concepts of transitions, acceptable states, and the relationship between regular languages and FSMs, including how to construct regular languages and grammars. Additionally, it covers the complexities of parsing regular expressions and various illustrative examples and references.

1. Formal Methods in
Software
Lecture 2. Languages and Machines-1
Vlad Patryshev
SCU
2014

2. Deterministic State Machine
(In, S, s0∈S, f:In×S → S)
Input
Alphabet
Collection
of States
Initial
State
Transition Function
Example 1. Turnstile
Example 2. String validation
Acceptable states - a subset of S that we assign a
special meaning of being better than others

3. We Have Monoids, actually
• Alphabet A gives a monoid In=A*: all strings in A, including empty
• Having f: A*×S → S is equivalent to having f’: A* → SS
(where SS is all functions S→S, that is, all transitions)
• SS is a monoid (identity function and composition)
• f’ is a monoidal function

4. Nondeterministic State Machine
(In, S, s0∈S, f:In×S → P(S))
Input
Alphabet
Collection
of States
Initial
State
Transition Function
Example. Parsing strings
Good Strings Bad Strings
ad,ac,abbbc,abbd... a,ba,aba,abbb

5. Terminology and TLA/FLA
• FSM - finite state machine (finite number of states)
• DFA - deterministic finite automaton, aka deterministic FSM
• NFA - non-determinisitic FSM
• Acceptable States - a subset of S that we assign a special meaning of
being better than others
• Input Language - strings built of Input Alphabet
• ε, Empty Symbol - empty string (a word in Input Language)
• Regular Language is an input language accepted by an FSM

6. NFA ↔ DFA
1. DFA is a special case of NFA (every transition is to a singleton)
2. NFA → DFA?
NFA X = (In, S, s0∈S, f:In×S → P(S))
DFX PX = (In, P(S), {s0}∈P(S), f’:In×P(S) → P(S))
where f’(a,B) = ∪{f(a,b)|b∈B}

7. NFA → DFA, Example

8. Regular Languages
Example: a, aa, aaa, aaaa…
Counterexample: anbn (for all n)
Regular language is a language accepted by an FSM
Given an FSM, its language is the language accepted by this FSM
Given an alphabet A, a language is a set of words in A
(in other words, a subset of A*)

9. Building Regular Languages
• Empty language ∅ is regular (its FSM accepts nothing)
• Singleton {a} is regular (its FSM takes a once)
• Union of two languages, A∪B, is regular:
• Concatenation of two languages, A·B, is regular:
• If A is regular, A* is regular:

10. Formal Grammar
Given an alphabet A, and a language L⊂A*, try to define it via formal
grammar.
(A, N, S∈N, Rules)
Rules: each rule looks like x1x2...xkzxk+1...xn→ y1y2...ym, where
xi∈(A∪N), yi∈(A∪N), z∈N
“Terminal symbols” Nonterminal symbols
Start symbol

11. Example of Formal Grammar
D → 0
D → 1
N → D
N → DN
S → N
S → X+X
S → X-X
P → S
P → (P)
P → P*P
X → P
X → S
e.g. (0100-0*11)*(111+1-0)

12. Example in Backus-Naur Form (BNF)
<D> ::= 0|1
<N> ::= <D>|<D><N>
<S> ::= <N>|<X>+<X>|<X>-<X>
<P> ::= <S>|(<S>)|<P>*<P>
<X> ::= <P>|<S>
e.g. (0100-0*11)*(111+1-0)

13. Grammar of Regular Language
Given an alphabet A, and a regular language L⊂A*, its grammar has a very
simple form:
● B → ε
● B → a
● B → aC
where B and C are nonterminal symbols, a is some terminal symbol.

14. Regular Expressions
/abc*d?..e/ -- matches abxye, abccccdabe and the like
R → aR1
R1 → bR2
R2 → cR2
R2 → R3
R2 → dR3
R3 → (anything)R4
R4 → (anything)R5
R5 → e

15. Parsing Regular Expressions
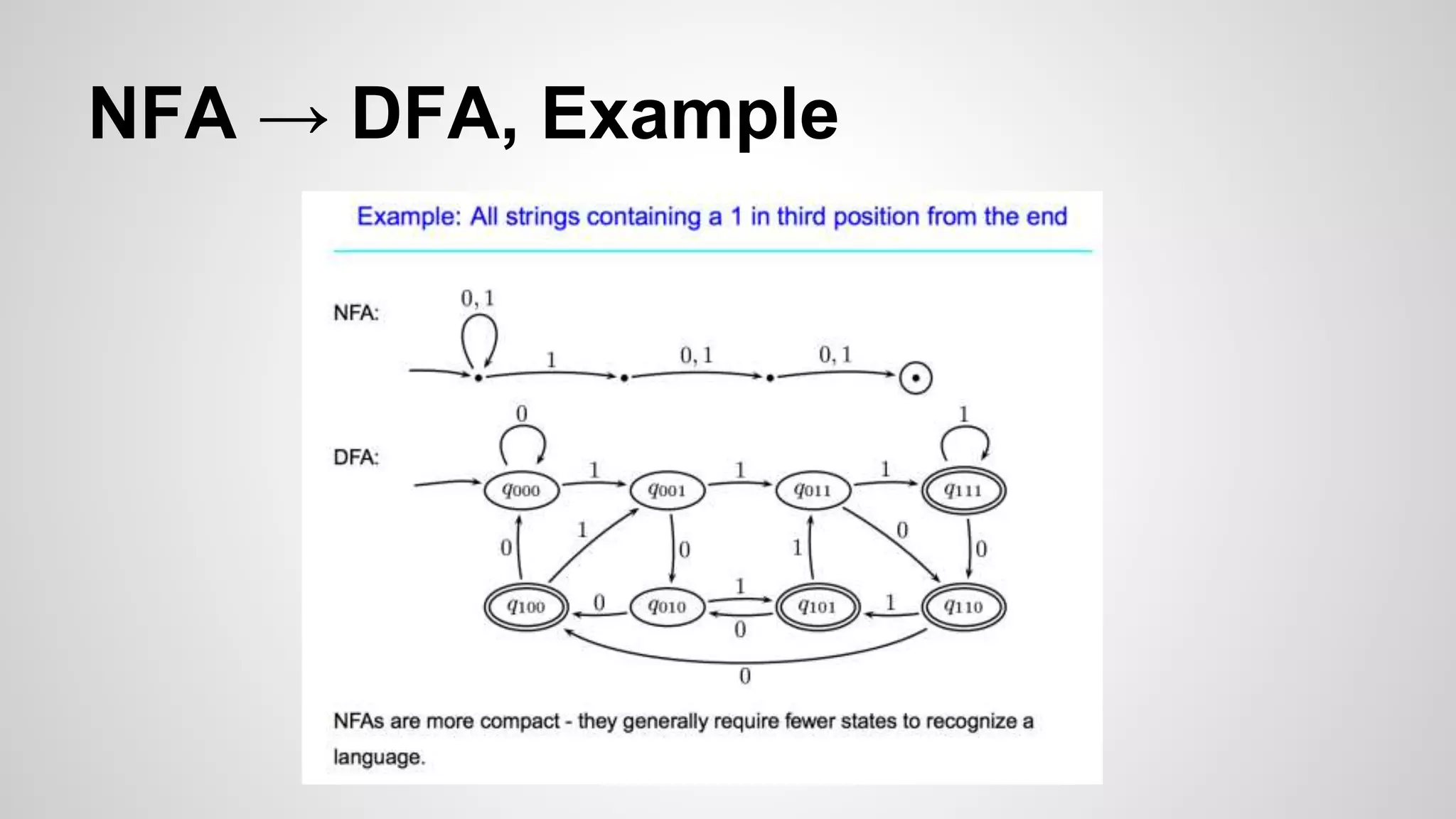
The problem with NFA - exponential time, O(2n). E.g. a?nan against an
Can transform to DFA;
then it’s linear,
O(n) (but may take space).
A simple example in Scala: https://gist.github.com/vpatryshev/3778294
The example is tricky: it’s not an FSM; it uses call stack.
main(int c,char**v){return!m(v[1],v[2]);}m(char*s,char*t){return*t-42?*s?63==*t|*s==*t&&m(s+1,t+1):!*t:m(s,t+1)||*s&&m(s+1,t);}

16. Big O
f(x) = O(g(x)) for x → ∞
means this:
∃x0∃C ∀x>x0 |f(x)/g(x)| < C
E.g.
ax2+bx+c = O(x2)
1/x = O(1)
n! = O((n/2)n)

17. References
http://www.cs.ox.ac.uk/people/luke.ong/personal/teaching/moc/nfa2up.pdf
http://swtch.com/~rsc/regexp/regexp1.html
https://gist.github.com/vpatryshev/3778294
Wikipedia