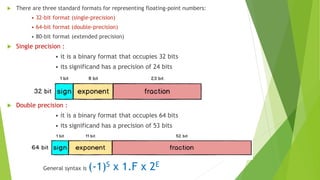
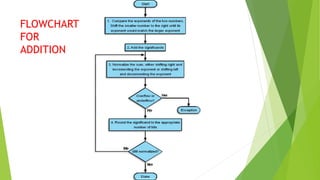
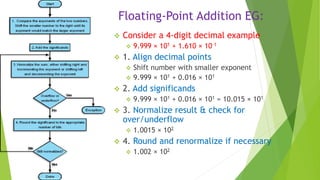
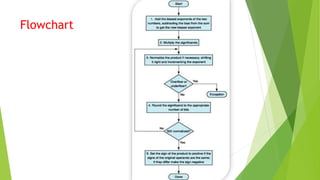
The document reviews fixed-point and floating-point number representations in computer architecture, highlighting their range, overflow susceptibility, and unique formats. It explains that fixed-point numbers have a fixed number of digits after the decimal, while floating-point numbers can represent a wider range using scientific notation, normalized forms, and biases. The document also details the processes for adding and multiplying floating-point numbers, including rounding techniques and the use of guard, round, and sticky bits.

1. Computer
Architecture & organization
ALU
S.CIYAMALA KUSHBU
ASSISTANT PROFESSOR/ECE

2. REVIEW OF FIXED POINT NUMBERS
Limited in the range of numbers or the fractional
number with fixed digits after radix point.
Eg: 125.25,12345.89,10101.1010
 Susceptible to problems of overflow.
In a fixed-point processor, numbers are
represented in integer format.

3. FLOATING POINT NUMBER
 Larger in the range of numbers or the fractional number with varying digits
after radix point.
Eg:1234565633.33333, 987891.23456789 etc ..
 Represented in scientific notation format.
 General syntax for floating point number can given as
M x BE
M -value of significand or Mantissa(takes +ve or –ve sign)
B- Base
E-Exponent(takes +ve or –ve sign)
(i.e)The above example can be represented as 1.23*10^9 and 98.80*10^4.
 Representation of floating point is not unique.
Eg:66.55 can be represented as 6.655*10^1 or 0.665*10^2or 0.06655*10^3.

4. Normalizing Floating Point Data
 Exactly one non-zero digit should appear before the radix
point
In a decimal number, this digit can be from 1 to 9.
In a binary number, this digit should be 1.
Normalized FP Numbers:
Binary FP Normalization:
 Since the most significant bit is always 1 in binary, we can
assume that it is implied and that we do not actually have to
represent it.

5.  There are three standard formats for representing floating-point numbers:
• 32-bit format (single-precision)
• 64-bit format (double-precision)
• 80-bit format (extended precision)
 Single precision :
• it is a binary format that occupies 32 bits
• its significand has a precision of 24 bits
 Double precision :
• it is a binary format that occupies 64 bits
• its significand has a precision of 53 bits
General syntax is (-1)S x 1.F x 2E

11. Floating point Addition

12. FLOWCHART
FOR
ADDITION

13. Floating-Point Addition EG:
 Consider a 4-digit decimal example
 9.999 × 101 + 1.610 × 10–1
 1. Align decimal points
 Shift number with smaller exponent
 9.999 × 101 + 0.016 × 101
 2. Add significands
 9.999 × 101 + 0.016 × 101 = 10.015 × 101
 3. Normalize result & check for
over/underflow
 1.0015 × 102
 4. Round and renormalize if necessary
 1.002 × 102

14. Floating-Point Binary Addition EG:
Now consider a 4-digit binary example
0.5 + –0.4375
0.5)ten = 0.1)two x 20 = 1.000)two x 2-1
adding bias gives: 1.000 x 2126
–0.4375 )ten = -0.0111 )two x20 = -1.110 )two x 2-2
adding bias gives: -1.110 x 2125
1. Align binary points
-1.110 x 2125 = -0.111x2126
2. Add significands
1.0 x2126 + (-0.111x2126 ) = 0.001 x 2126
3. Normalize result & check for over/underflow
1.0002 × 2–123 (with no over/underflow since biased
exponent is between 0 and 255)
4. Round and renormalize if necessary
No need to, it fits in 4 bits.
Final answer with bias removed is: 1.000 x 2(123-127) =
1.000 x 2-4 = 0.0625)ten

15. Floating point Multiplication

16. Flowchart

17. Rounding
Guard, Round and Sticky digit/bit
Guard digit: first extra digit/bit to the right of mantissa --
used for rounding addition results
Round digit: second extra digit/bit to the right of
mantissa -- used for rounding multiplication results
Sticky bit: third extra digit/bit to the right of mantissa –
used for resolving ties such as 0.50...00 vs. 0.50...01

18. Rounding examples
• An example without guard and round digits
– Add 9.76 x 1025 and 2.59 x 1024 assuming 3 digit mantissa
• Shift mantissa of the smaller number to the right: 0.25 x 1025
• Add mantissas: 10.01x 1025
• Check and normalize mantissa if necessary: 1.00x 1026
• An example with guard and round digits
– Add 9.76 x 1025 and 2.59 x 1024 assuming 3 digit mantissa
• Internal registers have extra two digits: 9.7600 x 1025 and 2.5900
x 1024
• Shift mantissa of the smaller number to the right: 0.2590 x 1025
• Add mantissas: 10.0190 x 1025
• Check and normalize mantissa if necessary: 1.0019 x 1026
• Round the result: 1.00 x 1026

19. Rounding examples
• An example without guard and round digits
– Add 9.78 x 1025 and 8.79 x 1024 assuming 3 digit mantissa
• Shift mantissa of the smaller number to the right: 0.87 x 1025
• Add mantissas: 10.65 x 1025
• Normalize mantissa if necessary: 1.06 x 1026
• An example with guard and round digits
– Add 9.78 x 1025 and 8.79 x 1024 assuming 3 digit mantissa
• Internal registers have extra two digits: 9.7800 x 1025 and
8.7900 x 1024
• Shift mantissa of the smaller number to the right: 0.8790 x 1025
• Add mantissas (note extra digit on the left): 10.6590 x 1025
• Check and normalize mantissa if necessary: 1.0659 x 1026
• Round the result: 1.07 x 1026

20. THANK YOU