This document describes the design and implementation of a 32-bit floating point adder according to the IEEE 754 standard using VHDL. It includes block diagrams of the main components: a pre-adder block to prepare the operands, an adder block to perform the addition or subtraction, and a standardization block to normalize the result. It also provides details on the steps involved, including extracting the sign, exponent and mantissa of the operands, handling special cases like zero, infinity and NaN, aligning the exponents, performing the addition or subtraction, normalizing and rounding the result, and adjusting the exponent.

1. A FLOATING-POINT ADDER (IEEE 754
FLOATING-POINT SINGLE-PRECISION 32-BIT
FORMAT)
B Y N I V E D I T A A C H A R Y Y A

2. ABSTRACT
Floating Point arithmetic is by far the most used way of approximating real
number arithmetic for performing numerical calculations on modern
computers. The advantage of floating-point representation over fixed-point
and integer representation is that it can support a much wider range of
values. Addition/subtaraction,Multiplication and division are the common
arithmetic operations in these computations.Among them Floating point
Addition/Subtraction is the most complex one.This paper implements an
efficient 32bit floating point adder according to ieee 754 standard with
optimal chip area and high performance using VHDL .The proposed
architecture is implemented on Xilinx ISE Simulator.Results of proposed
architecture are compared with the existed architecture and have observed
reduction in area and delay . Further, this project can be extendable by
using any other type of faster adder in terms of area, speed and power.

3. BLOCK DIAGRAM
The main idea has been described before. Once the different steps to follow have
been explained it is time to start to think in the code implementation.
In this subsection a first block diagram –as a draft- will be made. It still does not
go into the most difficult points because in the next section, once a division of
the project in three parts will be done, a complete description of each step will be
performed.
These three parts are as follows:
• Pre-Adder Block
• Adder Block
• Standardizing Block
They make reference to the three main processes of the project. First the
numbers should be treated (pre-adder) in order to perform the operation
properly (adder) and finally, standardizing the result according with the standard
IEEE 754 (standardizing).

5. OPERATION
Following the established plan, the way to do the operations
(addition/subtraction) will be set.
This point will be also used to try to explain why these steps are necessary
in
order to make clearer and easier the explanation of the code in the next
section.
The different steps are as follows:
1. Extracting signs, exponents and mantissas of both A and B numbers. As
it has
been said, the numbers format is as follows:

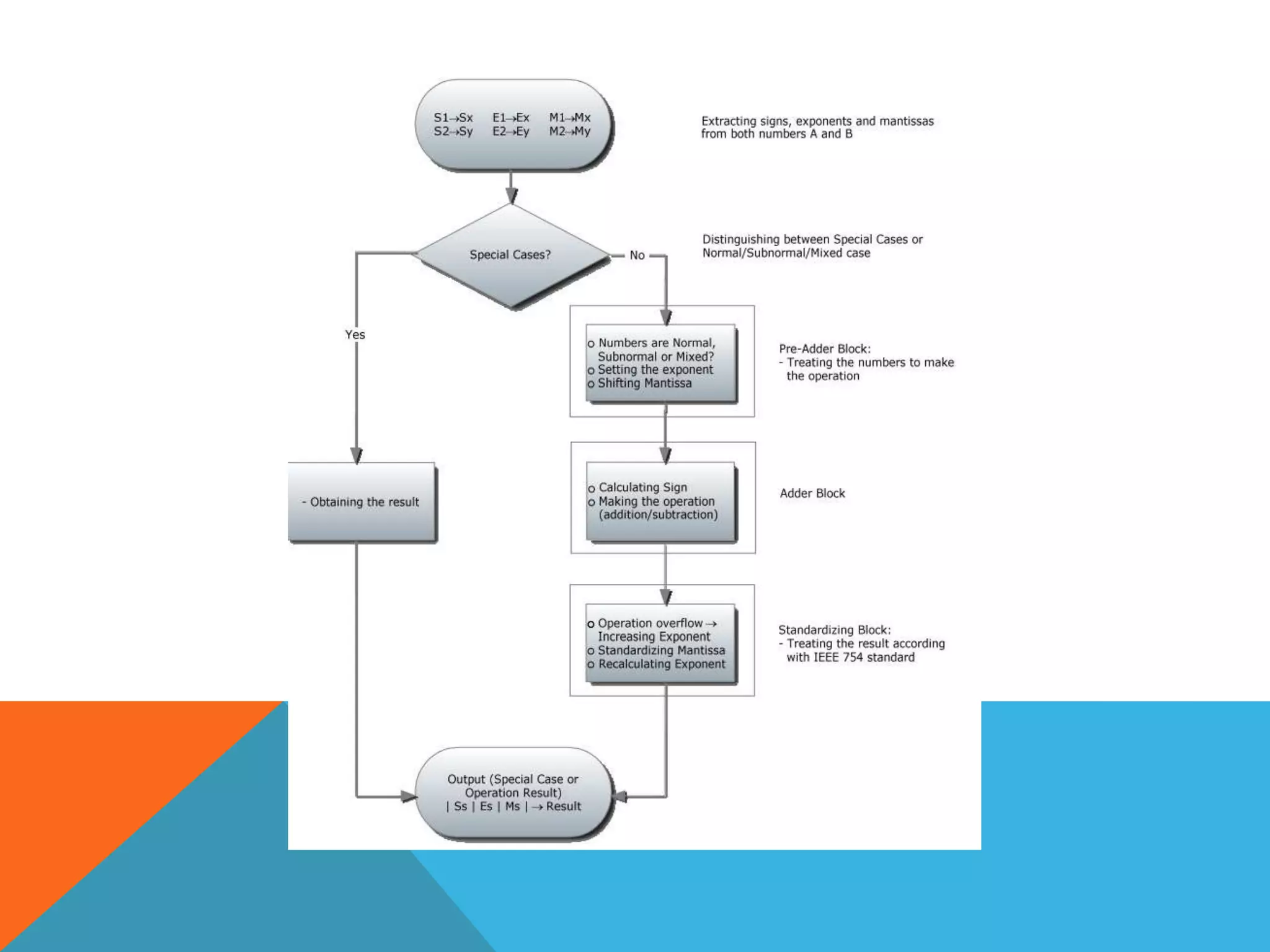
6. Then the first step is finding these values.
2. Treating the special cases:
• Operations with A or B equal to zero
• Operations with ±∞
• Operations with NaN
3. Finding out what type of numbers are given:
• Normal
• Subnormal
• Mixed
4. Shifting the lower exponent number mantissa to the right [Exp1− Exp2] bits.
Setting the output exponent as the highest exponent.

7. 5. Working with the operation symbol and both signs to calculate the output sign
and determine the operation to do

8. 6. Addition/Subtraction of the numbers and detection of mantissa overflow
(carry bit)
7. Standardizing mantissa shifting it to the left up the first one will be
at the first
position and updating the value of the exponent according with the
carry bit
and the shifting over the mantissa.
8. Detecting exponent overflow or underflow (result NaN or ±∞)

9. WORKING
The IEEE 754 Single Precision Binary Format is as shown below:-
Following are the steps for Converting a decimal number to floating point number
:-
1. Convert a Decimal number to Binary number
(975.75)10 = (1111001111.11)2
2. Normalize the number
1.11100111111* 29
3. From this normalized number we can fill all 32-bits of floating point number
Sign bit = 0 (number is positive)
4. Exponent = Bias + 9 = 127 + 9 = (136)10 = (1000 1000)2
5. Fraction part will contain all the bits after decimal point.
6. (975.75)10 is expressed as shown below in single precision floating point
format.

10. FLOWCHART

11. A description of the proposed implementation algorithm is as follows:-
1. The two operands, N1 and N2 are read in and compared for denormalization and infinity. If numbers
are
denormalized , set the implicit bit to 0 otherwise it is set to 1. At this point, the fraction part is
extended to
24 bits.
2. The two exponents, e1 and e2 are compared using 8-bit subtraction. If e1 is less than e2, N1 and N2
are
swapped i.e. previous f2 will now be referred to as f1 and vice versa.
3. The smaller fraction, f2 is shifted right by the absolute difference result of the two exponents‟
subtraction.
Now both the numbers have the same exponent.
4. The two signs are used to see whether the operation is a subtraction or an addition.
5. If the operation is a subtraction, the bits of the f2 are inverted.
6. Now the two fractions are added using a 2‟s complement adder.
7. If the result sum is a negative number, it has to be inverted and a 1 has to be added to the result.
8. The result is then passed through a leading one detector or leading zero counter. This is the first
step in the
normalization step.
9. Using the results from the leading one detector, the result is then shifted left to be normalized. In
some cases,
1-bit riht shift is needed.
10. The result is then rounded towards nearest even, the default rounding mode.
11. If the carry out from the rounding adder is 1, the result is left shifted by one.
12. Using the results from the leading one detector, the exponent is adjusted. The sign is computed
and after