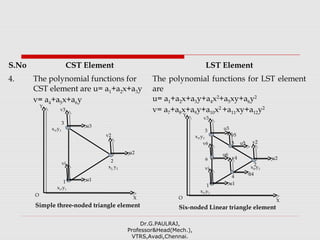
The document discusses two-dimensional finite element analysis. It describes triangular and quadrilateral elements used for 2D problems. The derivation of the stiffness matrix is shown for a three-noded triangular element. Shape functions are presented for triangular and quadrilateral elements. Examples are provided to calculate strains for a triangular element and to determine temperatures at interior points using shape functions.

1. TO
ByBy
Dr.G.PAULRAJDr.G.PAULRAJ
Professor & HeadProfessor & Head
Department of Mechanical EngineeringDepartment of Mechanical Engineering
Vel Tech (Owned by RS Trust)Vel Tech (Owned by RS Trust)
Chennai-600 062.Chennai-600 062.

2. Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
UNIT-III TWO DIMENSIONAL
SCALAR VARIABLE PROBLEMS

3. UNIT III TWO DIMENSIONAL
SCALAR VARIABLE PROBLEMS
 Second Order 2D Equations involving Scalar
Variable Functions – Variational formulation –
Finite Element formulation – Triangular
elements – Shape functions and element
matrices and vectors. Application to Field
Problems - Thermal problems – Torsion of Non
circular shafts –Quadrilateral elements – Higher
Order Elements.
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

4. TWO DIMENSIONAL (2-D)
ANALYSIS
 For example a slender bar of uniform C-S, to make reasonable assumption that
the deflection varies in a known way across the C-S.
 Many a time, complex real life structures such as a gear tooth or a thick pressure
vessel or a crank shaft, the unknown field variables vary independently along
two or even three dimensions and to make any suitable assumption about their
variation.
 For a block of material of comparable dimension, for example, the heat transfer is
more closely approximated as 3-D rather than as 1-D or 2-D.
 While every real-life problem can be modeled as a 3-D problem, it may be very
expensive to perform such an analysis.
 In a design situation, typically , several iterations are carries out before a final
design is frozen. Thus repeated 3-D analysis is can be very cumbersome.
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

5. APPROXIMATION OF GEOMETRY
AND FIELD VARIABLES
 A typical 2-D problem domain is shown in figure, a bracket with an internal
hole subjected to loads.
 The most common types of 2-D elements are triangle
and quadrilaterals as shown in figure.
 Each node is capable of independent motion along
the x and y axes and, typically, u and v as the
independent nodal degree of freedom(d.o.f) for plane
elasticity problems.
 There is only one temperature d.o.f. for 2-D heat
transfer problems.
 Simple lower order elements have straight side and
nodes only at the vertices.
 More complex higher order element permit curved
edges and mid-side or even internal nodes
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
Bracket with an internal hole

6.  Each element has one d.o.f (viz., temperature T)
When applied to heat transfer problems.
 Two displacement, u, v along the coordinate
axis for structural mechanics problems.
 The flow of an ideal fluid in 2d can be
represented in terms of a scalar potential
function and so we have only one d.o.f
per node.
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
2 5
1 4
2
5
3
6
1
1
2
4
3
8
2
7 3
1
4
3
Typical 2-D finite elements
6

7. THREE-NODED TRIANGULAR
ELEMENT
 The typical three-noded triangular element shown in figure.
 It has straight sides and three nodes, one at
each vertex.
 The nodes have co-ordinates (x1,y1), (x2,y2), (x3,y3)
in the global Cartesian co-ordinate frame OXY
as shown in the figure.
 Each node has just temperature d.o.f, T or two
d.o.f., viz, u and v, the translations along global
 X and Y axes, repectively.
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
u2
1
x1,y1
vi
3
x3,y3
2
x2, y2
u1
u3
v2
v3
X
Y
Simple three-noded triangle element
O

8.  Assume that the temperature field over the element is given by,
T(x,y) = c0 + c1x + c2y ----------------- (1)
 Considering that this expression should reduce to the nodal
temperature at the nodal points, we have
 T1= c0 + c1x1 + c2y1, T2= c0 + c1x2 + c2y2, T3= c0 + c1x3 + c2y3
 Solving for c0 , c1 , c2 we get
-1
c0 1 x1 y1 T1
c1 = 1 x2 y2 T2 ------------------- (2)
c2 1 x3 y3 T3
The shape function Ni = (1/2∆ ) { αi + βix + γiy}, i = 1,2,3Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

9. u1
v1
u N1 0 N2 0 N3 0 u2
 Displacement function u= = 0 N1 0 N2 0 N3 v2
v u3
v3
 We observe that this element may only permit a linear variation of the
unknown field variable within the element and thus derivatives such as
strains and heat flux will be constant throughout the element. In
structural mechanics, this element is therefore popularly known as the
Constant Strain Triangle (CST).Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

10. DERIVATION OF STIFFNESS MATRIX
FOR 2-D ELEMENT (CST ELEMENT)
 We know that stiffness matrix [K] for any element,
 Stiffness matrix, [K] = [B]T
[D] [B] dv
v
= [B]T
[D] [B] v [ dv = v]
v
= [B]T
[D] [B] A x t [ v = A x t]
Stiffness matrix, [K] = [B]T
[D] [B] A x t
[t = Thickness of elements]
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

11. 1 x1 y1
 Area of element A = (1/2) 1 x2 y2
1 x3 y3
β1 0 β2 0 β3 0
Strain displacement matrix, [B] = (1/2A) 0 γ1 0 γ2 0 γ3
γ1 β1 γ2 β2 γ3 β3
 Where β1 = y2 –y3
β2 = y3 –y1
β3 = y1 –y2
γ1 = x3 – x2
γ2 = x1 – x3
γ3 = x2– x1
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

12.  For plane stress problem,
1 v 0
[D] = E/(1-v2
) v 1 0
0 0 (1-v)/2
 For plane strain problem,
1-v v 0
[D] = E/(1+v)(1-2v) v 1-v 0
0 0 (1-2v)/2
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

13.  P1: For a triangular element shown in figure. Obtain the strain-
displacement relation matrix [B] and determine the strains ex, ey andγxy.
Nodal displacements are:
 u1 = 0.001; v2 = -0.004
 u2 = 0.003; v2 = 0.002
 u3 = -0.002; v3 = 0.005
 All co-ordinates are mm.
 Solution:
 x1 = 1mm ; y1 = 1mm
 x2 = 8mm; y2 = 4mm
 x3 = 2mm; y3 = 7mm
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
1
(1,1)
3
(2,7)
2
(8,4)
X
Y
O

14.  To find the element strain,
 Normal strain, ex
 Normal strain, ey
 Shear strain, γxy
1 x1 y1 1 1 1
 Area of element A = (1/2) 1 x2 y2 = (1/2) 1 8 4
1 x3 y3 1 2 7
= (1/2) [1x (56-8) – 1(7-4) + 1 (2-8)]
A = 19.5 mm
We know that, β1 0 β2 0 β3 0
Strain displacement matrix, [B] = (1/2A) 0 γ1 0 γ2 0 γ3 ----- (1)
γ1 β1 γ2 β2 γ3 β3
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

15.  β1 = y2 –y3 = 4-7 =-3
 β2 = y3 –y1 = 7-1 = 6
 β3 = y1 –y2 = 1-4 =-3
 γ1 = x3 – x2 = 2-8 = -6
 γ2 = x1 – x3 = 1-2 = -1
 γ3 = x2– x1 = 8-1 = -7
 Substituting the above values in equ 1.
-3 0 6 0 -3 0
 [B] = (1/2x 19.5) 0 -6 0 -1 0 7
-6 -3 -1 6 7 -3
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

16.  We know that,
u1
v1
 Elemental strain, {e} = [B] {u} = [B] u2
v2
u3
v3
0.001
-0.004
-3 0 6 0 -3 0 0.003
 {e} = (1/39) 0 -6 0 -1 0 7 0.002
-6 -3 -1 6 7 -3 -0.002
0.005
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

17. 0.021
 {e} = 1/39 0.057
-0.014
ex 5.38 x 10-4
=> ey = 1.4615 x 10-3
τxy 3.589 x 10-4
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

18.  P2: Determine the shape functions N1, N2 and N3 at the interior point ‘P’ for
the triangular element shown in figure.
Given :
x1 = 3 y1 = 4
x2 = 8 y2 = 5
x3 = 5 y3 = 8
x = 4.5 y = 6
Solution:
We know that,
x = (x1-x3) N1 + (x2-x3) N2 + x3 --- (1)
y = (y1-y3) N1 + (y2-y3) N2 + y3 --- (2)
Substitute the co-ordinate values in the above equations,
and also we know that,
N1 + N2 + N3 = 1 --- (3)
N1 = 0.4166, N2 = 0.1111 and N3 = 0.4723
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
1
(3,4)
P
(4.5, 6)
3
(5,6)
2
(8,5)
X
Y
O

19. FOUR-NODED RECTANGULAR
ELEMENT
 A typical element is shown in figure. It is rectangular and has four
nodes, one at each vertex. The nodes have coordinates (X1,Y1), (X2,Y2),
(X3,Y3), and (X4,Y4), in the global Cartesian coordinates frame (OXY) as
shown in figure.
(i) Displacement field and shape function:
N1 = 1- (x/L) – (y/H) + (xy/LH)
N2 = (x/L) – (xy/LH)
N3 = xy/LH
N4 = (y/H) – (xy/LH)
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
X
Y
O
x
y
2
1
4 3
L
H
A Four noded Rectangular Element
0

20.  If this element is used to model structural mechanics problems, each node will
have two d. o. f., viz., u and v and to write the displacements at any interior point
in terms of the nodal displacements using the same shape functions as follows:
u1
v1
u N1 0 N2 0 N3 0 N4 0 u2
= 0 N1 0 N2 0 N3 0 N4 v2
v u3
v3
u4
v4
This element permits a linear variation of unknown field variable along x =
constant or y= constant lines, and thus it is known as the Bilinear Element. Strain
and heat flow flux are not necessarily constant within the element.Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

21.  P1: For a noded rectangular element shown in figure, determine the
temperature at the point (2,1).The nodal temperatures are T1 = 420
C,
T2 = 540
C, T3 = 560
C and T4 = 460
C.
 Solution:
 The variation of temperature T on the element
can be expressed as
 T = N1T1 + N2T2 + N3T3 + N4T4
 Now the shape functions are
N1 = 1- (x/L) – (y/H) + (xy/LH); N3 = xy/LH
N2 = (x/L) – (xy/LH); N4 = (y/H) – (xy/LH)
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
x
y
2
1
4 3
(3, 0)
A Four noded Rectangular Element
(0, 0)
(3, 2)(0, 2)

22. and the nodal temperatures are
 T1 = 420
C, T2 = 540
C, T3 = 560
C and T4 = 460
C.
 From the figure, we know that
 L = x2 – x1 = 3 – 0 = 3 and H = y4 – y1 = 2 - 0 = 2
 Substituting the values of nodal temperature in the shape function
equations, we get the shape functions for the point P (2, 1)
 N1 = 1- (x/L) – (y/H) + (xy/LH) = 1- (2/3) – (1/2) + (2/6) = 1/6
 N2 = (x/L) – (xy/LH) = (2/3) – (2/6) = 1/3
 N3 = xy/LH = 2/6 =1/3
 N4 = (y/H) – (xy/LH) = (1/2) – (2/6) = 1/6
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

23.  Now, the temperature a the point (2, 1) is give by
 T = N1T1 + N2T2 + N3T3 + N4T4
 T = (1/6)x 42 + (1/3) x 54 + (1/3) x 56 + (1/6) x 46 = 51.40
C
T = 51.40
C
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

24. SIX NODED LINEAR STRAIN
TRIANGULAR (LST)ELEMENT
 A six noded triangular element is known as Linear Strain Triangular
(LST) element which is shown in figure.
 It has six nodes, three at the vertices and three on the edges.
 While usually the edge nodes are located at the mod-point, it is not
necessary.
 The nodes have coordinates (x1, y1), (x2, y2), …
(x6, y6) in the GCC frame OXY as shown in
the figure.
 Each node has just temperature d.o.f, T or two
d.o.f., viz, u and v, the translations along global
X and Y axes, repectively.
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
u2
1
x1,y1
vi
3
x3,y3
2
u1
u3
v2
v3
X
Y
Six-noded Linear triangle element
O
u5
v5
u4
v4
u6
v6
6
4
5
x2,y2

25.  Assume that the temperature field over the element
is given by,
T(x,y) = c0 + c1x + c2y + c3x2
+ c4xy + c5y2
----------------- (1)
 Considering that this expression should reduce to the nodal
temperature at the nodal points, we have
 T1 = c0 + c1x1 + c2y1+ c3x1
2
+ c4x1y1 + c5y1
2
 T2 = c0 + c1x2 + c2y2 + c3x2
2
+ c4x2y2 + c5y2
2
 T3 = c0 + c1x3 + c2y3 + c3x3
2
+ c4x3y3 + c5y3
2
 T4 = c0 + c1x4 + c2y4 + c3x4
2
+ c4x4y4 + c5y4
2
 T5 = c0 + c1x5 + c2y5 + c3x5
2
+ c4x5y5 + c5y5
2
 T6 = c0 + c1x6 + c2y6 + c3x6
2
+ c4x6y6 + c5y6
2
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

26. DIFFERENTIATE BETWEEN
CST & LST ELEMENTS
S.No CST Element LST Element
1. It is a two dimensional linear
element (i.e., Simplex element)
It is a two dimensional non-linear element
(i.e., Complex element)
2. It has only three primary nodes
at the corners
It has three primary nodes at the corners
and three secondary nodes at the midsides
3. The Strain is constant
throughout the element
The Strain is varying linearly inside the
element.
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

27. Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
S.No CST Element LST Element
4. The polynomial functions for
CST element are u= a1+a2x+a3y
v= a4+a5x+a6y
The polynomial functions for LST element
are
u= a1+a2x+a3y+a4x2
+a5xy+a6y2
v= a7+a8x+a9y+a10x2
+a11xy+a12y2
u2
1
x1,y1
vi
3
x3,y3
2
u1
u3
v2
v3
X
Y
Six-noded Linear triangle element
O
u5
v5
u4
v4
u6
v6
6
4
5
x2,y2
u2
1
x1,y1
vi
3
x3,y3
2
x2, y2
u1
u3
v2
v3
X
Y
Simple three-noded triangle element
O

28. TWO-DIMENSIONAL HEAT
TRANSFER
 The distribution of temperature(assuming a linear variation)
over the element.
 Assuming unit thickness of elemental volume can be represented
ass dv = dA. For an isotropic material kx = ky = k.
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
Edge Convection
Face
Convection

29.  Elemental stiffness matrix [k],
 [ke
] = [k1
e
] + [k2
e
] + [k3
e
]
Conduction Edge convection Face convection
 Conduction:
bi
2
+ ci
2
bibj+ cicj bibk+ cick
 [k1] = kt/4A bjbi+ cjci bj
2
+ cj
2
bjbk+ cjck
bkbi+ ckci bkbj+ ckcj bk
2
+ ck
2
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

30.  Edge Convection:
Edge ij :
2 1 0
 [k2 ] = (h Hij t) / 6 1 2 0
0 0 0
Edge Length:
Hij = √ (x1 – x2)2
+ (y1– y2)2
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
x2, y2
x1, y1
x3, y3
i
k
j
h

31. Edge jk :
0 0 0
 [k2 ] = (h Hjk t) / 6 0 2 1
0 1 2
Edge Length:
Hjk = √ (x2 – x3)2
+ (y2– y3)2
Where,
bi = yj – yk ci= xk – xj
bj = yk – yi cj= xi– xk
bk = yi – yj ck = xj – xiDr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

32. 1 x1 y1
 Area of triangle 2A = 1 x2 y2
1 x3 y3
Face Convection:
2 1 1
 [k3 ] = (h A) / 12 1 2 1
1 1 2
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
i
k
j
FaceConvection

33.  Force vector:
E
P = Σ P(e)
e
= P1
(e)
+ P2
(e)
+ P3
(e)
 Convection at edge:
1 i
P1 = (h T∞Hij t) / 2 1 j
0 k
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

34.  Force area Convection:
1 i
P2 = (h T∞A) / 3 1 j
1 k
 Internal Heat Source:
1 i
P3 = (Q tA) / 3 1 j
1 k
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

35.  General FE representation is
bi
2
+ ci
2
bibj+ cicj bibk+ cick 2 1 0
 [k1]=kt/4A bjbi+ cjci bj
2
+ cj
2
bjbk+ cjck +(h Hij t)/6 1 2 0
bkbi+ ckci bkbj+ ckcj bk
2
+ ck
2
0 0 0
2 1 1 1 i 1
+(h Hij t)/6 1 2 1 = (h T∞Hij t) / 2 1 j + (h T∞A) / 3 1
1 1 2 0 k 1
1
+ (Q t A)/3 1
[Assume t=1 unit in problems] 1Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

36. P1:Compute the element matrices and vectors for the element shown
in figure, when the edges jk and ki experience convection heat
loss.
 Qo = 50 W/cm2
 K = 60 W /cm o
k
 h = 10 W/cm20
k Edge kj
 T∞ = 400
C
 h = 15 W/cm20
k Edge ik
 T∞ = 400
C
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.
(4, 6)
(8, 10)
i
j
k
(12, 8)

37. bi = yj – yk = 2 ci= xk – xj = 4
bj = yk – yi = 2 cj= xi– xk = -8
bk = yi – yj= -4 ck = xj – xi = 4
1 4 6
2A = 1 12 8 => 1(120-64)-4(2)+6(8-12)= 24
1 8 10
A = 12
Hik = √ (x1 – x3)2
+ (y1– y3)2
= √(4-12)2
+ (6-8)2
= 8.246
Hkj = √ (x2– x3)2
+ (y2– y3)2
= √(12-8)2
+ (8-10)2
= 4.47Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

38.  General FE equation for elemental evaluation:
 Conduction:
bi
2
+ ci
2
bibj+ cicj bibk+ cick 25 -35 10
 [k1] = kt/4A bjbi+ cjci bj
2
+ cj
2
bjbk+ cjck = -35 85 -50
bkbi+ ckci bkbj+ ckcj bk
2
+ ck
2
10 -50 40
 Edge Convection:
2 0 1 0 0 0
 [k1] = (hikHik)/6 0 0 0 + (hkjHkj)/6 0 2 1
1 0 2 0 1 2
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

39. 2 0 1 0 0 0
 [k2]=(15x8.25)/6 0 0 0 + (10x4.47)/6 0 2 1
1 0 2 0 1 2
41.25 0 20.625
[k2] = 0 14.9 7.45
20.625 7.45 56.15
Face Convection:
[k2] = 0 (No face convection)
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

40.  Force vector calculation:
 P = P1
(e)
+ P2
(e)
+ P3
(e)
 Convection at edges:
1 i 0
[P1] = (hikT∞Hik) /2 0 j + (hkjT∞Hkj) /2 1
1 k 1
2475
[P1] = 894
3369
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

41.  [P2] = 0 (No face convection)
1
 [P3] = (Q tA) / 3 1
1
200
 [P3] = 200
200
2675
 P = P1
(e)
+ P2
(e)
+ P3
(e)
= 1094
3569
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.

42.  The general FE representation is given as,
66.25 -35 30.625 T1 2675
 [k] {T} = {P}=> -35 99.9 -42.55 T2 = 1094
30.625 -42.55 96.15 T3 3569
Dr.G.PAULRAJ,
Professor&Head(Mech.),
VTRS,Avadi,Chennai.