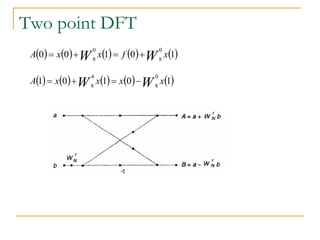
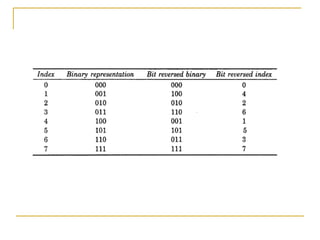
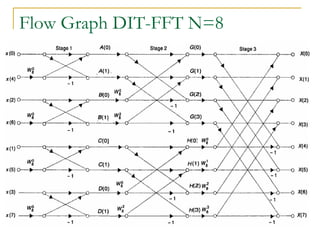
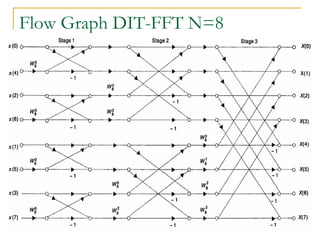
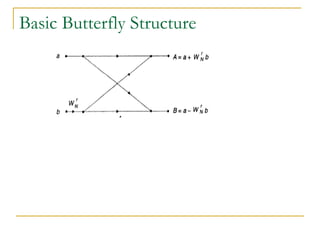
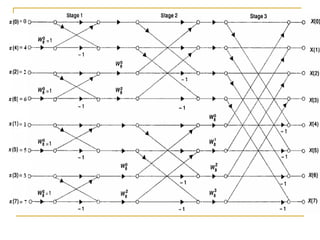
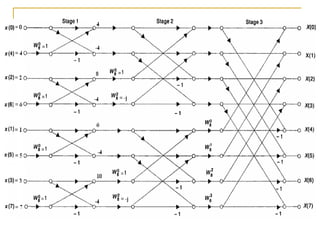
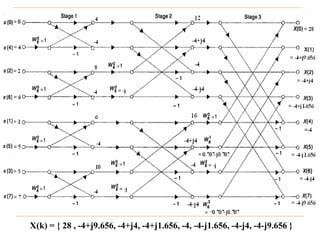
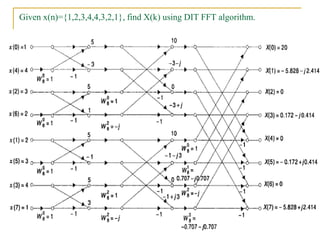
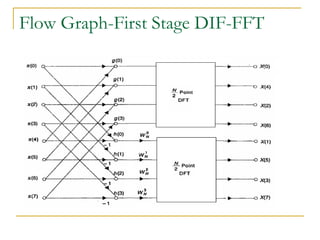
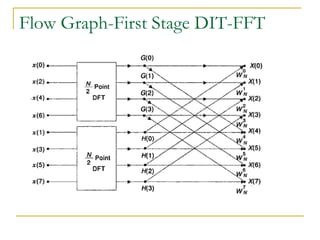
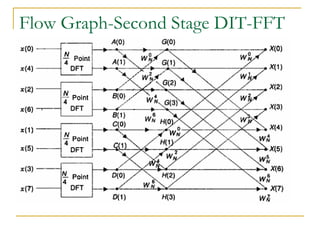
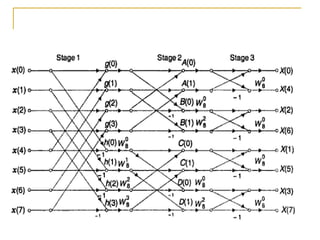
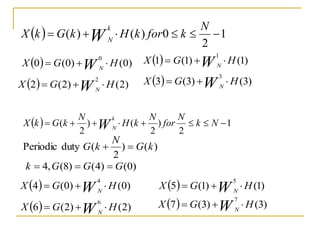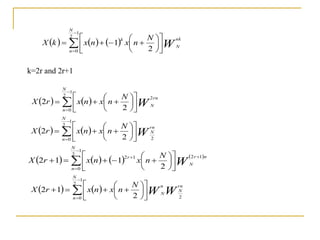The document discusses the Fast Fourier Transform (FFT), an efficient algorithm for computing the Discrete Fourier Transform (DFT). It details the Radix-2 FFT algorithm, including direct computation through decimation in time (DIT) and decimation in frequency (DIF). The document includes mathematical formulations and examples to illustrate how the FFT transforms input signals.

1. FAST FOURIER TRANSFORM
(FFT)
P.ANBARASAN
ASST. PROFESSOR/ EEE DEPT

2. FFT
 The FFT is an algorithm that efficiently computes the discrete
Fourier transform (DFT)
    N
nk
j
N
n
e
n
x
k
X /
2
1
0






k = 0 to N-1
N
nk
j
nk
N
e
W
/
2


   W
nk
N
N
n
n
x
k
X 



1
0
k = 0 to N-1
Twiddle Factor

3. FFT
 Radix-2 FFT Algorithm
Basic DFT is of size 2
The N point DFT is decimated into 2 point DFT
1. Decimation in Time (DIT) Algorithm
2. Decimation in Frequency (DIF) Algorithm
L
r
N 

4. Decimation in Time (DIT-FFT)
Breaking x(n) in to its even and odd numbered values,
   W
nk
N
N
n
n
x
k
X 



1
0
     W
W
nk
N
N
odd
n
n
nk
N
N
even
n
n
n
x
n
x
k
X 









1
,
0
1
,
0
Substitute n=2r for n even and n=2r+1 for n odd, we have
       
W
W
k
r
N
N
r
rk
N
N
r
r
x
r
x
k
X
1
2
1
2
0
2
1
2
0
1
2
2






 


       rk
N
N
r
k
N
rk
N
N
r
W
W
W r
x
r
x
k
X
2
1
2
0
2
1
2
0
1
2
2 









5.        rk
N
N
r
k
N
rk
N
N
r
W
W
W r
x
r
x
k
X
2
1
2
0
2
1
2
0
1
2
2 








W
W N
N
j
N
j
N
e
e
1
2
2
)
1
(
2
)
2
(
2
2







     W
W
W
rk
N
N
r
k
N
rk
N
N
r
r
x
r
x
k
X
2
1
2
0
2
1
2
0
1
2
2 








  )
(
)
( k
H
k
G
k
X W
k
N


 1
2
.....
2
,
1
,
0
, 

N
k
 



























1
2
)
2
(
)
2
(
1
2
0
)
(
)
(
2 N
k
N
for
N
k
H
N
k
G
N
k
for
k
H
k
G
k
X
W
W
N
k
N
k
N

6.   )
0
(
)
0
(
0
0
H
G
X W N


   )
1
(
)
1
(
1
1
H
G
X W N



  )
2
(
)
2
(
2
2
H
G
X W N


   )
3
(
)
3
(
3
3
H
G
X W N



  1
2
0
)
(
)
( 





N
k
for
k
H
k
G
k
X W
k
N
  1
2
)
2
(
)
2
( 






 N
k
N
for
N
k
H
N
k
G
k
X W
k
N
)
0
(
)
4
(
)
8
(
,
4 G
G
G
k 


)
(
)
2
(
duty
Periodic k
G
N
k
G 

  )
0
(
)
0
(
4
4
H
G
X W N


   )
1
(
)
1
(
5
5
H
G
X W N



  )
2
(
)
2
(
6
6
H
G
X W N


   )
3
(
)
3
(
7
7
H
G
X W N




7. Using Symmetry property
W
W
k
N
N
k
N



2
  )
0
(
)
0
(
4
0
H
G
X W N


   )
1
(
)
1
(
5
1
H
G
X W N



  )
2
(
)
2
(
6
2
H
G
X W N


   )
3
(
)
3
(
7
3
H
G
X W N




8. 4 Point DFT
     
k
B
k
A
k
G W
k
N
2


   W
rk
N
N
r
r
g
k
G
2
1
2
0




     W
W
k
l
N
N
l
lk
N
N
l
l
g
l
g
k
G
)
1
2
(
2
1
4
0
2
2
1
4
0
1
2
2






 


     W
W
W
rk
N
N
r
k
N
rk
N
N
r
r
x
r
x
k
X
2
1
2
0
2
1
2
0
1
2
2 








     W
W
W
lk
N
N
l
k
N
lk
N
N
l
l
g
l
g
k
G
4
1
4
0
2
4
1
4
0
1
2
2 








      W
W
W
k
N
lk
N
N
l
lk
N
N
l
l
g
l
g
k
G
2
2
2
1
4
0
2
2
1
4
0
1
2
2 









9. 4 Point DFT
     W
W
W
lk
N
N
l
lk
N
lk
N
N
l
l
h
l
h
k
H
4
1
4
0
2
4
1
4
0
1
2
2 








Similarly,
     
k
D
k
C
k
H W
k
N
2


     
k
B
k
A
k
G W
k
N
2


         
0
0
0
0
0
0
0
2
B
A
B
A
G W
W N
N 



         
1
1
1
1
1
2
1
2
B
A
B
A
G W
W N
N 



             
0
0
2
2
2
2
2
0
4
2
2
B
A
B
A
B
A
G W
W
W N
N
N 





             
1
1
3
3
3
3
3
2
6
3
2
B
A
B
A
B
A
G W
W
W N
N
N 






10.      
k
D
k
C
k
H W
k
N
2


         
0
0
0
0
0
0
0
2
D
C
D
C
H W
W N
N 



         
1
1
1
1
1
2
1
2
D
C
D
C
H W
W N
N 



             
0
0
2
2
2
2
2
0
4
2
2
D
C
D
C
D
C
H W
W
W N
N
N 





             
1
1
3
3
3
3
3
2
6
3
2
D
C
D
C
D
C
H W
W
W N
N
N 






11. Two point DFT
         
1
0
1
0
0
0
8
0
8
x
f
x
x
A W
W 



         
1
0
1
0
1
0
8
4
8
x
x
x
x
A W
W 




13. Flow Graph DIT-FFT N=8

14. Flow Graph DIT-FFT N=8

15. Basic Butterfly Structure

16. Given x(n)={0,1,2,3,4,5,6,7}, find X(k)
using DIT FFT algorithm.
N
nk
j
nk
N
e
W

2


1
0

W N
707
.
0
707
.
0
1
j
W N


j
W N


2
707
.
0
707
.
0
3
j
W N




20. X(k) = { 28 , -4+j9.656, -4+j4, -4+j1.656, -4, -4-j1.656, -4-j4, -4-j9.656 }

21. Given x(n)={1,2,3,4,4,3,2,1}, find X(k) using DIT FFT algorithm.

22. Decimation in Frequency (DIF-FFT)
   W
nk
N
N
n
n
x
k
X 



1
0
     W
W
nk
N
N
N
n
nk
N
N
n
n
x
n
x
k
X 







1
2
1
2
0
    W
W
k
N
n
N
N
n
nk
N
N
n
N
n
x
n
x
k
X












 







 2
1
2
0
1
2
0 2
     
W
W
W
nk
N
N
n
k
N
N
nk
N
N
n
N
n
x
n
x
k
X 














1
2
0
2
1
2
0 2
 k
k
j
k
k
j
N
Nk
j
k
N
N
e
e
W
1
)
sin(
)
cos(
2
2
2
2







 



      W
W
nk
N
N
n
k
nk
N
N
n
N
n
x
n
x
k
X 















1
2
0
1
2
0 2
1

23.       W
nk
N
N
n
k N
n
x
n
x
k
X 


















1
2
0 2
1
k=2r and 2r+1
    W
rn
N
N
n
N
n
x
n
x
r
X
2
1
2
0 2
2 

















    W
rn
N
N
n
N
n
x
n
x
r
X
2
1
2
0 2
2 

















       
W
n
r
N
N
n
r N
n
x
n
x
r
X
1
2
1
2
0
1
2
2
1
1
2




 
















    W
W
rn
N
n
N
N
n
N
n
x
n
x
r
X
2
1
2
0 2
1
2 



















24.     W
rn
N
N
n
N
n
x
n
x
r
X
2
1
2
0 2
2 
















     W
W
rn
N
n
N
N
n
N
n
x
n
x
r
X
2
1
2
0 2
1
2 


















    








2
N
n
x
n
x
n
g     








2
N
n
x
n
x
n
h
     
4
0
0 x
x
g 

     
5
1
1 x
x
g 

     
6
2
2 x
x
g 

     
7
3
3 x
x
g 

     
4
0
0 x
x
h 

     
5
1
1 x
x
h 

     
6
2
2 x
x
h 

     
7
3
3 x
x
h 

Where

25. Flow Graph-First Stage DIF-FFT

26.     W
N
n
x
n
x
r
X rn
N
N
n
2
1
2
0 2
2  
















    








2
N
n
x
n
x
n
g
     W
n
g
W
n
g
r
X rn
N
N
N
n
rn
N
N
n
2
1
2
4
2
1
4
0
2 







   W
n
g
r
X rn
N
N
n
2
1
2
0
2 



Where
    rn
N
N
N
r
N
N
n
W
N
n
g
W
n
g
r
X 2
1
4
0
4
2
1
4
0 2
.
2










 


















1
2 

N
N
W
      rn
N
r
N
n
W
N
n
g
n
g
r
X 2
1
4
0 2
.
1
2
























27.     ln
4
1
4
0 4
4 N
N
n
W
N
n
g
n
g
l
X






















      rn
N
r
N
n
W
N
n
g
n
g
r
X 2
1
4
0 2
.
1
2























     
1
2
2
1
4
0 2
.
2
4 

 



















 l
n
N
N
n
W
N
n
g
n
g
l
X
    ln
4
1
4
0
4 N
N
n
W
n
A
l
X














     
1
2
2
1
4
0
2
4 

 











 l
n
N
N
n
W
n
B
l
X
     
2
0
0 g
g
A 

     
3
1
1 g
g
A 

     
2
0
0 g
g
B 

     
3
1
1 g
g
B 


29. Flow Graph-First Stage DIT-FFT

30. Flow Graph-Second Stage DIT-FFT